每日OJ题_路径dp⑥_力扣174. 地下城游戏

本文主要是介绍每日OJ题_路径dp⑥_力扣174. 地下城游戏，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

力扣174. 地下城游戏

解析代码

---

力扣174. 地下城游戏

174. 地下城游戏

难度 困难

恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里，他必须穿过地下城并通过对抗恶魔来拯救公主。

骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下，他会立即死亡。

有些房间由恶魔守卫，因此骑士在进入这些房间时会失去健康点数（若房间里的值为负整数，则表示骑士将损失健康点数）；其他房间要么是空的（房间里的值为 0），要么包含增加骑士健康点数的魔法球（若房间里的值为正整数，则表示骑士将增加健康点数）。

为了尽快解救公主，骑士决定每次只 向右 或 向下 移动一步。

返回确保骑士能够拯救到公主所需的最低初始健康点数。

注意：任何房间都可能对骑士的健康点数造成威胁，也可能增加骑士的健康点数，包括骑士进入的左上角房间以及公主被监禁的右下角房间。

示例 1：

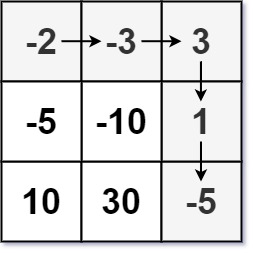
输入：dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
输出：7
解释：如果骑士遵循最佳路径：右 -> 右 -> 下 -> 下 ，则骑士的初始健康点数至少为 7 。

示例 2：

输入：dungeon = [[0]]
输出：1

提示：

• m == dungeon.length
• n == dungeon[i].length
• 1 <= m, n <= 200
• -1000 <= dungeon[i][j] <= 1000

class Solution {
public:int calculateMinimumHP(vector<vector<int>>& dungeon) {}
};

---

解析代码

        路径dp问题，这道题的状态表示如果定义成：从起点开始，到达 [i, j] 位置的时候，所需的最低初始健康点数。 那么分析状态转移方程的时候会有一个问题：那就是当前的健康点数还会受到后面的路径的影响。也就是从上往下的状态转移不能很好地解决问题。

        这个时候我们要换⼀种状态表示：从 [i, j] 位置出发，到达终点时所需要的最低初始健康点 数。这样在分析状态转移的时候，后续的最佳状态就已经知晓。

综上所述， dp[i][j] 表示：从 [i, j] 位置出发，到达终点时所需的最低初始健康点数。

---

状态转移方程：

dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];

        如果当前位置的 dungeon[i][j] 是⼀个比较大的正数的话， dp[i][j] 的值可能变 成 0 或者负数。也就是最低点数会小于 1 ，那么骑士就会死亡。因此求出来的 dp[i] [j] 如果小于等于 0 的话，说明此时的最低初始值应该为 1 。

---

初始化和返回值：

        在本题中，在 dp 表最后面添加一行，并且添加一列后，所有的值都先初始化为INT_MAX，然后让 dp[m][n - 1] = dp[m - 1][n] = 1 即可。

从右下往左上填值，最后返回 dp[0][0] 的值。

class Solution {
public:int calculateMinimumHP(vector<vector<int>>& dungeon) {int m = dungeon.size(), n = dungeon[0].size();// dp[i][j] 表示：从 [i, j] 位置出发，到达终点时所需的最低初始健康点数vector<vector<int>> dp(m+1, vector<int>(n+1, INT_MAX)); // 多开一行一列dp[m][n-1] = dp[m-1][n] = 1;for(int i = m-1; i >= 0; --i){for(int j = n-1; j >= 0; --j){dp[i][j] = min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j];if(dp[i][j] < 1)dp[i][j] = 1;}}return dp[0][0];}
};

这篇关于每日OJ题_路径dp⑥_力扣174. 地下城游戏的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---