本文主要是介绍数据结构与算法第三套试卷小题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.删除链表节点
**分析:**首先用指针变量q指向结点A的后继结点B,然后将结点B的值复制到结点A中,最后删除结点B。

2.时间复杂度的计算
**分析:**当涉及嵌套循环的时候,我们可以直接分析内层循环即可,看内层循环走了多少次

3.堆排序以及与其他排序的区别:
A

解析:
问的是空间复杂度,堆排序的空间复杂度为0(1);
时间复杂度为0(nlogn);
思路:
分为创建堆和调整堆——>每调整一次的时间复杂度为0(logn),一共需要调整n-1次
其他:
1.选择排序: 时间复杂度无论最好和最坏和平均都为0(n^2);
在空间复杂度上与冒泡排序,插入排序,选择排序类似都为0(1);
2.快速排序: 时间复杂度为0(nlogn),最坏为0(n^2);空间复杂度为0(1)
3.归并排序: 时间复杂度均为0(nlogn),空间复杂度为0(n);
重点区别:

快速排序、归并排序和插入排序必须等到整个排序结束后才能够求出最小的10个数,而堆排序只需要在初始堆的基础上再进行10次筛选即可,每次筛选的时间复杂度为O(log2n)
4.快速排序的思路:

方法论:
从两头往中间搜索,右边找小,左边找大,右边先走
**1.第一步:**右边找到了10,左边找到了21,交换
**2.第二步:**在上面的位置上,右边继续向前,遇到了上一步的10,左右相遇,所以10的位置就是20的基准位,结束
5.有向无向图和邻接表的转换
1:无向图的表头节点数,表节点数:顶点个数,边2;
2:有向图的表头节点数,表节点数:顶点个数,边1;
6.强连通图
1.首先它的本质只是一个连通图,任意两个顶点之间都存在一条有向路径,即从任意一个顶点出发可以到达图中的任意其他顶点。
2.有向完全图一定是强连通,反之不一定;
3.最少边为n=顶点数
7.数据结构
1.数据结构的物理结构主要包括: 顺序存储结构,链式存储结构;
2.数据结构的逻辑结构: 线性结构,非线性结构(线性结构有线性表和栈,队列;非线性结构有树,图结构);
3.存储结构分为: 顺序存储,链式存储,索引存储,散列存储;
4.基本概念:
1.数据的基本单位是数据元素;
2.数据元素最小单位为数据项;
3.具有相同性质的数据元素的集合为数据对象;
4.数据对象的集合为数据类型
5.存储结构和逻辑结构的关系:
存储结构则决定了数据在计算机内存中的实际存储方式;
逻辑结构描述了数据元素之间的关系;
数据结构是由其逻辑结构和存储结构共同决定的;
8.算法的特性:
五大特性: 有穷性,确定性,可行性,输入,输出;
9.树
1.深度: log2(n)+1 【n为顶点数】
**2.空指针域:**知道有多少叶子节点即可,然后利用n=n0+n1+n2,n2=n0-1;
10.图
出度: 顶点i在邻接矩阵上第i行的所有元素之和为出度;
入度: 顶点i在邻接矩阵上第i列上所有元素之和为入度;
邻接表上,顶点有n个,表头节点就有n个,至于表节点对应的是图某顶点的出度;
11.哈夫曼树

1.如何绘制: 两个最小生成树合并为一个新的树,然后重复以往过程;
2.情况: 哈夫曼树首先分为叶子节点和非叶子节点,叶子节点的度为1,非叶子节点的度为2;
所以度为1的节点一定为叶子节点,而哈夫曼树的构造后,叶子节点数一定为0——>所以度为1的节点数即为0;
12.二分查找最多次数:

log2n+1;
13.数据结构增删改查操作的时间复杂度
1.队列(Queue):
增加元素(enqueue):O(1)
删除元素(dequeue):O(1)
修改元素:队列通常不支持直接修改元素
查找元素:通常需要遍历整个队列,时间复杂度为O(n)
2.栈(Stack):
增加元素(push):O(1)
删除元素(pop):O(1)
修改元素:栈通常不支持直接修改元素
查找元素:通常需要遍历整个栈,时间复杂度为O(n)
3.树(Tree):
增加元素:O(log n) - 平衡二叉搜索树的情况下,最好为O(log n),最坏为O(n)
删除元素:O(log n) - 平衡二叉搜索树的情况下,最好为O(log n),最坏为O(n)
修改元素:可以视为删除+增加操作,时间复杂度与删除和增加相同
查找元素:O(log n) - 平衡二叉搜索树的情况下,最好为O(log n),最坏为O(n)
4.图(Graph):
增加元素(添加节点或边):O(1) - 在邻接表中添加节点或边的时间复杂度为O(1)
删除元素(删除节点或边):O(degree) - 对于邻接表,删除节点或边的时间复杂度取决于该节点的度数
修改元素:通常需要进行删除和增加操作,时间复杂度与删除和增加相关
查找元素:通常需要遍历整个图,时间复杂度为O(V+E),其中V为节点数,E为边数
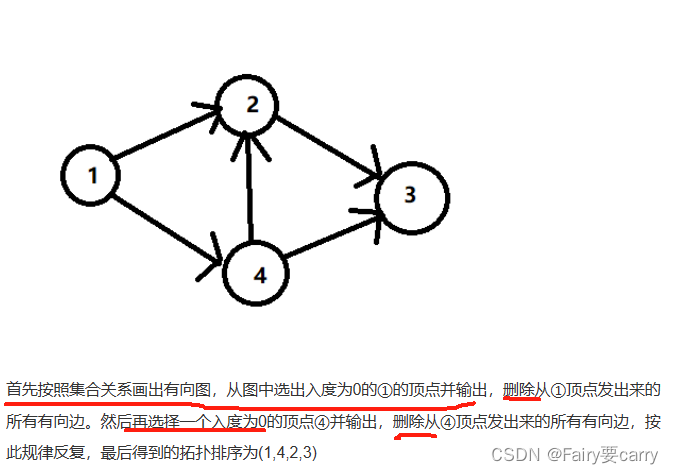
14.求图的拓扑序列:
总结: 1.首先画出给定边集合的有向图,2.然后删除入度为0的节点,并去除它的出度边
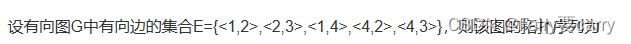
这篇关于数据结构与算法第三套试卷小题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








