本文主要是介绍求递归算法时间复杂性,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
节点的单一子问题代价:函数执行过程中,除去递归调用以外的代价
递推方法
求n!的递归算法:
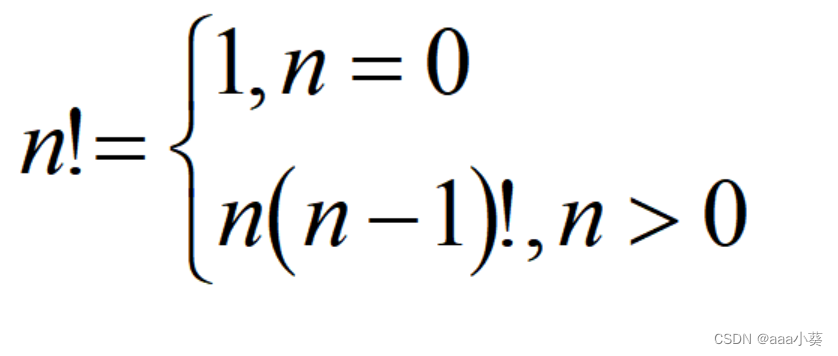
该算法的时间复杂性: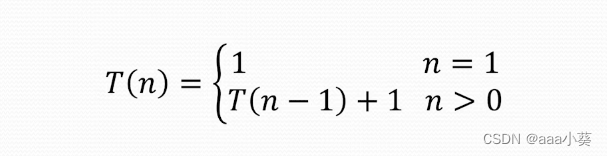
递推过程:
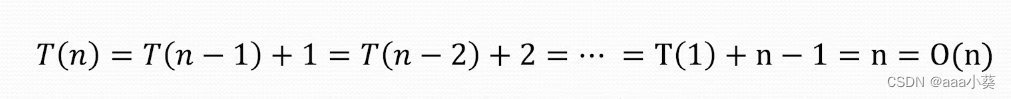
主定理方法
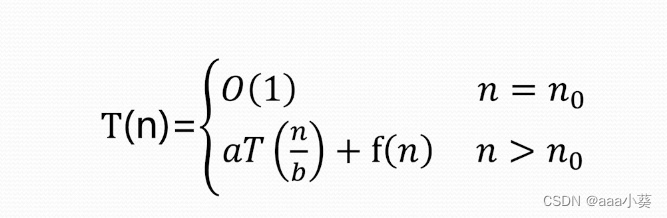
要求:a>=1,b>1
求解步骤:
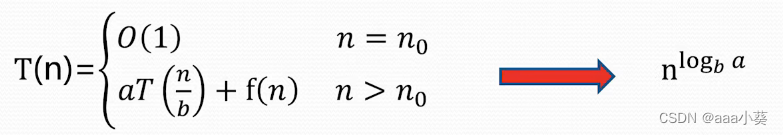

f(n)的渐进上界是以n的log以b为底的e次幂
判断关系后一定要满足这三个对应规则
例题:
规则一:棋盘覆盖的时间复杂性

规则二:归并排序的时间复杂性

规则三:时间复杂性的递归定义

递归树方法
定义:对一个时间复杂性的算法进行迭代计算,然后求和
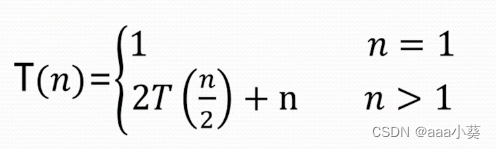
2表示我们将一个问题分解为 2 个子问题
n/2表示每个子问题的规模是原问题的 1/2
n表示合并需要的额外计算时间
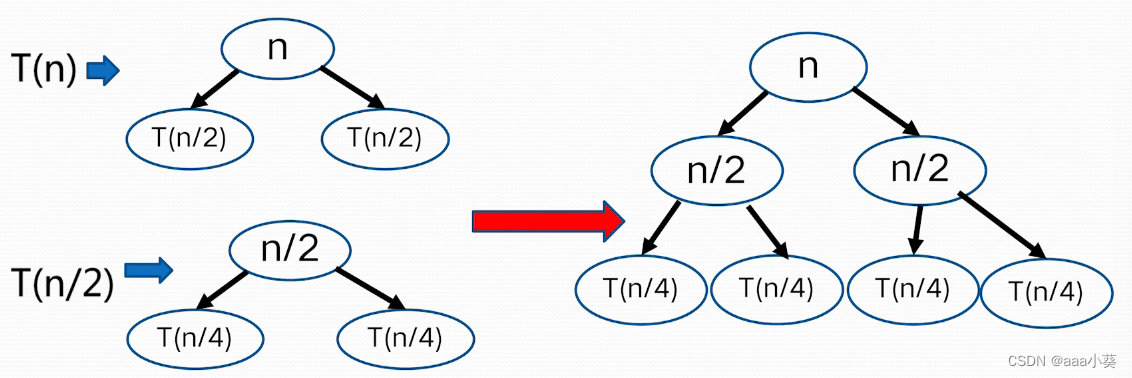
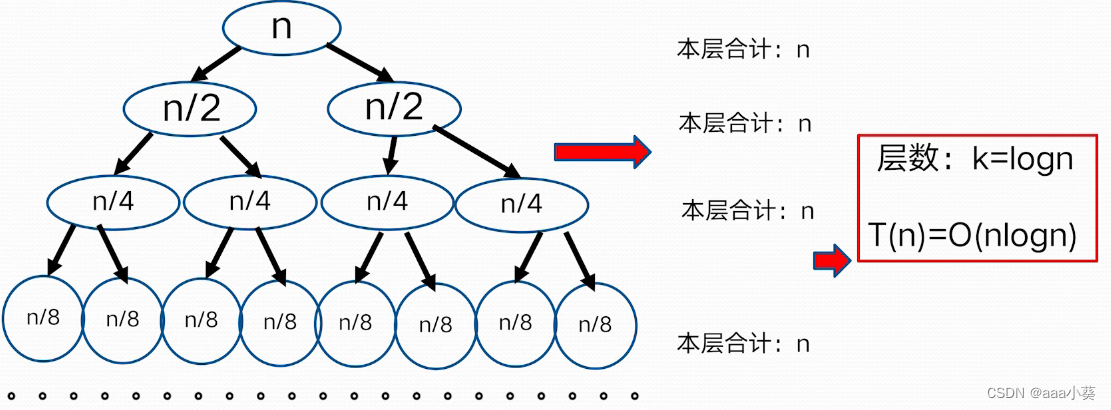
f(n)作为树的根节点,每一个子问题放在分支上
树中所有的值相加 = 算法时间复杂性
最后一层全都=1,假设一共k层,k=logn
这篇关于求递归算法时间复杂性的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




