本文主要是介绍【神经网络与深度学习】深度神经网络(DNN),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
概述
深度神经网络(Deep Neural Networks,DNN)是一种由多个隐藏层组成的神经网络模型。每个隐藏层由多个神经元组成,这些神经元通过权重和激活函数进行信息传递和计算。
深度神经网络通过多层的非线性变换,可以学习到更加抽象和复杂的特征表示。每一层都可以将输入数据转化为更高级的表示,从而更好地捕捉数据的特征和模式。通过不断叠加隐藏层,网络可以逐渐学习到更多的抽象特征,提高模型的表达能力。
深度神经网络在诸多领域中取得了重大突破和成功应用,如图像识别、语音识别、自然语言处理等。它能够处理大规模的数据,并具有强大的表示学习能力,能够自动提取和学习数据中的关键特征,从而实现更高水平的模式识别和预测能力。
然而,深度神经网络的训练也面临一些挑战,如梯度消失或梯度爆炸问题以及过拟合等。为了克服这些问题,出现了一些改进的深度神经网络结构和训练技巧,如卷积神经网络(CNN)、循环神经网络(RNN)、残差网络(ResNet)等。这些创新不断推动着深度神经网络的发展,并在各种领域中发挥着重要作用。
结构
神经网络层
首先通过图片来观察神经网络层的结构,第一张图是浅层神经网络,包括一个输入层,一个隐藏层和一个输出层。
- 输入层:它所包含的神经元的个数等于单个实例所包含的特征数。只负责输入数据,没有激活函数。
- 隐藏层:作用是提取特征,必须包含激活函数。
- 输出层:它所包含的神经元的数目与标签的类别数有关,主要负责输出模型的预测值,它可以包含激活函数。

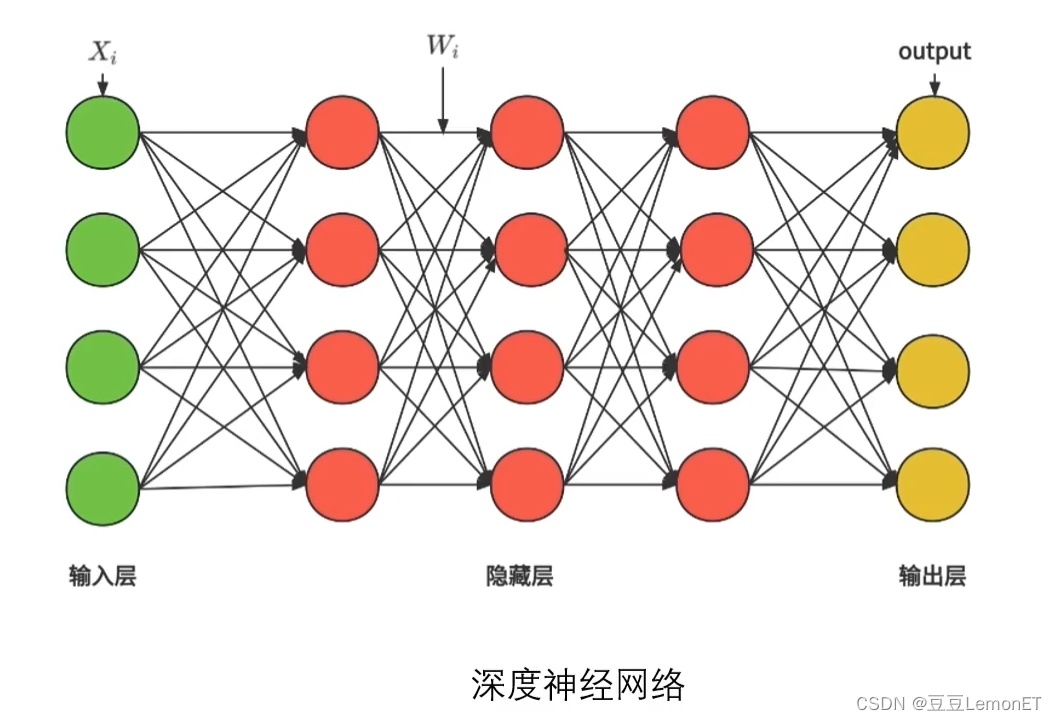
下图为深度神经网络,分为一个输出层,多个隐藏层和一个输出层。
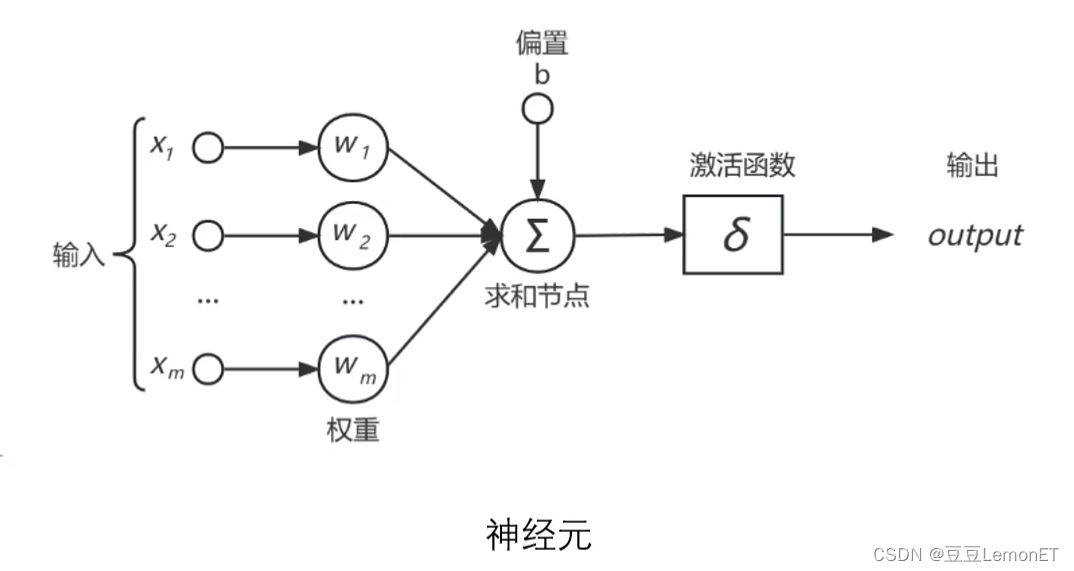
神经元
神经元作为神经网络中最基本的单位,也有其独特的结构,如图所示,其中
- x为输入,每一个连接上都有一个权重w,中间的节点为人工神经元节点;
- δ是一个非线性变换,称为激活函数,目的是为了使人工神经元具有表示非线性关系的能力;
- 参数b称之为偏置;output为人工神经元的输出。
公式如下:
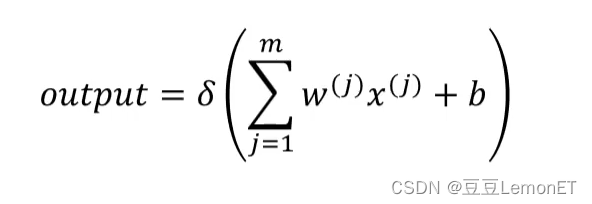
激活函数
激活函数是神经网络中的一种非线性函数,作用于神经元的输入信号,将其转换为神经元的输出。激活函数在神经网络中起到了引入非线性变换的作用,增加了网络的表达能力。
激活函数的主要特点如下:
-
非线性变换:激活函数对输入进行非线性变换,使得神经网络能够学习和表示非线性关系。如果没有激活函数,多个线性层堆叠起来的神经网络仍然只能表示线性关系。
-
可微性:激活函数通常要求在大部分输入范围内是可导的,这是因为梯度下降等优化算法通常依赖于梯度的计算。可导的激活函数使得梯度可以传递并更新网络参数。
-
非饱和性:一些激活函数具有非饱和性,即在输入较大或较小的情况下,能够保持较大的梯度,避免梯度消失问题。这有助于更好地传递误差信号和加速网络的收敛速度。
-
映射范围:激活函数可以将输入信号映射到一定的输出范围内,如Sigmoid函数将输入映射到 (0, 1) 的范围内,而ReLU函数将负值映射为零。这有助于对输出进行限制或规范化。
常见的激活函数包括:
-
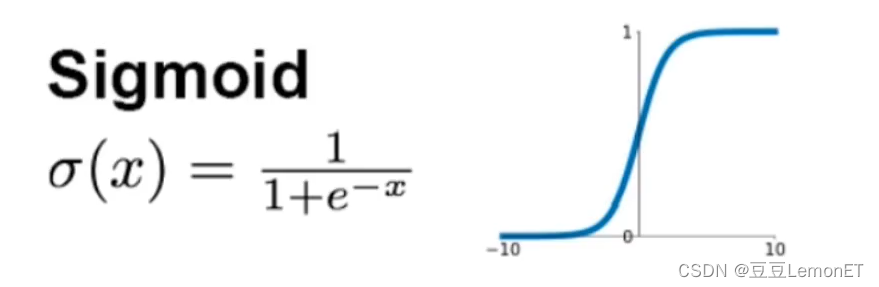
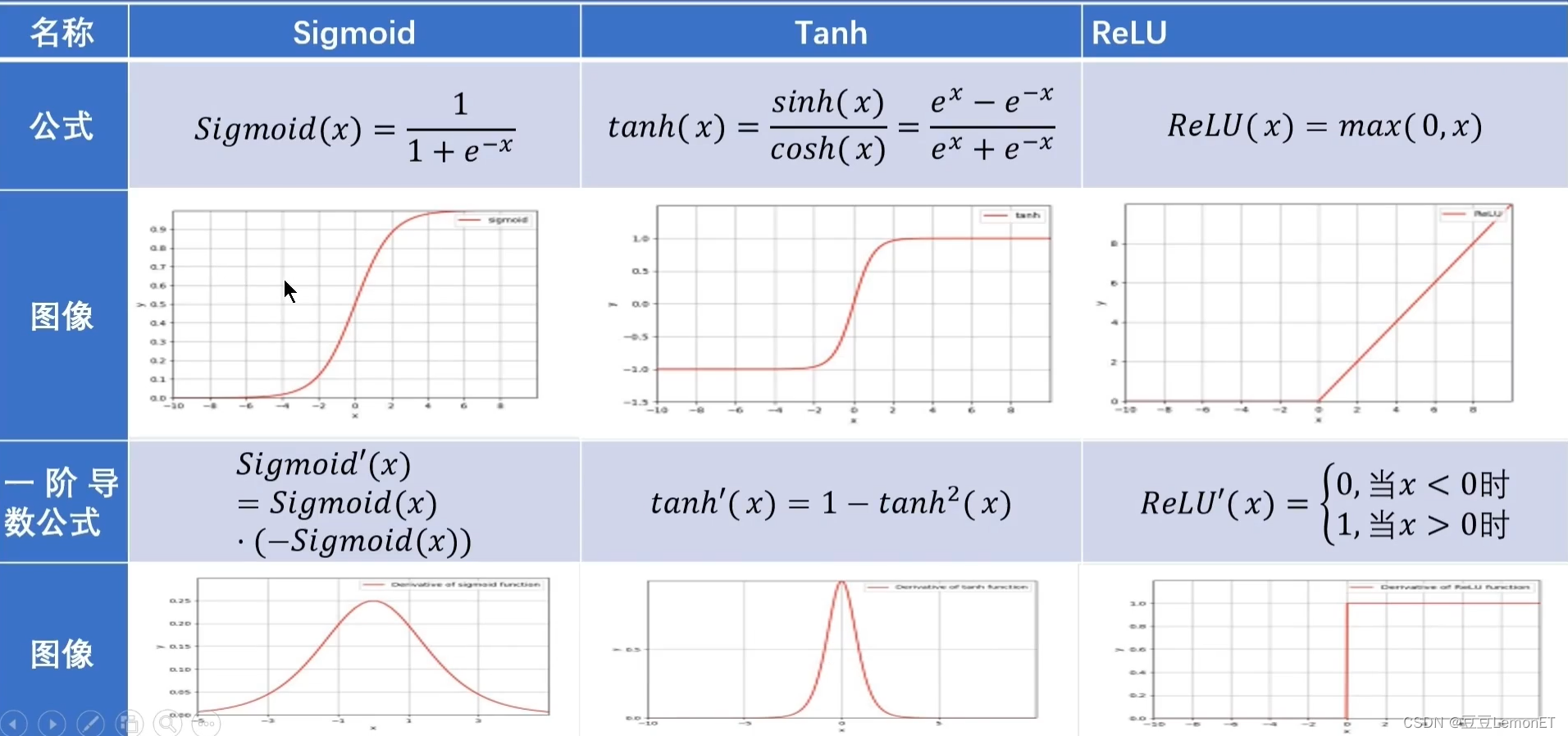
Sigmoid函数:将输入映射到 (0, 1) 的范围内,具有平滑的非线性特性。
-
ReLU函数:在输入大于零时输出等于输入,小于零时输出为零,具有简单和高效的计算方式。
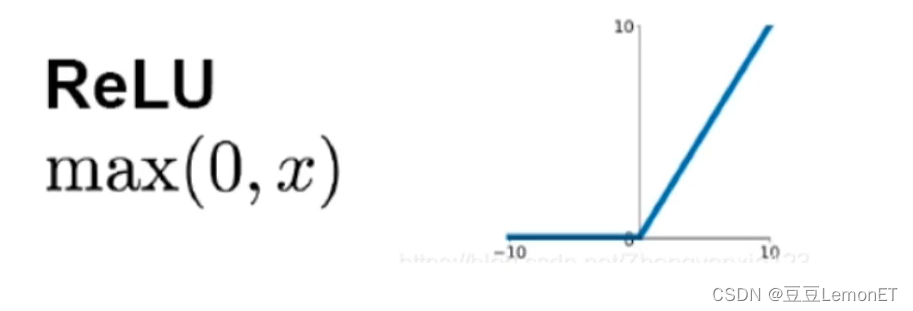
-
Tanh函数:将输入映射到 (-1, 1) 的范围内,形状与Sigmoid函数类似但对称。

-
Leaky ReLU函数:在输入小于零时引入一个小的斜率,避免了ReLU函数的部分问题。
-
Softmax函数:用于多分类问题,在输出层将输入转化为概率分布。
三种激活函数的比较:
损失函数
损失函数是一个数学函数,用于衡量预测值与真实值之间的误差。它可以帮助我们确定模型的预测结果是否准确,并且可以用来评估模型的性能。
损失函数是深度学习中的一个关键因素,它可以帮助我们评估模型的性能并且用于调整模型的参数。选择合适的损失函数能够提高模型的性能,并有助于解决复杂的问题。
常见的损失函数:

内容来自视频:
深度神经网络的结构
这篇关于【神经网络与深度学习】深度神经网络(DNN)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


