本文主要是介绍数学建模-敏感度分析(美赛),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
从多个不确定性因素中逐一找出对投资项目经济效益指标有重要影响的敏感性因素,并分析、测算其对项目经济效益指标的影响程度和敏感性程度,进而判断项目承受风险的能力。若某参数的小幅度变化能导致经济效益指标的较大变化,则称此参数为敏感性因素,反之则称其为非敏感性因素。
当然,敏感性分析表的用途可远不止如此,比如通过它我们还可以做售价-利润率敏感性分析,成本-利润率敏感性分析,售价&地价-利润率敏感性分析,成本&地价-利润率敏感性分析等等。熟练掌握这个技巧以后,我们甚至可以做任何单变量及双变量的敏感性分析。
但是,很多朋友却对敏感性分析表的操作非常陌生,过于依赖测算表格的现有公式链接而无法灵活使用,或者测算公式出现问题以后也不知如何修改。这篇文章我们就一起来系统梳理一下敏感性分析,敏感度分析有以下几种:
1. 理解敏感性分析表
2. 单变量敏感性分析
3. 双变量敏感性分析
4. 多变量敏感性分析
下面以我在建模美赛中的题目实列来阐述:
背景
美国和加拿大的五大湖是世界上最大的淡水湖群。这五个湖泊和相连的水道构成了一个巨大的
流域,其中包含了这两个国家的许多大城市,气候和当地的天气条件各不相同。
湖区的水有多种用途(捕鱼、娱乐、发电、饮用、航运、动物和鱼类栖息地、建筑、灌溉等)。因
此,各种各样的利益相关者都对流入和流出湖泊的水的管理感兴趣。特别是,如果从湖泊排出
或蒸发的水太少,那么可能会发生洪水,沿岸的家庭和企业受到影响;如果排水过多,那么大型
船只就无法通过水路运送补给,支持当地经济。主要问题是调节水位,使所有利益相关者都能
受益。
每个湖泊的水位是由进出湖泊的水量决定的。这些水位是温度、风、潮汐、降水、蒸发、测深
(湖底形状)、河流流量和径流、水库政策、季节周期和长期气候变化等复杂相互作用的结果。在
五大湖系统的水流中有两种主要的控制机制:苏河水闸补偿工程。玛丽(三个水力发电厂,五个航
行船闸和一个在激流顶端的闸门大坝)和康沃尔的摩西-桑德斯大坝,如附录所示。
虽然这两座控制水坝、许多渠道和运河以及流域水库可能是由人类控制的,但降雨、蒸发、侵
蚀、冰塞和其他水流现象的速率是人类无法控制的。地方政府的政策可能会产生与预期不同的
影响,流域的季节和环境变化也可能会产生不同的影响。这些变化反过来又会影响该地区的生
态系统,从而影响湖泊内外动植物的健康以及生活在水盆中的居民。尽管五大湖似乎有一个规
律的年度模式,但水位从正常水平的 2 到 3 英尺的变化会极大地影响一些利益相关者。
这种动态的网络流量问题是“邪恶的”——由于相互依赖、复杂的要求和固有的不确定性,解
决起来异常具有挑战性。对于湖泊的问题,我们有不断变化的动态和利益相关者的利益冲突。
有关附加信息,请参阅问题 D 附录
国际联合委员会(IJC)请求贵公司国际网络控制建模师(icm)提供支持,协助管理和建模直接影响
五大湖水网水位的控制机制(附录中所示的两座水坝-补偿工程和摩西-桑德斯大坝)。你的 ICM
主管已经让你的团队领导开发模型和实施模型的管理计划。你的导师指出,有几个考虑因素可
能有助于实现这一目标,首先是为五大湖建立一个网络模型,并将从苏必利尔湖到大西洋的河
流连接起来。你的导师提到的其他一些可选的考虑因素或问题是:
•考虑到各个利益相关者的愿望(每个利益相关者的成本和收益可能不同),确定五大湖区在一
年中任何时候的最佳水位。
•根据五大湖的流入和流出数据,建立算法以维持五大湖的最佳水位。
•了解您的控制算法对两个控制坝的流出的敏感性。考虑到 2017 年的数据,对于各利益相关者来说,你的新控制方法是否会使当年的实际记录水位令人满意或更好?
•你们的算法对环境条件(例如,降水、冬季积雪、冰塞)的变化有多敏感?
•将您的广泛分析集中在影响安大略湖的利益相关者和因素上,因为最近对该湖的水位管理有更多的关注。
做一些假设,往约束条件中加入此类环境条件变化(降雨量、蒸发量、水流温度、冰塞)对两个控制坝的影响,然后做敏感性分析。以上数据均来自外网记录的往年数据。
敏感性分析的方法
One-at-a-time (OAT)
最简单和最常见的方法之一是每次更改一个因素(OAT),我们这里改变的量也就是单一的环境变化量,以查看这会对输出产生什么影响。OAT包括:
移动一个输入变量,保持其他变量的基线值(nominal value),然后将变量返回到其标称值,然后以相同的方式对每个其他输入进行重复。
之后,敏感性可以通过监测输出的变化来测量,通过偏导数与线性回归方法。在输出中观察到的任何更改都将明确地由单个变量的更改引起。此外,通过每次更改一个变量,可以将所有其他变量固定在它们的基线值,增加了结果的可比较性(与基线情况相比较),并将计算机程序崩溃(同时改变几个因素的情况)的几率降至最低。
我们这里通过偏导数进行敏感度计算
(下面公式我没有全部用到第四介,但是都写上去没有问题)

V-河流流量

不过因为一次只改变一个输入参数,所以不能检测到多个输入耦合的情况。

得到以下环境因素敏感度:
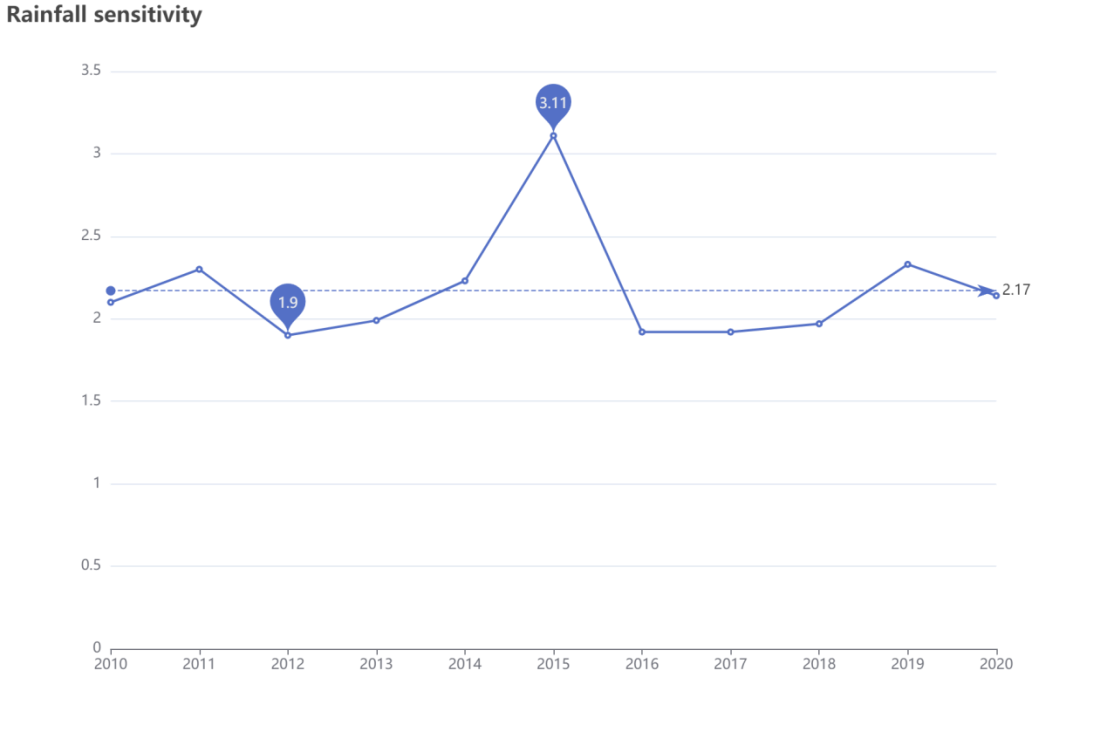
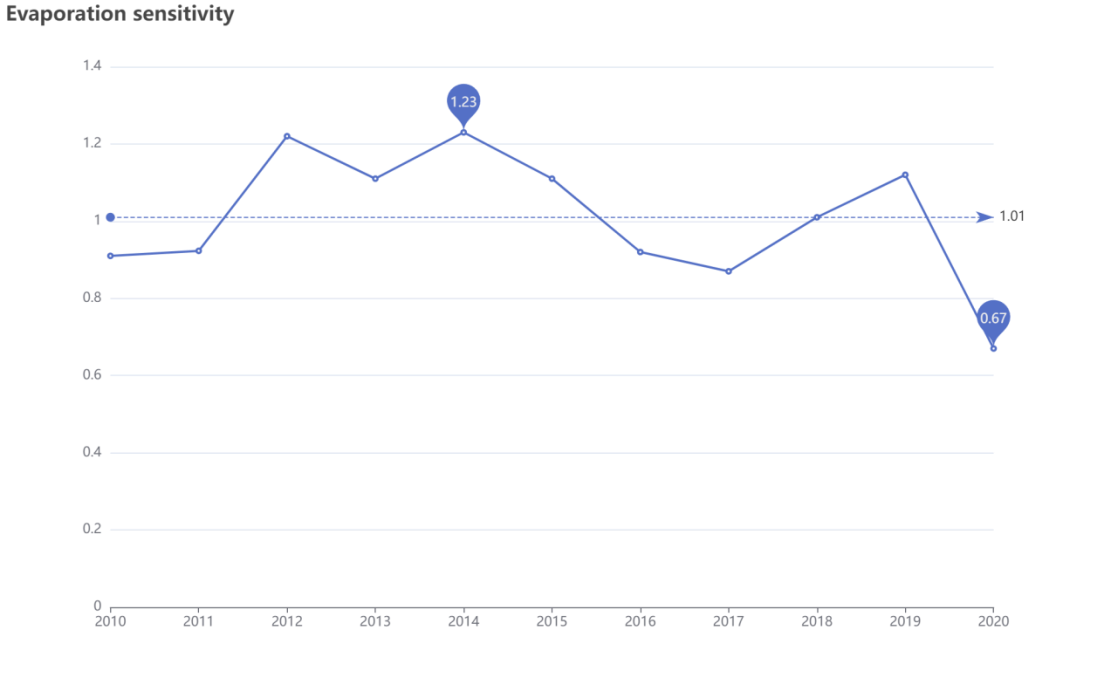
data: [0.91,0.923,1.22,1.11,1.23,1.11,0.92,0.87,1.01,1.12,0.67],
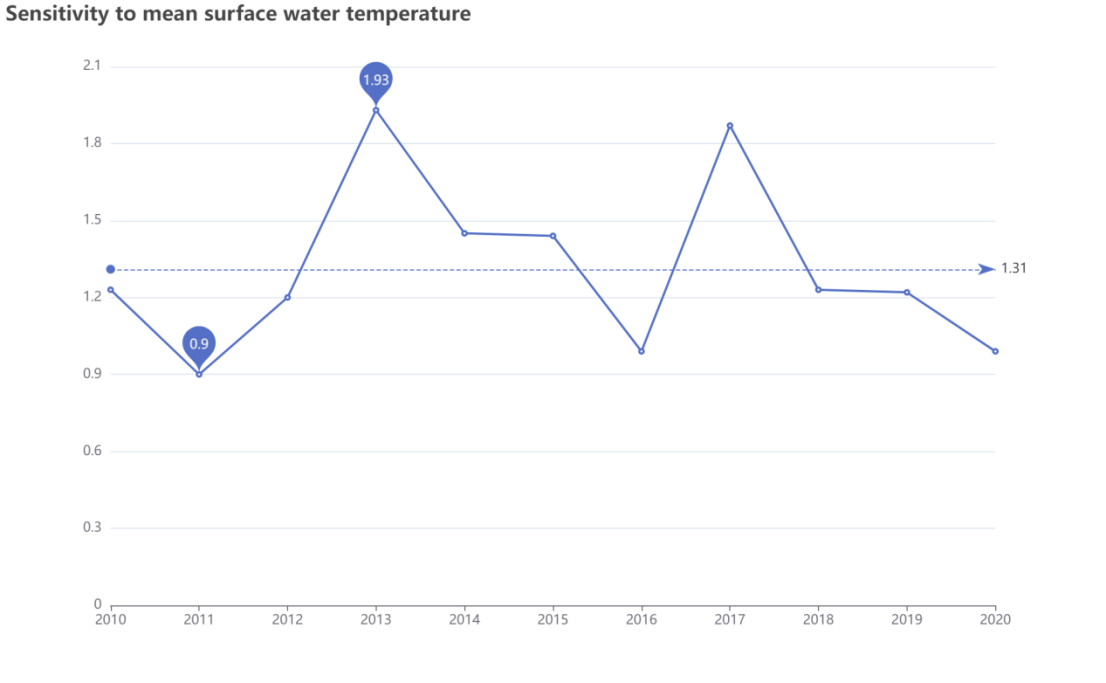
data: [1.23,0.9,1.2,1.93,1.45,1.44,0.99,1.87,1.23,1.22,0.99],
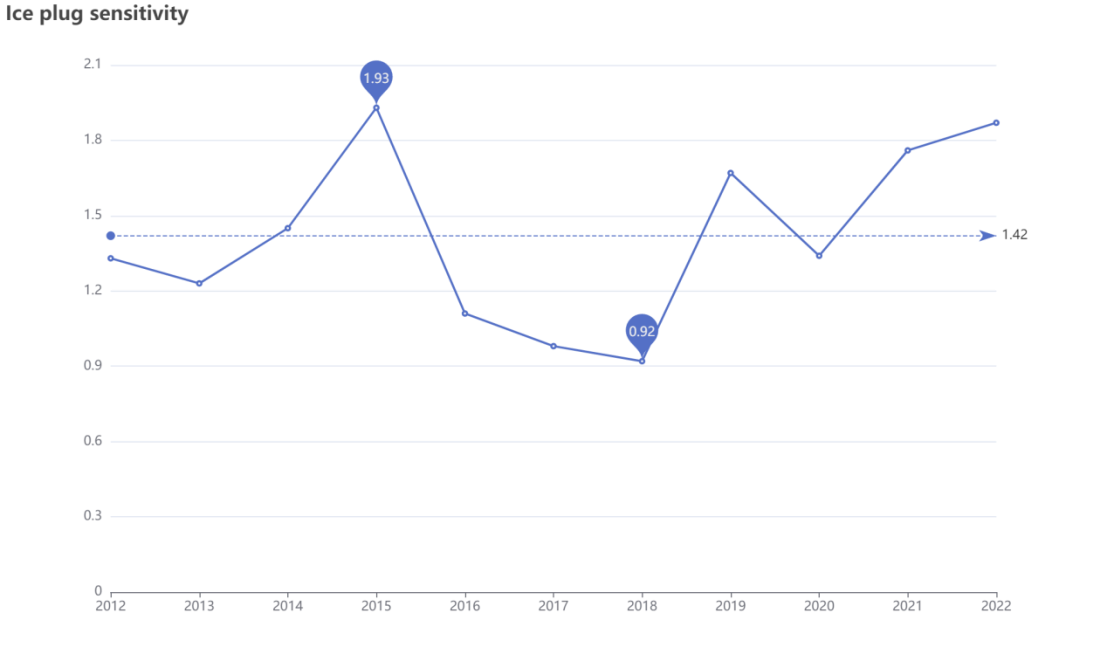
data: [1.33,1.23,1.45,1.93,1.11,0.98,0.92,1.67,1.34,1.76,1.87],
这篇关于数学建模-敏感度分析(美赛)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







