运筹从业者也需要的因果推断入门：基础概念解析和体系化方法理解

本文主要是介绍运筹从业者也需要的因果推断入门：基础概念解析和体系化方法理解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1 引言

已经3月初了，原计划的因果推断学习还没有任何阶段性的成果，不太符合预期。反思了一下，首先是因为春节前后的工作排期异常紧张，没多少精力去学习新东西；其次是因为春节前后放飞了自己，耽搁了持续学习的进程；最后，系列的第一篇文章最难写，希望能够在足够入门的同时对方法体系有大概认知，但又不能太深，所以虽然已经看了很多内容，但始终找不到一个比较合理的行文框架，导致迟迟没有动笔。

本周二的时候，有粉丝找我催更鲁棒优化的内容。想到自己的因果推断入门文章还没完成，紧迫感一下子就上来了。所以，这两天加班加点，先把这个完成了。

正文见下。

2 相关关系 VS 因果关系

因果推断中有一句非常著名的话：相关关系不等于因果关系。在正文的开头，先来梳理一下什么是相关关系和因果关系。

2.1 相关关系

相关关系一般是指两个变量之间的相互关系，通常是一种统计意义上的关系：当两个变量一起增加或减少时，属于正相关关系（a图）；当一个变量随着另一个变量的增加而较少时，属于负相关关系（b图）；当一个变量对另一个变量的增加或减少无动于衷时，认为是没有相关关系（c图）。

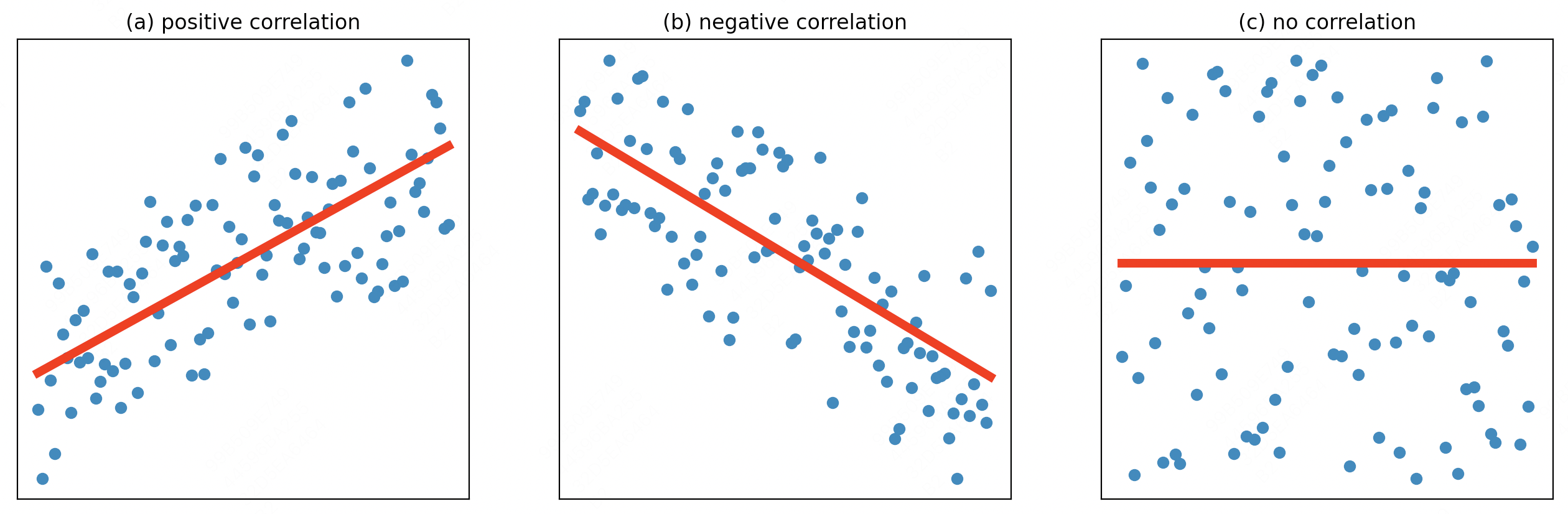
统计学中，一般使用相关系数来量化相关关系。常见的相关系数有：Pearson相关系数、Spearman等级相关系数和Kendall等级相关系数。工业界最常用的是Pearson相关系数，下面我们来着重理解一下这个相关系数。

假设有两个变量$X$和$Y$，他们之间的Pearson相关系数的数学表达式为
$${\rho }_{X,Y}=\frac{Cov(X,Y)}{{\sigma }_X{\sigma }_Y}=\frac{E[(X-{\mu }_X)(Y-{\mu }_Y)]}{{\sigma }_X{\sigma }_Y}$$
式中，$Cov$表示协方差，$\mu$表示均值，$\sigma$表示方差。上面这个公式不太好理解，我们用分量的形式重写一下
$${\rho }_{X,Y}=\frac{{\sum }_{i=1}^N(x_i-{\mu }_x)(y_i-{\mu }_Y)}{\sqrt{{\sum }_{i=1}^N(x_i-{\mu }_X{)}^2}\cdot \sqrt{{\sum }_{i=1}^N(y_i-{\mu }_Y{)}^2}}$$
定义：$x_i^{\prime }=x_i-{\mu }_x,y_i^{\prime }=y_i-{\mu }_y$，上式变为
$${\rho }_{X,Y}=\frac{{\sum }_{i=1}^N{x}_i^{\prime }{y}_i^{\prime }}{\sqrt{{\sum }_{i=1}^N{x}_i^{\prime 2}}\cdot \sqrt{{\sum }_{i=1}^N{y}_i^{\prime 2}}}=\frac{X^{\prime }{Y}^{\prime }}{|X^{\prime }||Y^{\prime }|}=\cos (X^{\prime },Y^{\prime })$$
所以，Pearson相关系数可以理解为：将原向量$X$和$Y$做中心化之后的新向量$X^{\prime }$和$Y^{\prime }$间夹角的余弦值。有了这层理解，便可知，Pearson相关系数值的范围是$[-1,1]$。

下图展示了不同Pearson相关系数值时的变量分布情况。

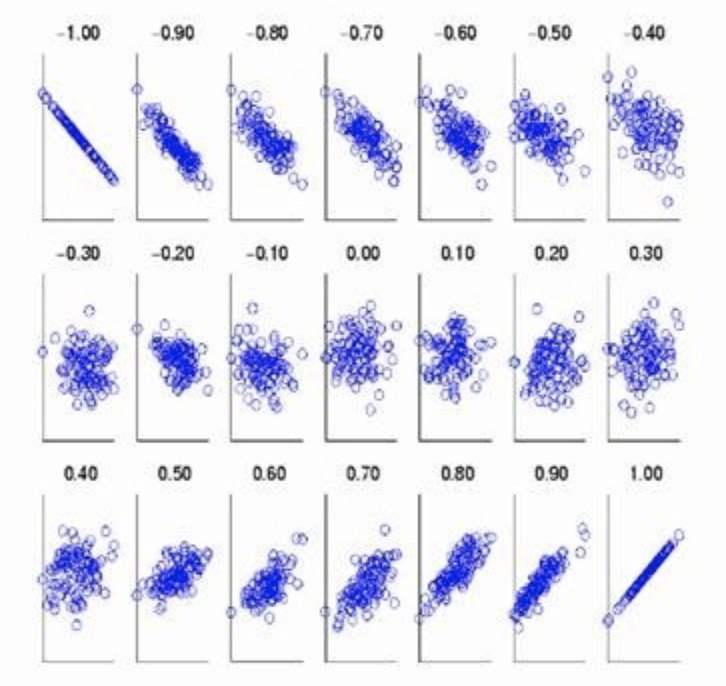
2.2 因果关系

与相关关系相比，因果关系区分了原因变量和结果变量。借助自然科学研究的思路来定义因果关系，即假设存在两个变量$X$和$Y$，在控制能影响$Y$的一切其他变量保持不变的同时，改变$X$的状态，观察$Y$是否随之发生改变。如果$Y$发生了改变，那么则称$X$是$Y$的原因，$Y$是$X$的结果，$X$与$Y$之间具有因果关系。

工业界一般习惯使用uplift去表征$X$和$Y$之间量化的因果效应，从因果关系的定义上可以推导出

$$\text{uplift}=E(Y|X=1)-E(Y|X=0)$$

显然，该值越大，他们之间的因果关系越强。

直观上来看，$X$和$Y$的相关关系描述的是“$Y$随$X$的变化而变化的趋势”；$X$和$Y$的因果关系研究的是“有X时的Y”和“没有X时的Y”之间的差值。

为了更直观地展示他们之间的差异，我们举个广告中的实例，如下表所示。此处，$X$对应的是广告，$Y$对应的是商品转化率。如果研究广告和商品转化率之间的相关关系，一般指的是看过广告后的的商品转化率，此时第2批用户的相关系数值更大（2%）；但如果研究广告和商品转化率之间的因果关系，一般指的是因为广告而导致的商品转化率，此时第1批用户的uplift值更高（0.9%）。

用户批次	有广告时的平均商品转化率	无广告时的平均商品转化率	uplift
1	1%	0.1%	0.9%
2	2%	1.5%	0.5%

事实上，如果仅能选取一批人进行广告投放，那么最佳的策略显然是将广告投放给因果关系更强的第一批用户。而这也是研究因果关系的价值之一：它可以为我们的最优决策提供理论基础。

2.3 相关关系不等于因果关系

上一节的广告实例已经直观地告诉了我们，相关关系和因果关系研究的内容是有差异的。即便如此，我们还是希望能使用相关关系代表因果关系。这是因为，相关关系更直观，而且作为一个统计指标，可以使用很多成熟的数学方法对其进行量化。

为此，我们有必要知道，哪些情况会导致相关关系和因果关系不对等。最容易想到的一种情况是：样本有选择性偏差。如果研究中使用的样本并不能充分代表整个总体，那么研究的结论就可能偏离真实情况。特别地，如果将对撞子作为划分样本的变量，就可能导致得到相关关系和真正的因果关系不一致。此处，对撞子指的是原因变量和结果变量共同的结果。

举个例子，我们想研究饮食健康和作息规律程度之间的因果关系。如果选择健康人群，两个变量相对比较均衡，可能会没有显著的因果关系；但如果选择患病人群，那么可能会发现，如果饮食健康，那么作息就不规律；如果作息规律，那么饮食就不健康，即两个变量间存在负相关关系。这种情况下，选择不同的人群，便得到了不同的相关关系，但真正的因果关系只有一个，由此可能导致了相关关系和因果关系的不一致。

另一种导致相关关系和因果关系不对等的情况稍微复杂：夹杂了混杂因子。混杂因子指的是既影响原因变量也影响结果变量的变量。举个例子，我们想研究作息规律程度与肠胃疾病患病率之间的相关关系和因果关系。样本的散点图如下图黑色圆点所示。

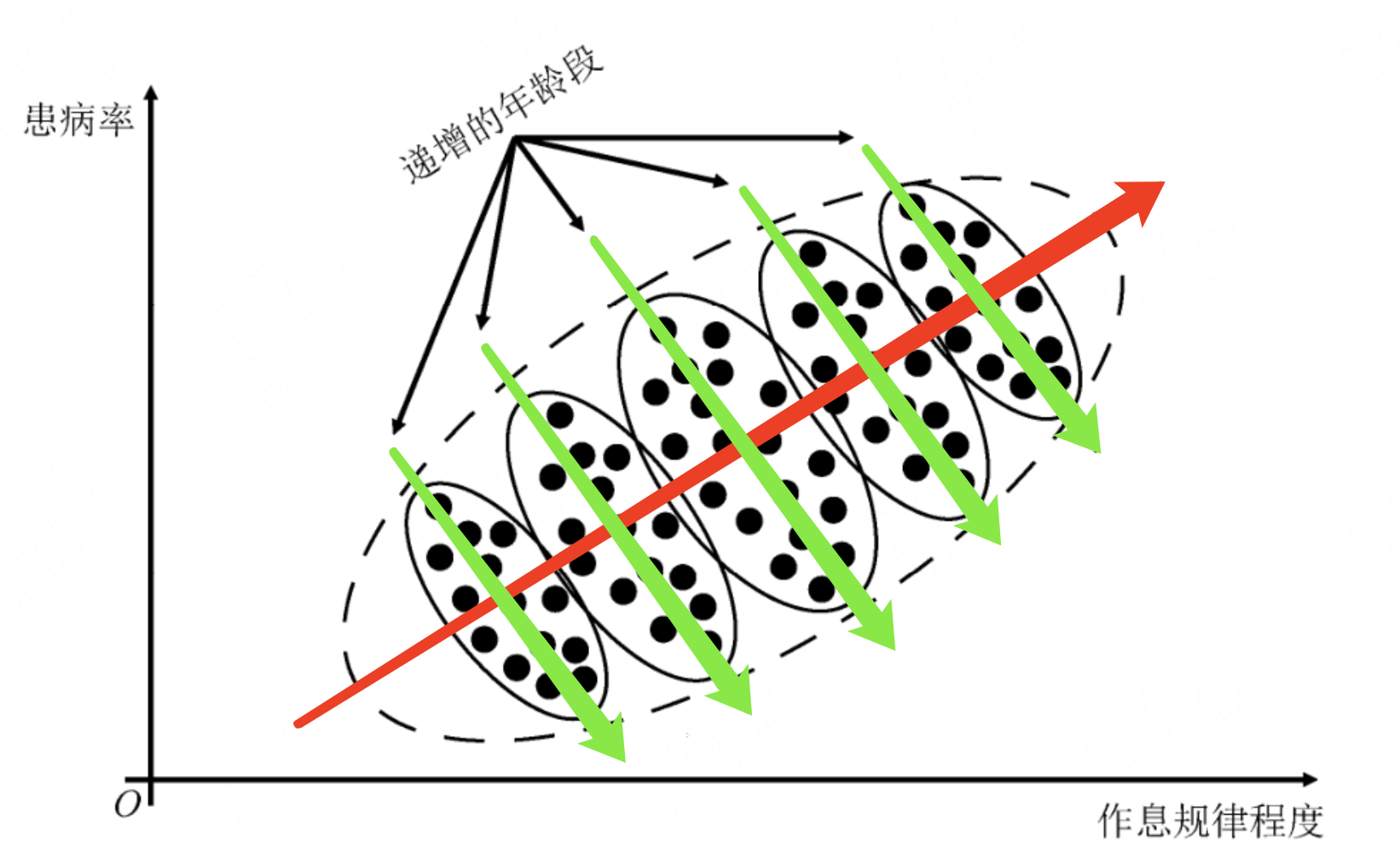
从整体的相关关系来看，患病率和作息规律程度是呈明显的正相关关系（红色箭头），但是如果我们直接给出“作息规律程度的提升会导致患病率提升”的因果关系结论，显然是和我们的常识相悖的。这就是因果推断中辛普森悖论的一个实例。

出现该悖论的原因是存在混杂因子：年龄。一方面，年龄越大，人们越重视作息，规律性越强；另一方面，年龄越大，身体机能越差，患病率也会提升。

这种情况下，如果想探查出真正的因果关系，就需要去除混杂因子：将样本限定在同一个年龄段内。此时我们发现，无论在哪个年龄段，作息越规律，患病率都会越低（绿色箭头），因此可以得到结论：规律的作息有助于降低患病率。

3 因果推断方法

3.1 方法体系

既然不能直接用相关关系替代因果关系，那么就需要单独的方法去做因果推断。

我翻阅了一些书籍，感觉有本书针对因果推断的方法论体系的描述很容易让人理解：《因果推断：原理解析与应用实践》。

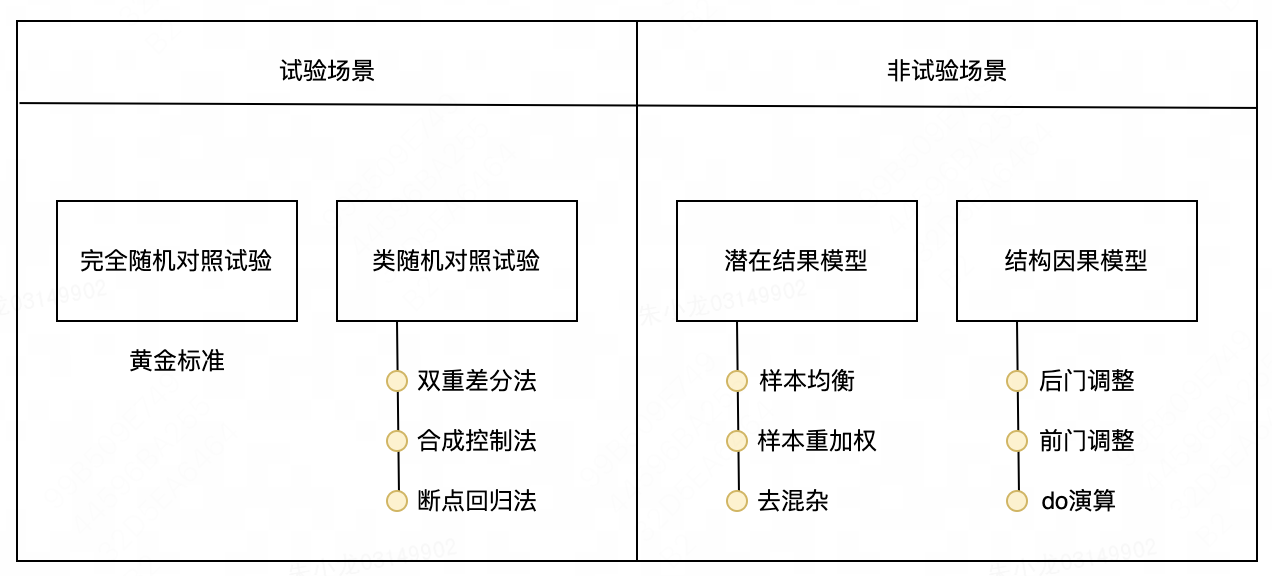
本节将参考该书中使用的因果推断方法体系，来描述因果推断的各类方法，并增加一些实例来加深对这些方法的认知和理解，具体如下图所示。

（1）试验场景：完全随机对照试验中，没有混杂因子也没有样本选择偏差，此时设置实验组的原因变量$X=1$，对照组$X=0$，再计算实验组和对照组的结果变量之差，就可以得到uplift值，它是量化因果关系的黄金标准；类随机对照试验中，会将试验数据通过差分、组合等方式将原始数据还原成完全随机对照试验的情况。

（2）非实验场景：潜在结果模型中，不需要再做试验，而是根据已经观测到的数据通过一些计算直接得到uplift，是一种可以得到因果关系结论的理想模式；结构因果模型中，使用有向图来建模变量间的因果关系。

3.2 方法理解

完全随机对照试验，很容易理解，不需要赘述；类随机对照试验中的双重差分法，我此前已经写过两篇文章，双重差分法（DID）：算法策略效果评估的利器和双重差分法：标准化流程和stata代码实现，其他方法后面学习的时候再详细介绍。

潜在因果模型可以用下表来理解。针对特定用户，我们实际上只能观察到其中一条数据，但要计算uplift值，就必须同时知道两条数据。在潜在因果模型中，会使用机器学习的方法，把未观测到的另一条数据给预测出来。至于如何让预测的结果可靠，后面学习的时候再详述（关于机器学习的原理，可以参考：运筹视角下，体系化学习机器学习算法原理的实践和总结）。

用户	有广告时的商品转化率	无广告时的商品转化率	uplift
1	1%	？	1-？
2	？	1.5%	？-1.5%

关于结构因果模型的理解，我们也举个实例。下表是一个关于新药物是否可以降低心脏病发作的实验数据，其中分子是心脏病不发作的数量，分母是对应组别下的总人数。限定性别时，我们发现服药组不发作的概率均高于对照组；不管性别直接看总数时，我们却发现服药组不发作的概率低于对照组。事实上，这还是个辛普森悖论的实例。

	服药组	未服药组
男性	81/87=0.93	234/270=0.87
女性	192/263=0.73	55/80=0.69
总数	273/350=0.78	289/350=0.83

为了确定新药物是否可以降低心脏病发作，结构因果模型的推演过程包含三步：关联、干预和反事实推断。

第一步，关联：从原表可以看出，心脏病发作的概率同时受性别和是否服用药物影响，是否服用药物也受性别影响，所以因果图如左下图所示（干预前）。此处，节点通过有向边连接到一个或多个与其有因果关系的其他节点，有向边则反映了因果关系的方向。

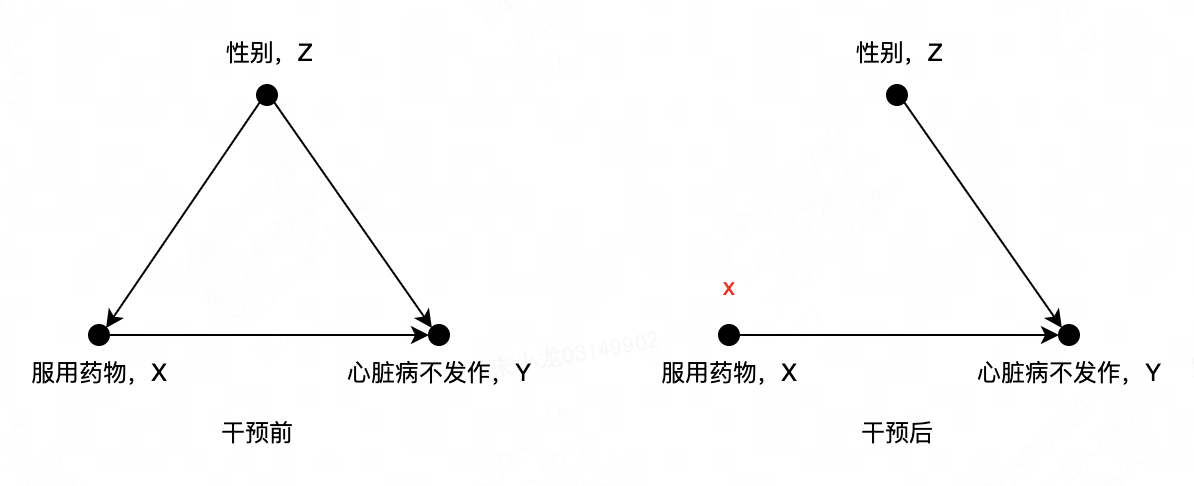
第二步，干预：我们让所有人都服用药物$X=1$，以及所有人都不服用药物$X=0$。此时，性别已经不再影响是否服用药物，所以因果图变成右上图（干预后）。

第三步，反事实推断：分别计算两种干预情况下，心脏病不发作的概率。
$$P(Y=1|X=1)=P(Y=1|X=1,Z=1)P(Z=1)+P(Y=1|X=1,Z=0)P(Z=0)=0.93\times \frac{87+270}{87+270+263+80}+0.73\times \frac{263+80}{87+270+263+80}=0.83$$
$$P(Y=1|X=0)=P(Y=1|X=0,Z=1)P(Z=1)+P(Y=1|X=0,Z=0)P(Z=0)=0.87\times \frac{87+270}{87+270+263+80}+0.69\times \frac{263+80}{87+270+263+80}=0.78$$
上述两式是基于全概率公式推导出来的，它能用在此处的原因是：在干预后，性别和是否服用药物之间是相互独立的。细节原理不清楚没关系，后面详细学习的时候应该还会再说，此处有个大致印象就行。

由于$P(Y=1|X=1)$大于$P(Y=1|X=0)$，所以可以得到结论：新药物有利于提升心脏病不发作的概率。

4 运筹从业者也需要因果推断

关于因果推断的入门内容，到这里其实已经结束了。

但，作为运筹优化方向的算法工程师，为什么要学习因果推断，还是没有充分阐述。

接下来我们将通过一个行业实践的案例：DiDi Food中的智能补贴实战漫谈，来讲解因果推断是如何与运筹优化相结合来解决业务问题的。

4.1 问题描述

这个案例的基本背景是：业务方DiDi Food是一个外卖平台，它们希望通过对用户做差异化定价，提升某些指标。

针对任意一件商品，用户看到的最终价格$P$通过下述公式计算得到
$$P=P_i+P_d-S_c$$

其中，$P_i$为菜品标价（商品侧），$P_d$为配送费（骑手侧），$S_c$为C端补贴（用户侧）。

作为一个平台，DiDi Food很难拥有菜品价格的定价权，在设置配送费时也会尽量不使用用户维度的特征，以避免出现大数据杀熟的现象，所以最终确定以$S_c$为主要抓手，通过给不同用户发放不同类型的补贴，动态调整$P$值，目标是最大化如下指标
$$ROI=\frac{指标Y_{干预}-指标Y_{不干预}}{补{贴}_{干预}-补{贴}_{不干预}}$$
$ROI$可以理解为单位补贴成本带来的指标$Y$的增量收益，所以该值越大越好。

4.2 算法方案

针对以上问题，算法方案包括两个步骤：（1）分析用户对补贴的敏感性并进行量化；（2）基于量化的敏感度值和业务约束，做补贴的最佳分配。

先看第一步。一般来说，可以定性的把用户分为如下四种：(1)自然转化：有没有补贴都会下单；(2)补贴敏感：没有补贴就不下单，有补贴才会下单；(3)反作用：没有补贴时会下单，有补贴反而不会下单；(4)无动于衷：有没有补贴都不会下单。

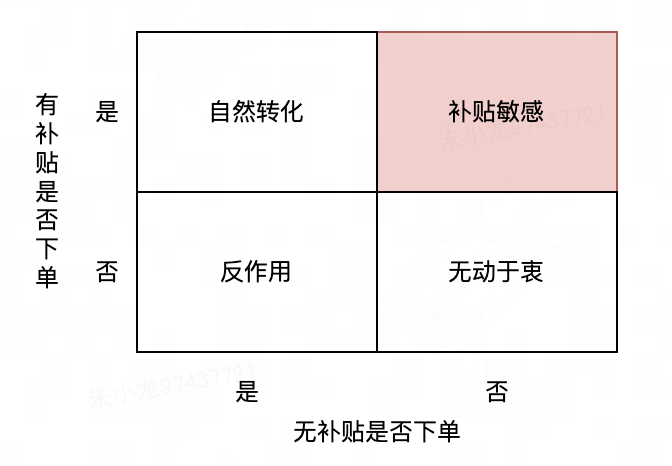
基于最朴素的认知也很容易得到如下结论：如果要最大化$ROI$，应该把补贴发放给补贴敏感的用户，其他用户就不用补贴了。

不过，即使都是补贴敏感的用户，他们对补贴敏感的程度也是有差异的。为了对这些人群也做区分，我们就需要量化用户对补贴的敏感度uplift。下表给出了一些实例。

用户	无补贴下单概率	有补贴下单概率	uplift	备注
1	0	0	0	无动于衷
2	0.5	0.55	0.05	补贴敏感度次之
3	0.5	0.4	-0.1	反作用
4	0.2	0.2	0	自然转化
5	0	0.5	0.5	补贴最敏感

然后再看第二步。假设目前有10个用户，有3种补贴券，分别都有1张。那么针对每种补贴券，每个用户都会有一个对应的uplift。此时的问题可以转化为：如何为每个用户分配一种补贴券，从而最大化总的uplift值。

这是个标准的整数规划问题，可以建模如下
max ⁡ ∑ i = 1 10 ∑ j = 1 3 x i j ⋅ u i j s.t ∑ i = 1 10 x i j = 1 , j = 1 , 2 , 3 ∑ i = 1 10 ∑ j = 1 3 x i j ⋅ w j ≤ W x i j ∈ { 0 , 1 } \max \quad \sum_{i=1}^{10}\sum_{j=1}^3 x_{ij}·u_{ij} \\ \text{s.t} \quad \sum_{i=1}^{10}x_{ij}=1, j=1,2,3 \\ \sum_{i=1}^{10}\sum_{j=1}^3 x_{ij}·w_j ≤W \\ x_{ij}\in \{0,1\} maxi=1∑10​j=1∑3​xij​⋅uij​s.ti=1∑10​xij​=1,j=1,2,3i=1∑10​j=1∑3​xij​⋅wj​≤Wxij​∈{0,1}
此处，$x_{ij}$表示是否对用户$i$发放第$j$种补贴券，值为1时表示发放，值为0时表示不发放；$u_{ij}$表示用户$i$对第$j$种补贴券的uplift；$w_j$表示第$j$种券的补贴金额；$W$表示允许的最大补贴额。

4.3 算法验证

假设线上正在运行的是基于人工经验设计的补贴方案B，我们也开发完成了上述的算法方案A。目前需要验证A是否显著优于B，如果是，后续便可以替换B为A。

验证的方法是做线上实验：选取3组几乎相同的人群，分别定义为：实验组、对照组和空白组，它们使用的补贴方案分别为：A、B和无补贴。

经过一段时间的实验后，回收三组对应的指标$Y$及其对应的补贴金额，便可以通过计算和对比实验组的$ROI$和对照组的$ROI$值，得到A是否显著优于B的结论。

从前文的描述可以看出，算法方案中的第二个步骤属于运筹优化内容，而算法方案中的第一个步骤和算法验证模块均属于因果推断的内容。所以，在实际工作中如果想要解决好这类业务问题，很难避开因果推断。

5 总结

本文稍微有些长，最后再总结一下：

（1）相关关系不等于因果关系，出现不对等的原因可能是：样本有选择性偏差、有混杂因子；相关关系使用Pearson相关系数去量化，因果关系使用uplift去量化。

（2）因果推断的方法分为两大类：试验场景和非试验场景，试验场景中包含完全随机对照试验和类随机对照试验；非试验场景分为潜在因果模型和结构因果模型。

（3）运筹从业者也需要因果推断。

6 相关阅读

赵永贺等编著.因果推断：原理解析与应用实践[M], 北京: 电子工业出版社, 2023：https://weread.qq.com/web/bookDetail/813326f0813ab873fg015d1a

因果推断（一）：因果推断两大框架及因果效应：https://zhuanlan.zhihu.com/p/652174282

DiDi Food中的智能补贴实战漫谈：https://mp.weixin.qq.com/s/WU1iILMFdH3RZAbJKFU4WA

皮尔逊相关系数的几何理解：https://oychao.github.io/2016/05/18/statistics/03_pearsons_r/

因果推理初探（4）——干预：https://zhuanlan.zhihu.com/p/111340526

动手学因果推断】（二）：潜在因果框架：https://blog.csdn.net/weixin_45052363/article/details/129842753

这篇关于运筹从业者也需要的因果推断入门：基础概念解析和体系化方法理解的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---