红黑树的删除真的很难吗？其实是你没找到好的解题思路，不信你点击进来看看...

红黑树删除节点

  红黑树的节点的删除其实也分为两步：

1. 先删除节点(这步和普通的二叉树删除是一样的)

2. 然后再调整

1.删除节点

  要删除这个节点先需要找到这个节点，找到节点就是普通的二分查找，具体代码如下

    private RBNode getNode(K key){RBNode node = this.root;while (node != null ){int cmp = key.compareTo((K) node.key);if(cmp < 0){// 在左子树node = node.left;}else if(cmp >0){// 右子树node = node.right;}else{return node;}}return null;}

  在整理红黑树节点的删除操作时我们需要先理解清楚红黑树删除和2-3-4树删除的等价关系，这样理解起来才会比较容易
  核心理论：红黑树删除操作的本质其实就是删除2-3-4树的叶子节点

情况2：删除的是非情况1的节点，根据我们前面介绍的删除的规则，会找到对应的前驱和后继节点，那么最终删除的还是叶子节点

首先删除节点的代码为：

/*** 删除节点* @param key* @return*/public V remove(K key){// 先找到这个节点RBNode node = getNode(key);if(node == null){return null;}// 把值存起来 删除后 返回V oldValue = (V) node.value;deleteNode(node);return oldValue;}/*** 删除节点*   3种情况* 1.删除叶子节点，直接删除* 2.删除的节点有一个子节点，那么用子节点来替代* 3.如果删除的节点右两个子节点，此时需要找到前驱节点或者后继节点来替代*    可以转换为 1、2的情况* @param node*/private void deleteNode(RBNode node){// 3.node节点有两个子节点if(node.left !=null && node.right != null){// 找到要删除节点的后继节点RBNode successor = successor(node);// 然后用后继节点的信息覆盖掉 要删除节点的信息node.key = successor.key;node.value = successor.value;// 然后我们要删除的节点就变为了 后继节点node = successor;}// 2.删除有一个子节点的情况RBNode replacement = node.left != null ? node.left : node.right;if(replacement != null){// 替代者的父指针指向原来 node 的父节点replacement.parent = node.parent;if(node.parent == null){// 说明 node 是root节点root = replacement;}else if(node == node.parent.left){// 双向绑定node.parent.left = replacement;}else{node.parent.right = replacement;}// 将node的左右孩子指针和父指针都指向null node等待GCnode.left = node.right = node.parent = null;// 替换完成后需要调整平衡if(node.color == BLACK){// fixAfterRemove(replacement)}}else if(node.parent == null){// 说明要删除的是root节点root = null;}else{// 1. node节点是叶子节点 replacement为null// 先调整if(node.color == BLACK){// fixAfterRemove(node)}// 再删除if(node.parent != null){if(node == node.parent.left){node.parent.left = null;}else{node.parent.right = null;}node = null;}}}

然后就是需要调整红黑树的平衡了。

2.删除后的平衡调整

删除节点的调整操作：

1.情况一：自己能搞定的，对应叶子节点是3节点和4节点

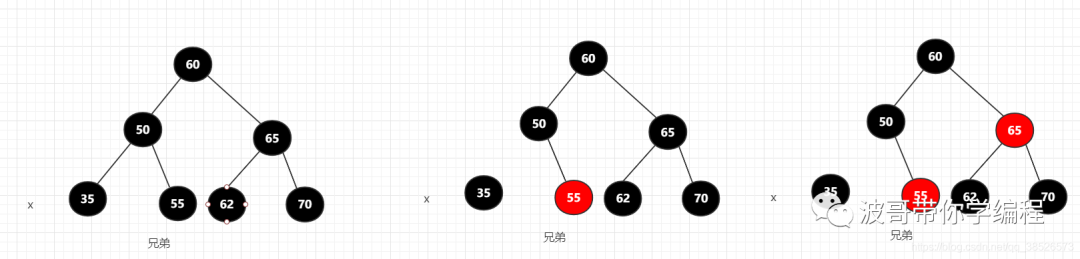
2.情况二：自己搞不定，需要兄弟借，但是兄弟不借，找父亲借，父亲下来，然后兄弟找一个人去代替父亲当家

这种情况就是兄弟节点是3节点或者4节点

找兄弟节点

执行如下调整先,先变色，然后左旋

找兄弟节点借

3.情况三：跟兄弟借，兄弟也没有（情同手足，同时自损）

兄弟节点是2节点，同时当前节点的父节点是红色节点的情况

兄弟节点是2节点，同时当前节点的父节点是黑色节点

分析清楚了删除的3中情况，我们就可以撸处删除的调整的代码了

    /*** 2-3-4树删除操作：* 1.情况一：自己能搞定的，对应叶子节点是3节点和4节点* 2.情况二：自己搞不定，需要兄弟借，但是兄弟不借，找父亲借，父亲下来，然后兄弟找一个人去代替父亲当家* 3.情况三：跟兄弟借，兄弟也没有* @param x*/private void fixAfterRemove(RBNode x){// 情况2、3while(x != root && colorOf(x) == BLACK){// 这种情况才需要调整// x 是左孩子的情况if(x == leftOf(parentOf(x))){// 找兄弟节点RBNode rNode = rightOf(parentOf(x));// 判断此时的兄弟节点是否是真正的兄弟节点 兄弟是红色的情况要调整if(colorOf(rNode) == RED){ // 2-3-4树的 3节点 交换颜色，然后左旋一次就可以了setColor(rNode,BLACK);setColor(parentOf(x),RED);leftRotate(parentOf(x)); // 左旋一次rNode = rightOf(parentOf(x)); // 找到真正的兄弟节点}// 情况3 找兄弟借 没得借if(colorOf(leftOf(rNode)) == BLACK && colorOf(rightOf(rNode)) == BLACK){// 情况复杂setColor(rNode,RED);x=parentOf(x); // 向上递归}else{// 情况2 找兄弟借 有借// 兄弟节点是 3节点或者4节点if(colorOf(rightOf(rNode)) == BLACK){// 右孩子为空，则左孩子肯定不为空// 兄弟节点 先要左一次右旋setColor(rNode,RED);setColor(leftOf(rNode),BLACK);rightRotate(rNode);// 重新调整叔叔节点的位置rNode = rightOf(parentOf(x));}// 变色  兄弟节点是 3节点还是4节点 都旋转一次setColor(rNode, colorOf(parentOf(x)));setColor(parentOf(x),BLACK);setColor(rightOf(rNode),BLACK);// 左旋leftRotate(parentOf(x));x = root; // 结束循环  递归 针对的是 情况3}}else{// 找兄弟节点RBNode rNode = leftOf(parentOf(x));// 判断此时的兄弟节点是否是真正的兄弟节点 兄弟是红色的情况要调整if(colorOf(rNode) == RED){ // 2-3-4树的 3节点 交换颜色，然后左旋一次就可以了setColor(rNode,BLACK);setColor(parentOf(x),RED);rightRotate(parentOf(x)); // 左旋一次rNode = leftOf(parentOf(x)); // 找到真正的兄弟节点}// 情况3 找兄弟借 没得借if(colorOf(rightOf(rNode)) == BLACK && colorOf(leftOf(rNode)) == BLACK){// 情况复杂setColor(rNode,RED);x=parentOf(x); // 向上递归}else{// 情况2 找兄弟借 有借// 兄弟节点是 3节点或者4节点if(colorOf(leftOf(rNode)) == BLACK){// 右孩子为空，则左孩子肯定不为空// 兄弟节点 先要左一次右旋setColor(rNode,RED);setColor(leftOf(rNode),BLACK);leftRotate(rNode);// 重新调整叔叔节点的位置rNode = leftOf(parentOf(x));}// 变色  兄弟节点是 3节点还是4节点 都旋转一次setColor(rNode, colorOf(parentOf(x)));setColor(parentOf(x),BLACK);setColor(leftOf(rNode),BLACK);// 左旋rightRotate(parentOf(x));x = root; // 结束循环  递归 针对的是 情况3}}}// 情况1：替代节点是红色，直接染黑  在情况3的情况下  补偿删除的黑色节点，这样红黑树依然保存平衡setColor(x,BLACK);}

~好了，到这儿，相信大家应该对红黑树的各种操作都比较清楚了，如果对你有帮助，欢迎点赞关注加收藏哦！！！V_V