最短路径问题(dj和floyd算法)

本文主要是介绍最短路径问题(dj和floyd算法)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 首先是dj算法，dj算法的思想是从开始结点开始，每次找到距离开始结点距离最近的结点newP，加入到集合K中，表示已经访问过，然后遍历newP的直接相邻的结点，如果从newP结点开始到直接相邻的结点 i 的距离Dis[newP]+c < Dis[i]，那么就更新Dis[i]，扫描完成所有newP的邻接结点，然后遍历所有的结点，找到未访问过的并且Dis[i]最小的结点 j ，设为新的 newP ，重复上述步骤，直到所有的结点都完成了访问。

设置一个Dis[i]矩阵，表示从1到该结点的距离，Dis[1] = 0, 开始时其它结点的Dis[1] = -1.从1开始进行循环。

如果要打印最短路径，可以设置一个vector<int> pre[N], 每个结点 i ，将在更新Dis[i]时，更新 pre[i].push_back(newP)， 通过newP到达 i 是当前从1到达i 的最短路径的上一个结点，这样从后向前打印即可。

看下面的这个例子：

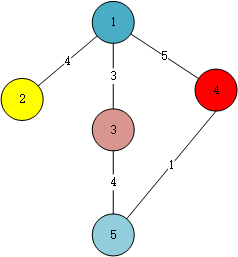
从1出发，找到最短的邻接点 3，访问；从 3 开始遍历 3 的邻接点， 更新5的Dis[5] = 7, 从未访问的结点2，4,5中找到最近的结点2，访问，然后是4访问，遍历4的邻接点，Dis[5]更新为6，最后访问5；完成；

问题是：给出N个地点，M个直接路径，直接路径包括两端地点和它们直接长度，找出1到N号地点的最短路径：

代码为：

#include<cstdio>
#include<vector>
#include<math.h>
#include<algorithm>
using namespace std;
#define N 101
struct E{int next;int c;
};
vector<E> edge[N];//edge[i]中的与元素是一个个的E类型，包含了直接相连号和边权
bool mark[N];//表示该结点是否已经加入到最短路径已知集合中
int Dis[N];//从开始结点到任意结点的最短路径长度度int main()
{int n,m;//n个地点，m个直接相连路径，求从1到n的最短路径while(scanf("%d%d", &n, &m) != EOF){if(n == 0 && m == 0)break;for(int i = 1; i <= n; i++)edge[i].clear();while(m--){int a,b,cost;scanf("%d%d%d", &a, &b, &cost);E temp;temp.next = b;temp.c = cost;edge[a].push_back(temp);temp.next = a;edge[b].push_back(temp);//无向边，所以两个点的邻接链表都要增加}for(int i = 1; i <= n; i++){Dis[i] = -1;mark[i] = false;}Dis[1] = 0;mark[1] = true;int newP = 1;//表示是上一个加入到最短路径的点for(int i = 1; i < n; i++)//循环n-1次，将所有的点都加入到集合中{for(int j = 0; j < edge[newP].size(); j++){int t = edge[newP][j].next;int ct = edge[newP][j].c;if(mark[t] == true)continue;if(Dis[t] == -1 || Dis[t] > Dis[newP] + ct)Dis[t] = Dis[newP] + ct;}int min = 100000000;for(int k = 1; k <= n; k++){if(mark[k] == true)continue;if(Dis[k] == -1)continue;if(min > Dis[k]){min = Dis[k];newP = k;}}mark[newP] = true;}printf("%d\n", Dis[n]);}return 0;
}

运行结果，最后一个例子是上面的图：

2. floyd算法求最短路径，这种算法要求事先得到所有直接相连结点间的距离，然后依次判断i,j之间是否存在一个中间结点，使得

ans[i][j] > ans[i][k] + ans[k][j]从而得到新的ans[i][j]的值，要对这个中间结点进行所有结点的遍历，不可达的要跳过，对所有ans[i][j]进行遍历n次，就可以得到所有结点间的最短距离，包括i, j之间包含多个中间结点的情况，不用深入研究，记住即可。注意设定ans[i][i] = 0,所以 ans[i][j] == ans[i][i] + ans[i][j]，不会进行更新。

代码为：

#include<cstdio>
#include<iostream>
using namespace std;int ans[101][101]; //初始值为邻接矩阵，只有直接相邻的结点的距离才有意义，否则为-1
int main()
{int n, m;while(scanf("%d%d", &n, &m) != EOF){if(n == 0 && m == 0)break;for(int i = 1; i <= n; i++){for(int j = 1; j <= n; j++){ans[i][j] = -1;}ans[i][i] = 0; //自己到自己的路径长度设为0}while(m--){int a, b, c;scanf("%d%d%d", &a, &b, &c);ans[a][b] = ans[b][a] = c;//无向图}for(int k = 1; k <= n; k++)for(int i = 1; i <= n; i++)for(int j = 1; j <= n; j++){if(ans[i][k] == -1 || ans[k][j] == -1)continue;if(ans[i][j] == -1 || ans[i][k] + ans[k][j] < ans[i][j])ans[i][j] = ans[i][k] + ans[k][j];}printf("%d\n", ans[1][n]);}return 0;
}

运行结果为：

这篇关于最短路径问题(dj和floyd算法)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---