本文主要是介绍矩阵分解ALS-交替最小二乘法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
ALS(alternating least squares)
ALS是交替最小二乘的简称。在机器学习中,ALS特指使用交替最小二乘求解的一个协同推荐算法。如:将用户(user)对商品(item)的评分矩阵分解成2个矩阵:

把原来的矩阵拆分成:

如何从评分矩阵中分解出User矩阵和Item矩阵,
- 只有左侧的评分矩阵R是已知的
- User矩阵和Item矩阵是未知
- 学习出User矩阵和Item矩阵,使得User矩阵*Item矩阵与评分矩阵中已知的评分差异最小 => 最优化问题
我们最终的目的是使求得的打分矩阵loss最小

这里讲一下算数平均值,我们做实验经常用到算数平均值,其实算数平均值最终的原理也是最小二乘法
为什么算数平均值为实际值
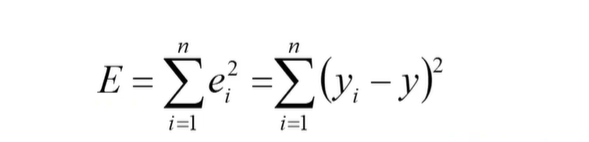
导数为0的时候为最小值,因此
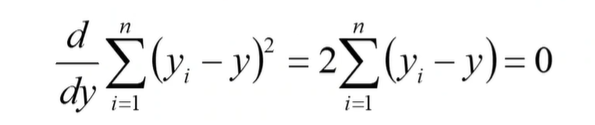
也就是:

所以:
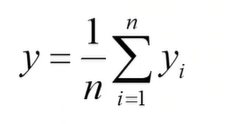
最小二乘法是一种重要的数据拟合技术
可以应用于线性回归,非线性回归
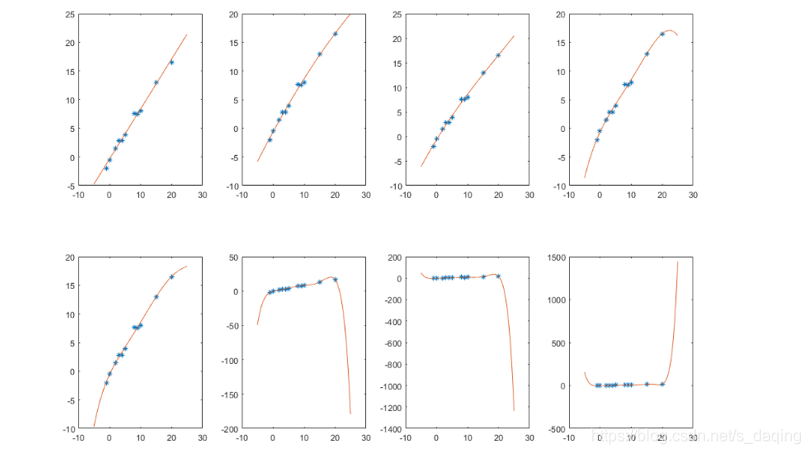
之所以叫交替最小二乘法,是因为同时求X和Y两个矩阵,所以需要固定X求Y,再固定Y求X
1、固定Y优化X
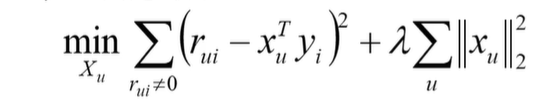
将目标函数转化为矩阵表达形式
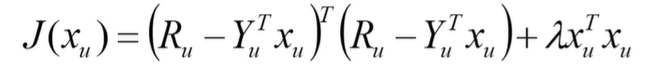
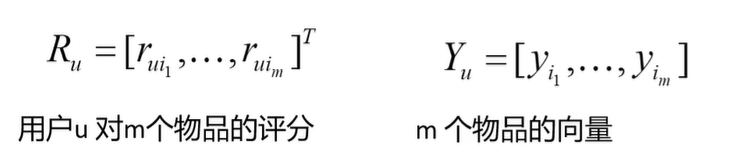
对目标函数 յ关于 xu 求梯度,并令梯度为零,得
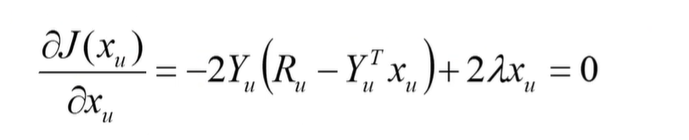
求解后,得:
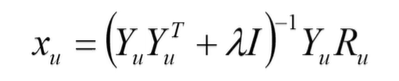
x u = ( Y u Y T + λ I ) − 1 Y u R u x_u=(Y_uY^T + \lambda I) ^{-1}Y_uR_u xu=(YuYT+λI)−1YuRu
2、固定X优化Y
同理,求解得
y i = ( X u X T + λ I ) − 1 X u R u y_i=(X_uX^T + \lambda I) ^{-1}X_uR_u yi=(XuXT+λI)−1XuRu
然后交替迭代:
- 初始化X,Y
- 利用for u=1,…,n do ∂ L o s s ( X , Y ) ∂ x u \frac{\partial^{}Loss(X, Y)}{\partial x_u^{}} ∂xu∂Loss(X,Y)=0 去得到xu
- 利用for i=1,…,m do ∂ L o s s ( X , Y ) ∂ y i \frac{\partial^{}Loss(X, Y)}{\partial y_i^{}} ∂yi∂Loss(X,Y)=0 去得到yi
- 重复2和3,不断去更新直到均方根误差RMSE收敛

这篇关于矩阵分解ALS-交替最小二乘法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



