本文主要是介绍Photometric Stereo 光度立体三维重建(一)——介绍,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在计算机视觉的三维重建中,基于几何的方法有:
- SFM立体视觉

- 结构光

我们在这篇文章中介绍的是基于光度立体视觉的三维重建方法:

基于几何的三维重建方法中可以恢复粗略的三维形状,而光度法的特点是可以对物体进行精细恢复
0. 预备知识
0.1 物体表面法向量
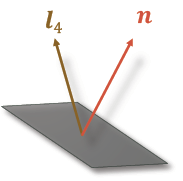
一个表面的法向量(法线)n垂直于其切平面:
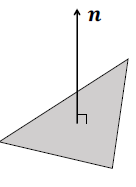
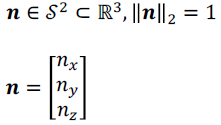
0.2 郎伯反射
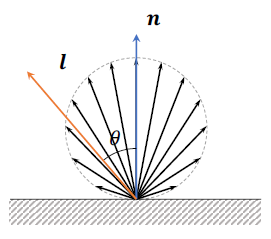
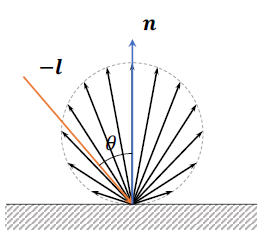
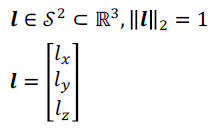
特点:
1.反射光的量与 l T n ( = c o s θ ) \ l^Tn(=cos\theta) lTn(=cosθ)成正比
2.表面亮度不取决于观察角度
更多关于郎伯表面的理论可以参考https://www.cnblogs.com/jerrycg/
0.3 有向光照模型

特点:
1.所有射线平行
2.一个无穷远的点光源
1.郎伯图像形成模型


其中:
m ∈ R + \ m \in R_+ m∈R+是测量到的像素的强度(像素值)
e ∈ R + \ e \in R_+ e∈R+是光源强度(辐射强度)
ρ ∈ R + \ \rho \in R_+ ρ∈R+是郎伯表面的漫反射率
l \ l l 是3维的单位光源位置向量
n \ n n 是3维的表面法向量
在忽略未知的缩放以及假设单位强度的光源强度后,我们可以得到简化的郎伯成像模型:

2.光度立体视觉[WoodHam80]
2.1 单个像素
对于一个像素的情况,在假设了单位反射率后,通过多次光照:
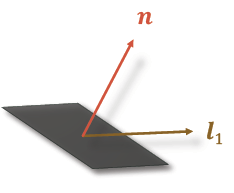
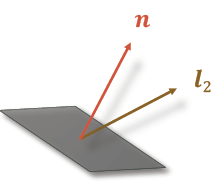
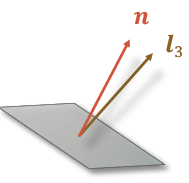
我们可以得到:

同样的,如果我们在f个光源下观察,将会得到线性方程组:

我们的目的是求出法向量n
当我们所使用的光源数为3(f=3)而且L可逆时,我们可以如此求出n:

当f>3时,方程组是超定的,我们可以使用最小二乘法来获得近似解:

2.2 多个像素
扩展到多个像素后,我们将获得的图像展开为行向量,此时我们可以得到线性方程组(其中f是图像数量(光源数量),p是一张图像的像素数量):

来求出法向量:

3. 矩阵形式的图像形成模型
m ∈ R + \ m \in R_+ m∈R+是测量到的像素的强度(像素值)
e ∈ R + \ e \in R_+ e∈R+是光源强度(辐射强度)
ρ ∈ R + \ \rho \in R_+ ρ∈R+是郎伯表面的漫反射率
l \ l l 是3维的单位光源位置向量
n \ n n 是3维的表面法向量
3.1 单像素 单光源


3.2 单像素 多光源(f个)



3.3 多像素(p) 多光源(f)



4. 外观子空间
郎伯场景的外观在没有阴影,定向光源下驻留在三维子空间
M \ \mathbf{M} M的秩总为3,也就是说,3幅基图像可以生成新的外观:


5. 问题设置
在以下的等式中,红色代表未知量
5.1 标定光度立体视觉
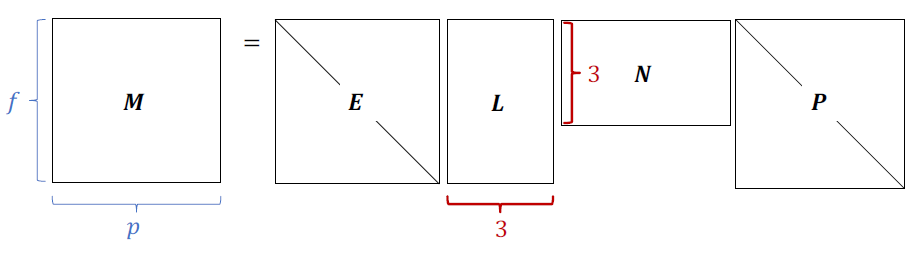
E \ E E 光源强度 L \ L L 光源方向 N \ N N 物体表面法向量 P \ P P 物体表面反射率
在已知(已标定)的光源方向和光源强度下,恢复场景形状以及反射率

问题等价于:

在f=3, L ′ \ L' L′满秩的确切情况下:

在f>3, L ′ \ L' L′满秩的超定情况下,使用最小二乘求解(不是唯一办法):

在f<3的欠定情况下,没有唯一的解
当 N ′ \ N' N′求解出来后,由于 n i \ n_i ni是单位向量,我们可以通过列归一化来求解N和P:


5.2 未标定光度立体视觉
在未标定(未知)的光源方向及强度的情况下恢复物体表面法向量及反射率

问题等价于:


我们对矩阵M进行奇异值分解:


分解在3x3的可逆线性变换A下是唯一的:

此时可以得到:
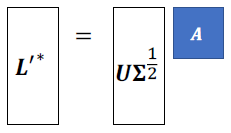
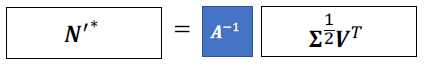
这表明有许多(无穷多)种光和物体形状的组合可以产生相同的外观(捕获到的图像M)
这里要介绍一个名词——广义浅浮雕歧义(Generalized Bas-Relief Ambiguity)[Belhumeur97]:当正交地观察一个具有郎伯表面的物体,决定其三维形状时具有隐式的歧义,物体表面通过广义浅浮雕转换后不能被辨别。对于由任意数量的遥远光源照射的物体的每一幅图像,都存在由类似的光源照射的转换后的物体的相同图像。也就是在未知的光源以及不同物体表面下可能观察到相同的现象,可以从下面两幅图像感受一下
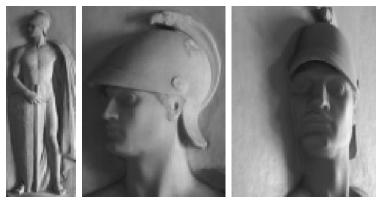

为了得到一个有效的表面,歧义性可以转化为广义浅浮雕转换(generalized bas-relief (GBR) transformation.):

5.3 半标定光度立体视觉
在已知光源方向,但光源强度未知的情况下,恢复物体表面法向量及反射率

问题等价于:


假设光的强度大于0,那么对角阵E是可逆的,等式转化为:

此时原来的双线性问题就转换成了一个线性问题
它可以写成一个 A x = 0 \ Ax=0 Ax=0的形式:

更直观一点的形式:

当 r a n k ( D ) = 3 p + f − 1 \ rank(\mathbf{D})=3p+f-1 rank(D)=3p+f−1时,上式在一个尺度缩放下具有唯一解,因此,必要条件为 p f ≥ 3 p + f − 1 \ pf \geq 3p+f-1 pf≥3p+f−1,即 ( p − 1 ) ( f − 3 ) ≥ 2 \ (p-1)(f-3) \geq 2 (p−1)(f−3)≥2,也就是说至少需要4个光源,两个具有不同表面法向量的像素
对于这种情况,我们可以使用交替最小化来求解(迭代过程中对E适当正则化):

6.总结
| 标定 | 未标定 | 半标定 | |
|---|---|---|---|
| 表面法向量及反射率 | 未知 | 未知 | 未知 |
| 光源方向 | 已知 | 未知 | 已知 |
| 光源强度 | 已知 | 未知 | 未知 |
| 唯一解条件 | 光源数>3 | 除非引入外部假设,不然无解 | 光源>4,像素>2 |

我组建了一个光度立体技术的交流群,有兴趣的朋友可以一起来讨论一下!

这篇关于Photometric Stereo 光度立体三维重建(一)——介绍的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





