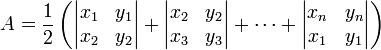覆盖的面积扫描线

本文主要是介绍覆盖的面积扫描线，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

//魔改线段树的做法，想了好久注意是那个一次用len记录，两次用length来计数
#include<iostream>
#include<cstdio>
#include<string.h>
#include<algorithm>
using namespace std;
const int maxn=2*1010;
struct tree{double l,r,len,length;int lazy,vis;
}t[maxn<<3];
double val[maxn];
int vis[maxn<<3];
struct node{double x,y1,y2;int flag;bool operator<(node a) const{return x<a.x;}
}p[maxn];//扫描线 
void build(int p,int l,int r)//浮点数 
{t[p].l=val[l],t[p].r=val[r];if(r-l<=1){vis[p]=1;//结束的标志 return;}int mid=l+r>>1;build(p<<1,l,mid);build(p<<1|1,mid,r);
}
void spread(int p)
{if(t[p].lazy>=2)	{t[p].length=t[p].r-t[p].l;//一次的长度为0 t[p].len=0;}else if(t[p].lazy==1)	{if(vis[p])t[p].len=t[p].r-t[p].l,t[p].length=0;//如果是最后的边的话他就是直接一次的长度为r-l，加上一个为0，防止最后一个从2变为1后会有变化 double all=t[p].r-t[p].l;t[p].length=t[p<<1].length+t[p<<1|1].length+t[p<<1].len+t[p<<1|1].len;//两次的长度为原本下方的两次和一次t[p].len=all-t[p].length;	}else {t[p].len=t[p<<1].len+t[p<<1|1].len;t[p].length=t[p<<1].length+t[p<<1|1].length;//这里不需要考虑到最后的时候下标越界，因为最后一个有放回的时候 } 
}
void modify(int p,double l,double r,int w)
{if(t[p].l>=l&&t[p].r<=r){t[p].lazy+=w;spread(p);return;}if(t[p<<1].r>l)//注意没有等号的话会死循环 modify(p<<1,l,r,w);if(t[p<<1|1].l<r)modify(p<<1|1,l,r,w);spread(p);
}
int main(){int T,n;scanf("%d",&T);for(int i=1;i<=T;i++){int cnt=0;double ans=0;memset(val,0,sizeof val);memset(t,0,sizeof t);memset(p,0,sizeof p);memset(vis,0,sizeof vis);scanf("%d",&n);double x1,y1,x2,y2;for(int j=1;j<=n;j++){scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);p[j*2-1]=(node){x1,y1,y2,1};p[j*2]=(node){x2,y1,y2,-1};val[++cnt]=y1,val[++cnt]=y2; }sort(val+1,val+1+cnt);sort(p+1,p+1+cnt);build(1,1,cnt);for(int j=1;j<cnt;j++){modify(1,p[j].y1,p[j].y2,p[j].flag);
//			for(int k=1;k<=31;k++)
//				cout<<k<<"  aaa "<<t[k].l<<"   "<<t[k].r<<"  "<<t[k].lazy<<"  "<<t[k].len<<endl;ans+=(p[j+1].x-p[j].x)*t[1].length; }printf("%.2f\n",ans);}return 0;
}

这篇关于覆盖的面积扫描线的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---