AcWing 344 观光之旅

题目描述：

给定一张无向图，求图中一个至少包含3个点的环，环上的节点不重复，并且环上的边的长度之和最小。

该问题称为无向图的最小环问题。

你需要输出最小环的方案，若最小环不唯一，输出任意一个均可。

输入格式

第一行包含两个整数N和M，表示无向图有N个点，M条边。

接下来M行，每行包含三个整数u，v，l，表示点u和点v之间有一条边，边长为l。

输出格式

输出占一行，包含最小环的所有节点（按顺序输出），如果不存在则输出’No solution.’。

数据范围

1≤N≤100,
1≤M≤10000,
1≤l<500

输入样例：

5 7
1 4 1
1 3 300
3 1 10
1 2 16
2 3 100
2 5 15
5 3 20

输出样例：

1 3 5 2

分析：

本题考察floyd算法求最小环，并且要求输出最小环中所有的节点。

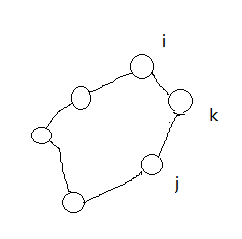
如图所示，设环上编号最大的节点编号是k，i和j分别是环上与k相邻的两个节点。根据之前对floyd算法的推导，f[k][i][j]表示图上i经过编号不超过k的节点到达j的最短路径长度，观察上图可以发现，环的长度等于i到j的最短距离加上g[i][k]再加上g[k][j]，设环的长度为ans，则ans = f[i][j] + g[i][k] + g[k][j]，这里的f[i][j]是对f[k-1][i][j]降维后的结果，为什么是f[k-1][i][j]而不是f[k][i][j]，因为前面已经规定k是最大的节点，环上其他的节点必然都小于k。为什么要这么规定，这种思路是如何来的？后面会分析这种思路的由来。

我们知道，floyd算法最外层k刚刚循环到第k次时，f[i][j]存储的还是i经过编号不超过k-1的节点到达j的最短路径长度，此时的f[i][j]正是我们所需要的，因此在第k次循环开始时，由k，i，j加上i到j中间的节点构成的最小环长度就是f[i][j] + g[i][k] + g[k][j]，我们还是用三层循环去枚举所有的情况，最终就可以求出最小环的长度。

for(int k = 1;k <= n;k++){for(int i = 1;i < k;i++){for(int j = i + 1;j < k;j++){if((ll)f[i][j] + g[i][k] + g[k][j] < ans){ans = f[i][j] + g[i][k] + g[k][j];cnt = 0;path[cnt++] = k,path[cnt++] = i;get_path(i,j);path[cnt++] = j;}}}for(int i = 1;i <= n;i++){for(int j = 1;j <= n;j++){if(f[i][k] + f[k][j] < f[i][j]){f[i][j] = f[i][k] + f[k][j];pos[i][j] = k;}}}}

上面是求最小环的核心代码，暂且不去看用来求环上所有节点的get_path的部分， 如果直接按照前面分析的思路去求解，想到的肯定是第一层循环k从1到n，第二三层是i，j从1到n，然后最内层先更新下最小环长度，在用floyd算法更新f[i][j]。而看到上面的代码肯定会有疑问，为什么要将最内层的两个循环分开写？问题的答案是为了提高效率，这背后的原因值得深思。如果一开始我们就按照floyd算法的习惯去进行状态表示，用f[k][i][j]表示以相邻的三点i，j，k以及i与j之间编号不超过k的节点构成的最小环长，也就是说，仅要求i到j中间的节点小于k，i，j与k的大小关系不明确规定，自然就可以按照floyd的写法三层循环都从1循环到n。这样写一方面需要判断i、j不能等于k，否则会违反环上至少三个点的规定；另一方面效率较低，我们直接选k作为环上最大的节点，图中任意一个环总有最大编号的节点，这是毫无疑问的，并且环上与k相邻的两点必然都小于k并且互不相等，这就保证了这种状态定义和实现对各种环状态转移的没有遗漏了。另一个问题是floyd算法能否也写成这样呢？第二三层循环的上限都设置为k-1，如果这样实现，floyd算法的状态表示就需要修改为f[k][i][j]表示从i到j包含i，j在内所有点编号都不超过k的最小路径长度，这样表示显然是不合理的，比如从任何点到n的最小距离我们就无法找到一个比n更大的中间点来作为k更新距离。

再来看记录最小环上节点的代码，在循环中，我们知道环上已经有i，j，k三点，只需要再存储下i到j的最短路径上节点的编号即可，如果i到j的最短路径经过了中间点k，那么i到j最短路径上的节点就被分为了三部分：i到k，k，k到j。问题的规模就缩小了，这就意味着可以递归的求解最短路径上的节点。还有个容易忽略的点就是每次最小环长被更新时都需要计算下此时环上有哪些节点，而不能仅仅是记录下此时的i，j，k，在算法结束后再计算，其中的原因求i到j最短路径上节点时用到了i到j的中间节点k，我们用pos[i][j]=k存储了此时最小环中i到j的中间节点k，但是随着k的递增，pos[i][j]的值也会不停地改变，等到算法结束时的pos[i][j]早已经不是最小环时候的k了。总的代码如下：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 105,INF = 0x3f3f3f3f;
int g[N][N],f[N][N],pos[N][N],path[N];
int m,n,cnt = 0;
void get_path(int i,int j){if(!pos[i][j])  return;get_path(i,pos[i][j]);path[cnt++] = pos[i][j];get_path(pos[i][j],j);
}
int main(){scanf("%d%d",&n,&m);int a,b,c;memset(g,0x3f,sizeof g);for(int i = 1;i <= n;i++)   g[i][i] = 0;for(int i = 0;i < m;i++){scanf("%d%d%d",&a,&b,&c);g[a][b] = g[b][a] = min(g[a][b],c);//防重边}memcpy(f,g,sizeof g);int ans = INF;for(int k = 1;k <= n;k++){for(int i = 1;i < k;i++){for(int j = i + 1;j < k;j++){if((ll)f[i][j] + g[i][k] + g[k][j] < ans){//防溢出ans = f[i][j] + g[i][k] + g[k][j];cnt = 0;path[cnt++] = k,path[cnt++] = i;get_path(i,j);path[cnt++] = j;}}}for(int i = 1;i <= n;i++){for(int j = 1;j <= n;j++){if(f[i][k] + f[k][j] < f[i][j]){f[i][j] = f[i][k] + f[k][j];pos[i][j] = k;}}}}if(ans == INF)  puts("No solution.");else{for(int i = 0;i < cnt;i++){printf("%d ",path[i]);}puts("");}return 0;
}