力扣--从前序与中序遍历序列构造二叉树

本文主要是介绍力扣--从前序与中序遍历序列构造二叉树，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目：

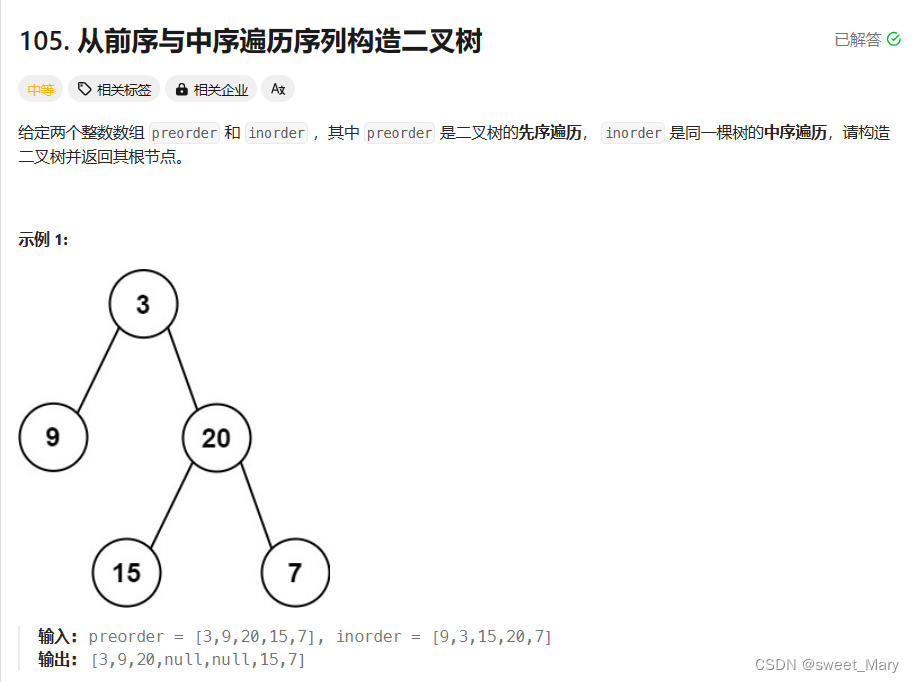
思想：

首先先序遍历能确定根节点的值，此时查看该值在中序遍历中的位置（如果索引为i），那么i左侧为左子树，i 右侧为右子树。从中序数组中即可看出左子树结点个数为 i，右子树节点个数为inorder.size()-i-1。也就代表先序数组中除了第一个元素外，先 i 个元素是左子树对应的先序数组元素，后面的元素为右子树对应的先序数组元素。递归的形式就出现啦！如果没想到可以看一下函数的参数。

代码如下：

C++：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {if(preorder.size()==0){return nullptr;}TreeNode* head=new TreeNode;head->val=preorder[0];int idx=find(inorder.begin(),inorder.end(),preorder[0])-inorder.begin();//preorder---左子树vector<int>::const_iterator Firstprel=preorder.begin()+1;vector<int>::const_iterator Secondprel=preorder.begin()+idx+1;vector<int> prel;prel.assign(Firstprel,Secondprel);//preorder---右子树vector<int>::const_iterator Firstprer=preorder.begin()+idx+1;vector<int>::const_iterator Secondprer=preorder.end();vector<int> prer;prer.assign(Firstprer,Secondprer);//inorder---左子树vector<int>::const_iterator Firstinl=inorder.begin();vector<int>::const_iterator Secondinl=inorder.begin()+idx;vector<int> inl;inl.assign(Firstinl,Secondinl);//inorder---右子树vector<int>::const_iterator Firstinr=inorder.begin()+idx+1;vector<int>::const_iterator Secondinr=inorder.end();vector<int> inr;inr.assign(Firstinr,Secondinr);head->left=buildTree(prel,inl);head->right=buildTree(prer,inr);return head;}
};

注意看一下这里的写法：

int idx=find(inorder.begin(),inorder.end(),preorder[0])-inorder.begin();

参考博文：（在inorder中寻找preorder[0]这个元素，返回其索引值）

c++vector查找元素所在的索引下标_vector查找元素索引-CSDN博客

//preorder---左子树
vector<int>::const_iterator Firstprel=preorder.begin()+1;
vector<int>::const_iterator Secondprel=preorder.begin()+idx+1;
vector<int> prel;
prel.assign(Firstprel,Secondprel);

参考博文：（就是把preorder中的第一个元素直到第idx个元素，复制给prel）

vector 切片，截取指定区间元素_vector截取-CSDN博客

Python：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:if len(preorder)==0:return Nonehead=TreeNode(preorder[0])idx=inorder.index(preorder[0])prel=preorder[1:idx+1]prer=preorder[idx+1:]inl=inorder[:idx+1]inr=inorder[idx+1:]head.left=self.buildTree(prel,inl)head.right=self.buildTree(prer,inr)return head

注意这样几个写法：

Python中的空指针为None

Python中的创建实例