光线追踪10 - Dielectrics（ 电介质 ）

本文主要是介绍光线追踪10 - Dielectrics（ 电介质 ），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

水、玻璃和钻石等透明物质都属于电介质。当光线射入这些物质时，会分为反射光线和折射（透射）光线。我们将通过随机选择反射或折射来处理这一现象，每次相互作用只生成一条散射光线。

11.1 Refraction
 最难调试的部分是折射光线。通常情况下，如果存在折射光线，我会首先让所有光线都发生折射。对于这个项目，我尝试在场景中放置了两个玻璃球，结果如下（我还没有告诉你如何正确或错误地完成它，但很快会告诉你！）：

Image 15: Glass first

这是正确的吗？在现实生活中，玻璃球看起来很奇怪。但不，这不正确。世界应该被颠倒过来，而且没有奇怪的黑色物体。我只是将光线直接打印在图像的中间，显然是错误的。这种方法通常能够解决问题。

11.2 Snell's Law
折射现象可由斯涅尔定律描述：
η⋅sinθ=η′⋅sinθ′
其中θ和θ′是相对于法线的角度，η和η′（pronounced “eta” and “eta prime”）是折射率（一般情况下，空气为1.0，玻璃为1.3-1.7，钻石为2.4）。几何关系如下图所示：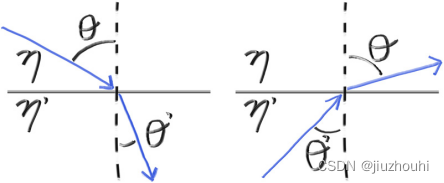

Figure 17: Ray refraction

为了确定折射光线的方向，我们需要解出sinθ'：
sinθ′=(η/η′)⋅sinθ

    在折射面的一侧，存在一条折射光线R'和一条法线n'，它们之间存在一个角度θ'。我们可以将R'分为垂直于n'的部分和平行于n'的部分：R′=R′⟂+R′||
如果我们解出 R′⟂和 R′||，我们得到：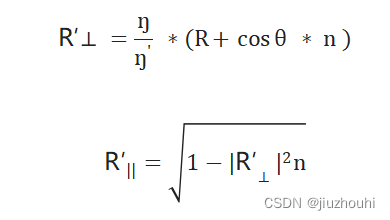

    如果你愿意，你可以自己去证明这一点，但我们将把它视为事实并继续。本书的其余部分不需要你理解这个证明。我们知道右侧每一项的值，除了cosθ。众所周知，两个向量的点积可以用它们之间夹角的余弦来解释：
a⋅b=|a||b|cosθ
如果我们将向量a和b限制为单位向量：
a⋅b=cosθ
现在我们可以用已知量重写R'⊥：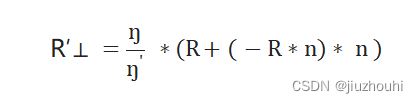


当我们将它们重新组合在一起时，我们可以编写一个函数来进行计算R'

...
inline vec3 reflect(const vec3& v, const vec3& n) {
return v - 2*dot(v,n)*n;
}inline vec3 refract(const vec3& uv, const vec3& n, double etai_over_etat) {
auto cos_theta = fmin(dot(-uv, n), 1.0);
vec3 r_out_perp =  etai_over_etat * (uv + cos_theta*n);
vec3 r_out_parallel = -sqrt(fabs(1.0 - r_out_perp.length_squared())) * n;
return r_out_perp + r_out_parallel;
}

Listing 65: [vec3.h] Refraction function

而那种经常发生折射的介质是：

...
class metal : public material {
...
};class dielectric : public material {public:
dielectric(double index_of_refraction) : ir(index_of_refraction) { }bool scatter(const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered) const override {attenuation = color(1.0, 1.0, 1.0);double refraction_ratio = rec.front_face ? (1.0/ir) : ir;vec3 unit_direction = unit_vector(r_in.direction());vec3 refracted = refract(unit_direction, rec.normal, refraction_ratio);scattered = ray(rec.p, refracted);return true;}
private:double ir; // Index of Refraction
};

Listing 66: [material.h] Dielectric material class that always refracts

现在我们将更新场景，将左侧和中间的球体改为玻璃材质：

auto material_ground = make_shared<lambertian>(color(0.8, 0.8, 0.0));
auto material_center = make_shared<dielectric>(1.5);
auto material_left = make_shared<dielectric>(1.5);
auto material_right  = make_shared<metal>(color(0.8, 0.6, 0.2), 1.0);

Listing 67: [main.cc] Changing left and center spheres to glass

得到如下：

Image 16: Glass sphere that always refracts


11.3  Total Internal Reflection（全反射）
那看起来肯定是不对的。一个麻烦的实际问题是，当光线处于折射率较高的介质中时，斯涅尔定律没有真实解，因此无法发生折射。如果我们回顾一下斯涅尔定律和sinθ′的推导过程：
sinθ′=(η/η′)⋅sinθ
    如果光线在玻璃内部，外部是空气(η=1.5,η′=1.0):
sinθ′=(1.5/1.0)⋅sinθ
sinθ′的值不能大于1。因此，如果...
（1.5/1.0)⋅sinθ>1.0
方程两边的等式被打破，无法存在解。如果没有解，光就无法折射，因此必须反射光线：

if (refraction_ratio * sin_theta > 1.0) {
// Must Reflect...
} 
else {
// Can Refract...
}

Listing 68: [material.h] Determining if the ray can refract

在这种情况下，所有光线都被反射回来，因为通常是在固体物体内部发生的，所以被称为“全内反射”。这就是为什么有时候当你在水下时，水和空气的边界会像一个完美的镜子一样反射光线。

我们可以使用三角函数的性质来求解sin_theta：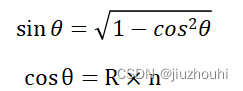

double cos_theta = fmin(dot(-unit_direction, rec.normal), 1.0);
double sin_theta = sqrt(1.0 - cos_theta*cos_theta);
if (refraction_ratio * sin_theta > 1.0) {
// Must Reflect
...
}
else {
// Can Refract
...
}

Listing 69: [material.h] Determining if the ray can refract


并且总是（当可能时）发生折射的介质是：

class dielectric : public material {public:
dielectric(double index_of_refraction) : ir(index_of_refraction) {}bool scatter(const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered)const override {attenuation = color(1.0, 1.0, 1.0);double refraction_ratio = rec.front_face ? (1.0/ir) : ir;vec3 unit_direction = unit_vector(r_in.direction());double cos_theta = fmin(dot(-unit_direction, rec.normal), 1.0);double sin_theta = sqrt(1.0 - cos_theta*cos_theta);bool cannot_refract = refraction_ratio * sin_theta > 1.0;vec3 direction;if (cannot_refract) direction = reflect(unit_direction, rec.normal);elsedirection = refract(unit_direction, rec.normal, refraction_ratio);scattered = ray(rec.p, direction);return true;
}
private:    double ir; // Index of Refraction
};

Listing 70: [material.h] Dielectric material class with reflection

衰减始终为1——玻璃表面不吸收任何东西。如果我们使用这些参数进行尝试：

auto material_ground = make_shared<lambertian>(color(0.8, 0.8, 0.0));
auto material_center = make_shared<lambertian>(color(0.1, 0.2, 0.5));
auto material_left = make_shared<dielectric>(1.5);
auto material_right = make_shared<metal>(color(0.8, 0.6, 0.2), 0.0);

Listing 71: [main.cc] Scene with dielectric and shiny sphere

从而得到

Image 17: Glass sphere that sometimes refracts

11.4 Schlick Approximation 希克近似
现实玻璃的反射率随角度变化而不同 - 当以陡峭的角度看窗户时，它会变成镜子。有一个复杂的方程可以描述这种变化，但几乎每个人都使用克里斯托夫·希克（Christophe Schlick）提供的便宜且令人惊讶地准确的多项式近似。这可以得到我们完整的玻璃材质：

class dielectric : public material {public:
dielectric(double index_of_refraction) : ir(index_of_refraction) {}bool scatter(const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered)const override {attenuation = color(1.0, 1.0, 1.0);double refraction_ratio = rec.front_face ? (1.0/ir) : ir;vec3 unit_direction = unit_vector(r_in.direction());double cos_theta = fmin(dot(-unit_direction, rec.normal), 1.0);double sin_theta = sqrt(1.0 - cos_theta*cos_theta);bool cannot_refract = refraction_ratio * sin_theta > 1.0;vec3 direction;if (cannot_refract || reflectance(cos_theta, refraction_ratio) > random_double())direction = reflect(unit_direction, rec.normal);elsedirection = refract(unit_direction, rec.normal, refraction_ratio);scattered = ray(rec.p, direction);return true;}private:    double ir; // Index of Refractionstatic double reflectance(double cosine, double ref_idx) {// Use Schlick's approximation for reflectance.auto r0 = (1-ref_idx) / (1+ref_idx);r0 = r0*r0;return r0 + (1-r0)*pow((1 - cosine),5);}
};

Listing 72: [material.h] Full glass material


11.5 Modeling a Hollow Glass Sphere(建模一个空心玻璃球)
使用介电球体的一个有趣且简单的技巧是注意到，如果使用负半径，几何形状不受影响，但表面法线指向内部。这可以用作一个气泡来制作空心玻璃球：

...
world.add(make_shared<sphere>(point3( 0.0, -100.5, -1.0), 100.0, material_ground));
world.add(make_shared<sphere>(point3( 0.0,    0.0, -1.0),   0.5, material_center));
world.add(make_shared<sphere>(point3(-1.0,    0.0, -1.0),   0.5, material_left));
world.add(make_shared<sphere>(point3(-1.0,    0.0, -1.0),  -0.4, material_left));
world.add(make_shared<sphere>(point3( 1.0,    0.0, -1.0),   0.5, material_right));
...

Listing 73: [main.cc] Scene with hollow glass sphere


得到效果

Image 18: A hollow glass sphere
 

这篇关于光线追踪10 - Dielectrics（ 电介质 ）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---