本文主要是介绍SSD LDPC纠错算法的重要性,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
固态硬盘(Solid State Drives, SSD)作为计算机行业中最具革命性的技术之一,凭借其更快的读写速度、增强的耐用性和能效,已经成为大多数用户的首选存储方案。然而,如同任何其他技术一样,SSD也面临自身的挑战,其中首要问题之一便是数据可靠性。由于电源故障、电压波动以及磨损和老化等因素,存储在SSD中的数据可能会遭到破坏。
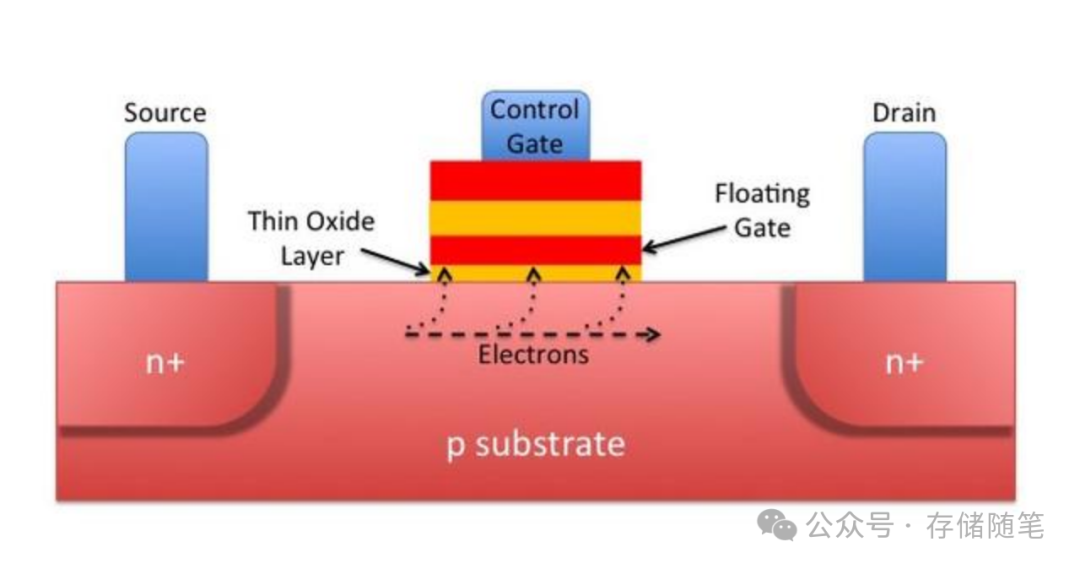
SSD的存储介质是什么,它就是NAND闪存。那你知道NAND闪存是怎么工作的吗?其实,它就是由很多个晶体管组成的。这些晶体管里面存储着电荷,代表着我们的二进制数据,要么是“0”,要么是“1”。NAND闪存原理上是一个CMOS管,有两个栅极,一个是控制栅极(Control Gate), 一个是浮栅(Floating Gate). 浮栅的作用就是存储电荷,而浮栅与沟道之间的氧化层(Oxide Layer)的好坏决定着浮栅存储电荷的可靠性,也就是NAND闪存的寿命。
为了应对这一问题,SSD采用了一种名为低密度奇偶校验码(Low-Density Parity-Check, LDPC)的技术。本文将深入探讨LDPC在SSD中的重要性。
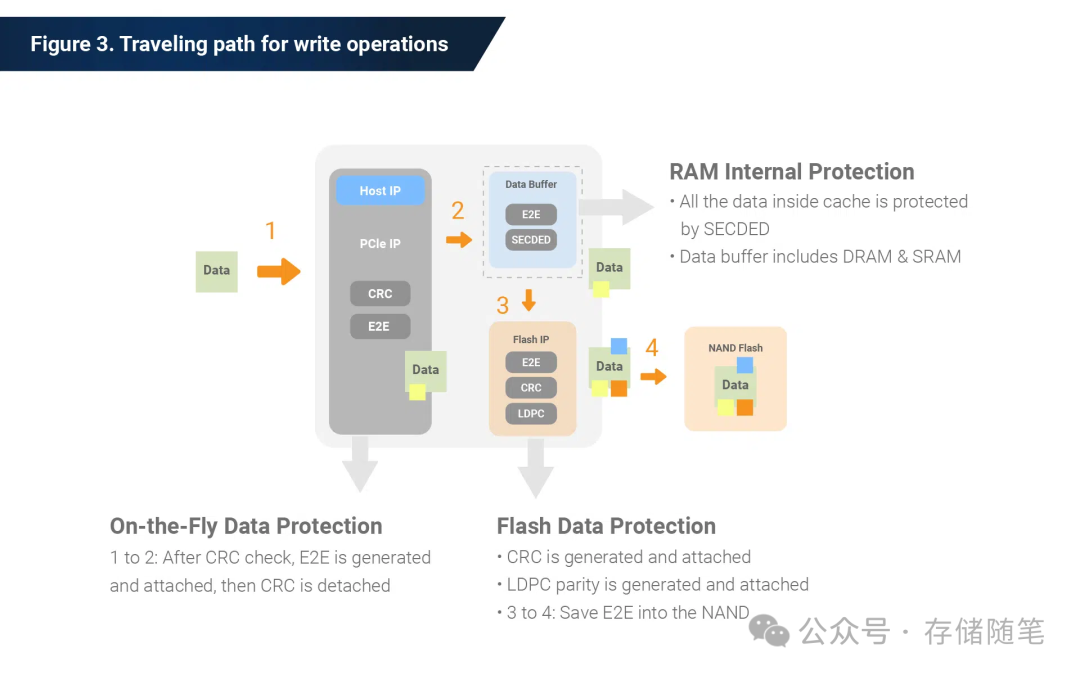
我们看下,host数据到落入NAND要经过的过程。
-
1/2步会进行CRC/E2E校验写入缓存。
-
3/4步有闪存控制器Flash IP进行E2E/CRC LDPC编码后写入NAND。
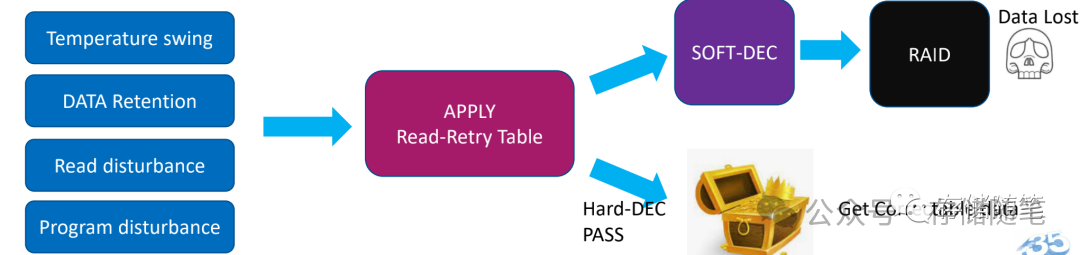
读写之间的温度差、Data Retention、读干扰、写干扰等,导致出现数据翻转,需要启动Read Retry重读机制、LDPC纠错、RAID纠错等修复机制。
纠错码是一种用于检测和纠正数据传输过程中出现的错误的技术。它们在固态硬盘(SSD)中扮演着关键角色,因为NAND闪存介质具有内在的不稳定性,容易受到各种因素的影响,如读取噪声、编程/擦除过程中的磨损等。BCH(Bose-Chaudhuri-Hocquenghem)和LDPC(Low Density Parity Check)是两种常见的纠错编码技术。
BCH(Bose-Chaudhuri-Hocquenghem)纠错码
BCH码是由印度数学家J. R. Bose和D. K. Ray-Chaudhuri以及加拿大工程师W. W. Peterson独立发现的一种线性分组码。BCH码的特点是在编码时引入了校验位,这些校验位可以根据原始数据计算得出,以确保接收端能够检测并纠正特定数量的比特错误。BCH码的优势在于其相对简单的硬件实现,但在纠错能力上不如LDPC码。
LDPC(Low Density Parity Check)纠错码
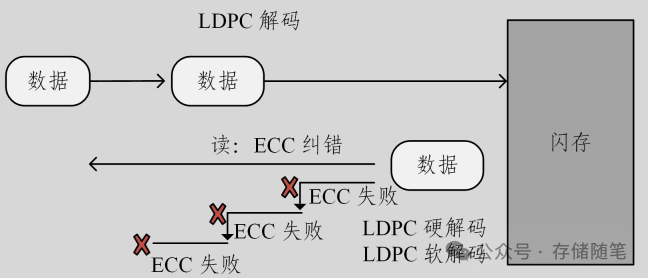
LDPC码是一种基于稀疏矩阵的纠错码,它由一组奇偶校验方程组成,其中大部分元素为零,因此得名“低密度”。LDPC码的优点是可以有效地纠正大量的错误,尤其是对于高密度存储设备来说。LDPC解码可以分为硬解码和软解码两种方式。
-
LDPC Hard Decode:硬解码是最基本的LDPC解码方法,它试图从接收到的数据中恢复正确的信息。这个过程通常涉及到将接收到的代码字与一个预定义的校验矩阵相乘,并检查结果是否为全零向量。如果是全零向量,则说明接收到的信息是正确的;否则,需要进行错误定位和纠正。比BCH更复杂,能处理更多的错误,但仍然没有充分利用信号质量信息。
-
LDPC Soft Decode:软解码是一种更复杂的解码方式,它考虑到了接收信号的质量,并尝试优化解码决策。在这个过程中,不仅使用了接收到的比特值(0或1),还考虑了每个比特的概率分布。通过这种方法,软解码可以提供更高的错误检测和纠正能力,但需要更多的计算资源。最复杂但也最强力的纠错方式,利用了信号强度信息来提高解码准确性,但需要更多的计算资源。
三者的纠错能力对比:BCH与LDPC Hard Decode纠错能力差不多,LDPC Hard Decode也只是比BCH高一点。但是,LDPC Soft Decode纠错能力会提升3倍以上。
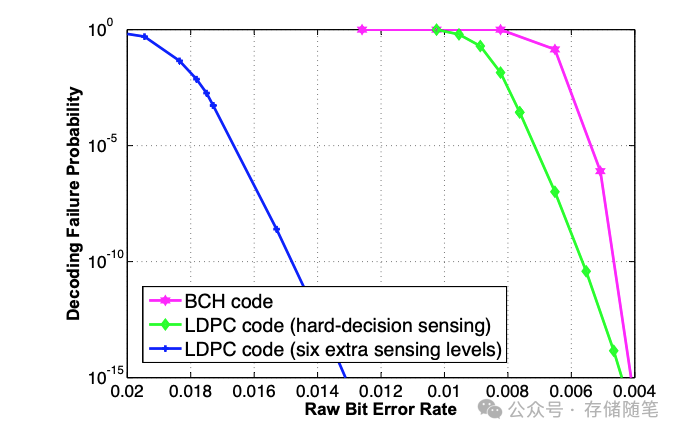
在SSD读取过程中,LDPC纠错的顺序通常是这样的:先执行硬判决解码,硬判决解码失败或者无法纠正所有错误,SSD会接着尝试使用软判决解码。软判决解码利用了每个比特的概率信息,能够更准确地定位和修复错误。
这篇关于SSD LDPC纠错算法的重要性的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









