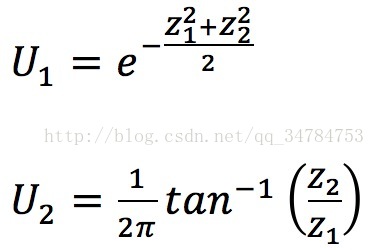1.椒盐噪声
Mat dstImage = srcImage.clone();for (int k = 0; k < n; k++){//随机取值行列int i = rand() % dstImage.rows;int j = rand() % dstImage.cols;//图像通道判定if (dstImage.channels() == 1){dstImage.at<uchar>(i, j) = 255; //盐噪声 }else{dstImage.at<Vec3b>(i, j)[0] = 255;dstImage.at<Vec3b>(i, j)[1] = 255;dstImage.at<Vec3b>(i, j)[2] = 255;}}for (int k = 0; k < n; k++){//随机取值行列int i = rand() % dstImage.rows;int j = rand() % dstImage.cols;//图像通道判定if (dstImage.channels() == 1){dstImage.at<uchar>(i, j) = 0; //椒噪声 }else{dstImage.at<Vec3b>(i, j)[0] = 0;dstImage.at<Vec3b>(i, j)[1] = 0;dstImage.at<Vec3b>(i, j)[2] = 0;}}
2.高斯噪声
高斯噪声是指高绿密度函数服从高斯分布的一类噪声。特别的,假设一个噪声,它的幅度分布服从高斯分布,而它的功率谱密度有事均匀分布的,则称这个噪声为高斯白噪声。
高斯白噪声二阶矩不相关。一阶矩为常数,是指先后信号在时间上的相关性。高斯噪声包含热噪声和三里噪声。
高斯噪声万有由它的事变平均值和两瞬时的协方差函数来确定,若噪声是平稳的。则平均值与时间无关,而协方差函数则变成仅和所考虑的两瞬时之差有关的相关函数。在意义上它等同于功率谱密度。高斯早生能够用大量独立的脉冲产生,从而在不论什么有限时间间隔内。这些脉冲中的每个买充值与全部脉冲值得总和相比都可忽略不计。
依据Box-Muller变换原理,建设随机变量U1、U2来自独立的处于(0,1)之间的均匀分布,则经过以下两个式子产生的随机变量Z0。Z1服从标准高斯分布。
上式中Z0,Z1满足正态分布,当中均值为0,方差为1,变量U1和U2能够改动为下式:
#define TWO_PI 6.2831853071795864769252866 double generateGaussianNoise() { static bool hasSpare = false; static double rand1, rand2; if(hasSpare) { hasSpare = false; return sqrt(rand1) * sin(rand2); } hasSpare = true; rand1 = rand() / ((double) RAND_MAX); if(rand1 < 1e-100) rand1 = 1e-100; rand1 = -2 * log(rand1); rand2 = (rand() / ((double) RAND_MAX)) * TWO_PI; return sqrt(rand1) * cos(rand2); }
void AddGaussianNoise(Mat& I) { // accept only char type matrices CV_Assert(I.depth() != sizeof(uchar)); int channels = I.channels(); int nRows = I.rows; int nCols = I.cols * channels; if(I.isContinuous()){ nCols *= nRows; nRows = 1; } int i,j; uchar* p; for(i = 0; i < nRows; ++i){ p = I.ptr<uchar>(i); for(j = 0; j < nCols; ++j){ double val = p[j] + generateGaussianNoise() * 128; if(val < 0) val = 0; if(val > 255) val = 255; p[j] = (uchar)val; } } }