文献阅读--Pulse-Width Modulation

本文主要是介绍文献阅读--Pulse-Width Modulation，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

《Dynamics and Control of Switched Electronic Systems》Jian Sun – Chapter 2 《Pulse-Width Modulation》

  说明： 文献中的PWM是作为电控系统中基本控制信号去介绍的，但文中对PWM信号的数学证明是同样适用于通信领域的脉宽调制PDM的，文献中也提到了使用的二重傅里叶展开分析PWM的方法最早应用于通信领域。

一、PWM基本形式

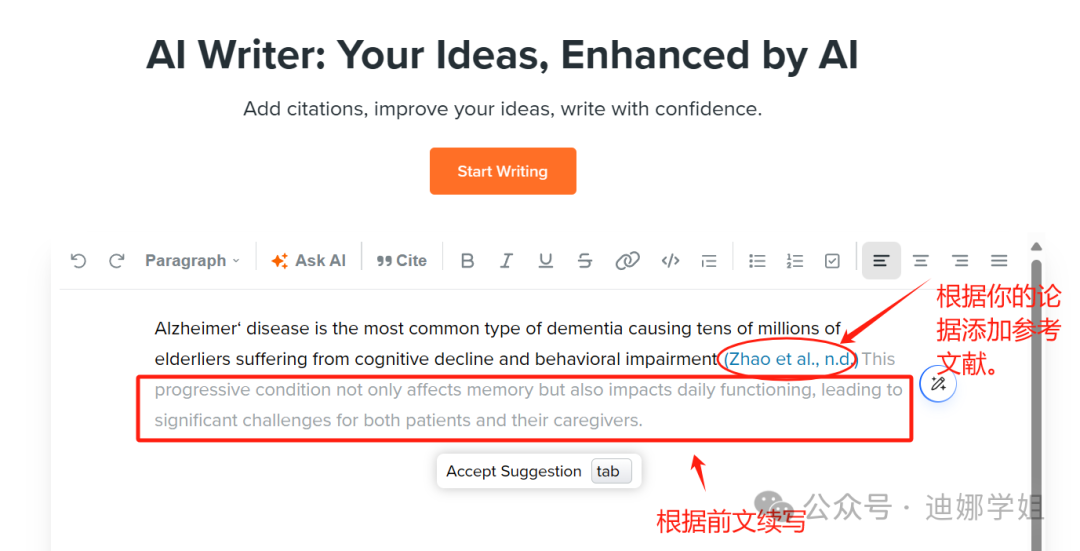
   脉宽调制可以采取不同的形式，在定义PWM方法时，脉冲频率是最重要的参数之一，可以是恒定的，也可以是可变的。如图所示，可以简单地通过比较参考信号r(t)和载波信号c(t)来产生恒定频率(CF)PWM信号，本文主要讨论CF-PWM信号。

二进制PWM输出可以用数学方法写成：
$$b_{pwm}(t)=sgn[r(t)-c(t)]$$

1.1 恒定频率(CF)PWM信号常见的三种形式：

1. 锯齿载波，如图所示：PWM输出的前导（上升）沿在固定时刻出现，而后导（下降）沿的位置为随着参考信号电平的变化而调制。因此，该方法也称为恒频后沿调制。三角波计数从0开始递增，N时重置为0同时PWM上升沿出现。
   
2. 倒锯齿载波，如图所示：PWM输出的后沿（下降）出现在固定的时刻，而前沿（上升）的位置随着参考信号电平的变化而调制。 这种方法通常被称为恒频前沿调制。三角波计数从N(最大计数值)开始递减，0时重置为N同时PWM的下降沿出现。
   
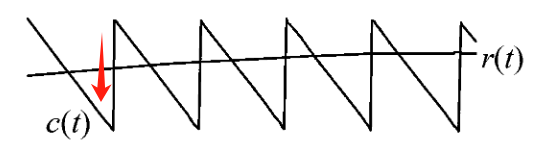
3. 三角形载波，如图所示：PWM输出的前沿和后沿都被调制。三角形的上升沿和下降沿通常是对称的，因此当参考常数为常数时，脉冲集中在载波周期内。这种方法称为恒频双沿调制。
   

二、PWM二维表示

  本节的目的是获得描述每种载波信号时PWM输出频谱的解析模型，利用该模型即可从数学角度对各种PWM应用进行频谱分析。

假定参考信号r(t) 一般由DC和单频正弦分量组成：
$$r(t)=R_0+R_{1}cos(2\pi f_{1}t+{\theta }_1).$$ 振幅R0和R1中的都可以根据所研究的具体应用设置为零。如果需要，额外的谐波也可包含在公式中。

   如果频率比$f_c/f_1$是有理数 ，则PWM波形是周期性的，可用傅立叶级数进行表示。在fc是f1的倍数的特殊情况下，可以在$1/f_1$的时间间隔内，对PWM波形执行傅立叶分析。然而，即使在这种特殊情况下，执行傅立叶分析也较为复杂，因为PWM波形中的每个开关点都由三角方程定义。该三角方程则由定义的正弦基准和表示载波信号的线性时间函数决定。 这种方程只能用数值求解，傅立叶分析结果将特定于所分析的情况，如果涉及的任何参数发生变化，则重新推导不具有一般性。在更可能的情况下，载波频率不是参考基频的倍数，傅立叶分析必须在对应于多个基频周期的区间内进行，这使得数值问题变得难以解决。
  为解决上述问题，引入一个新的二维函数，而不是涉及两个不同频率的原始时间函数去表示PWM信号，其中载波和参考基频各自对应于一个独立变量。使用二重傅立叶级数分解二维函数，然后将其转换回涉及两个频率的时间函数，以给出一般性的PWM波形的频谱。

2.1 二维函数描述PWM

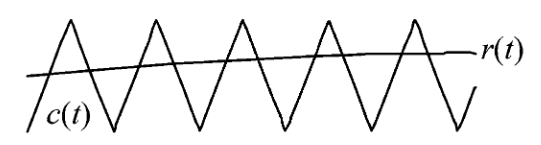
  通过堆叠多个载波和基准信号去表示PWM，如图a，b为后沿调制PWM信号表示形式，图c则表示通过堆叠多个载波和多个信号
{ c ( t ) , r ( t ) } , { C m + c ( t ) , C m + r ( t ) } , { 2 C m + c ( t ) , 2 C m + r ( t ) } . . . \{c(t),r(t)\},\{C_m+c(t),C_m+r(t)\},\{2C_m+c(t),2C_m+r(t)\}... {c(t),r(t)},{Cm​+c(t),Cm​+r(t)},{2Cm​+c(t),2Cm​+r(t)}...其中Cm是载波信号的峰峰振幅。线AB是原始锯齿信号的第一斜率的延伸，水平线 $l_0,l_1,l_2,...$ 将堆叠的载流分开，并且彼此间隔Cm。从对比图中可以明显的观察到线AB与堆叠信号的交点与传统PWM信号交点相同。c(t)与r(t)的交点便可描述PWM的波形变换，因此两种方式定义了相同的PWM波形。

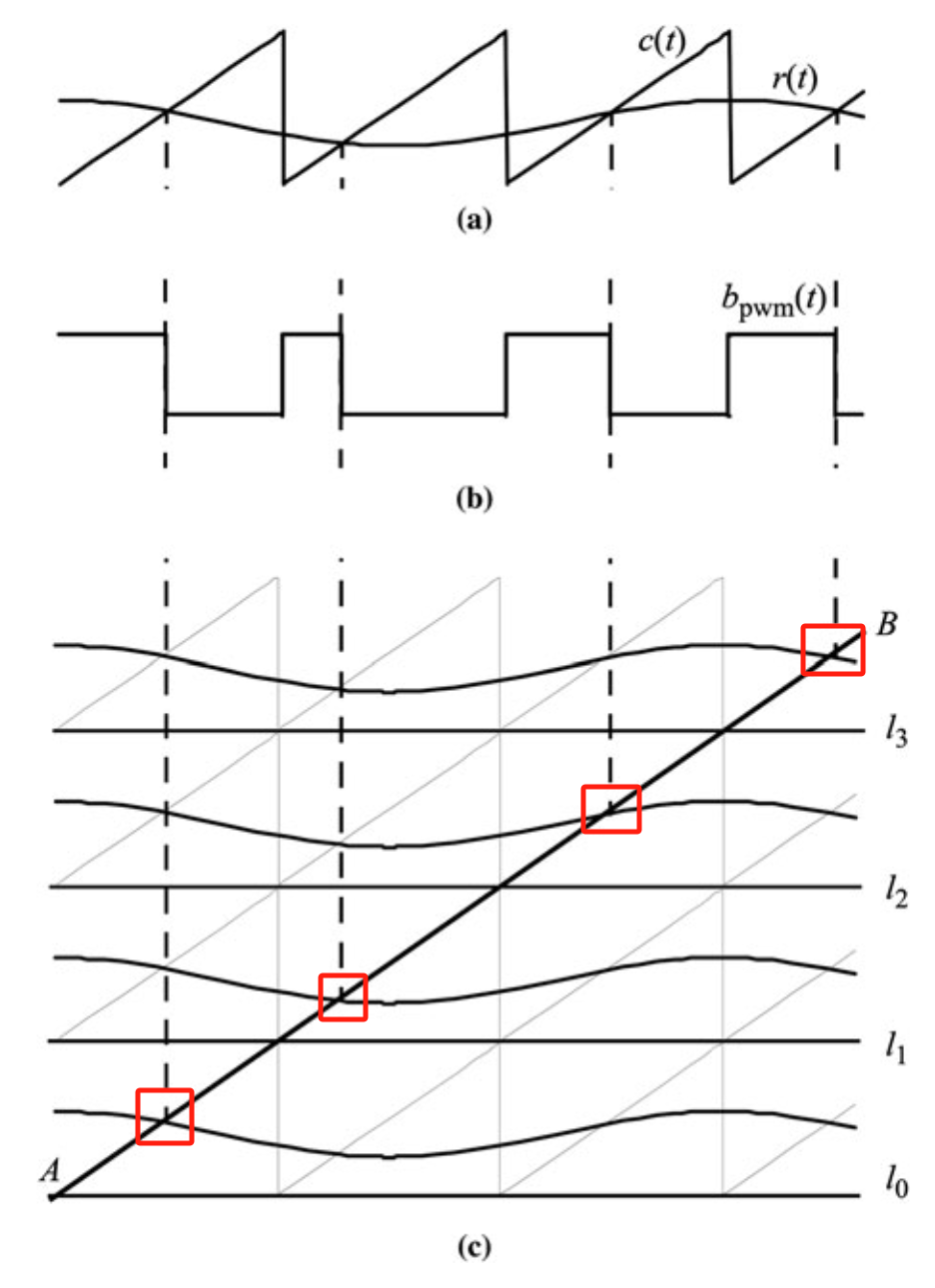
三角信号的PWM也可以用类似的方法表示，如图所示

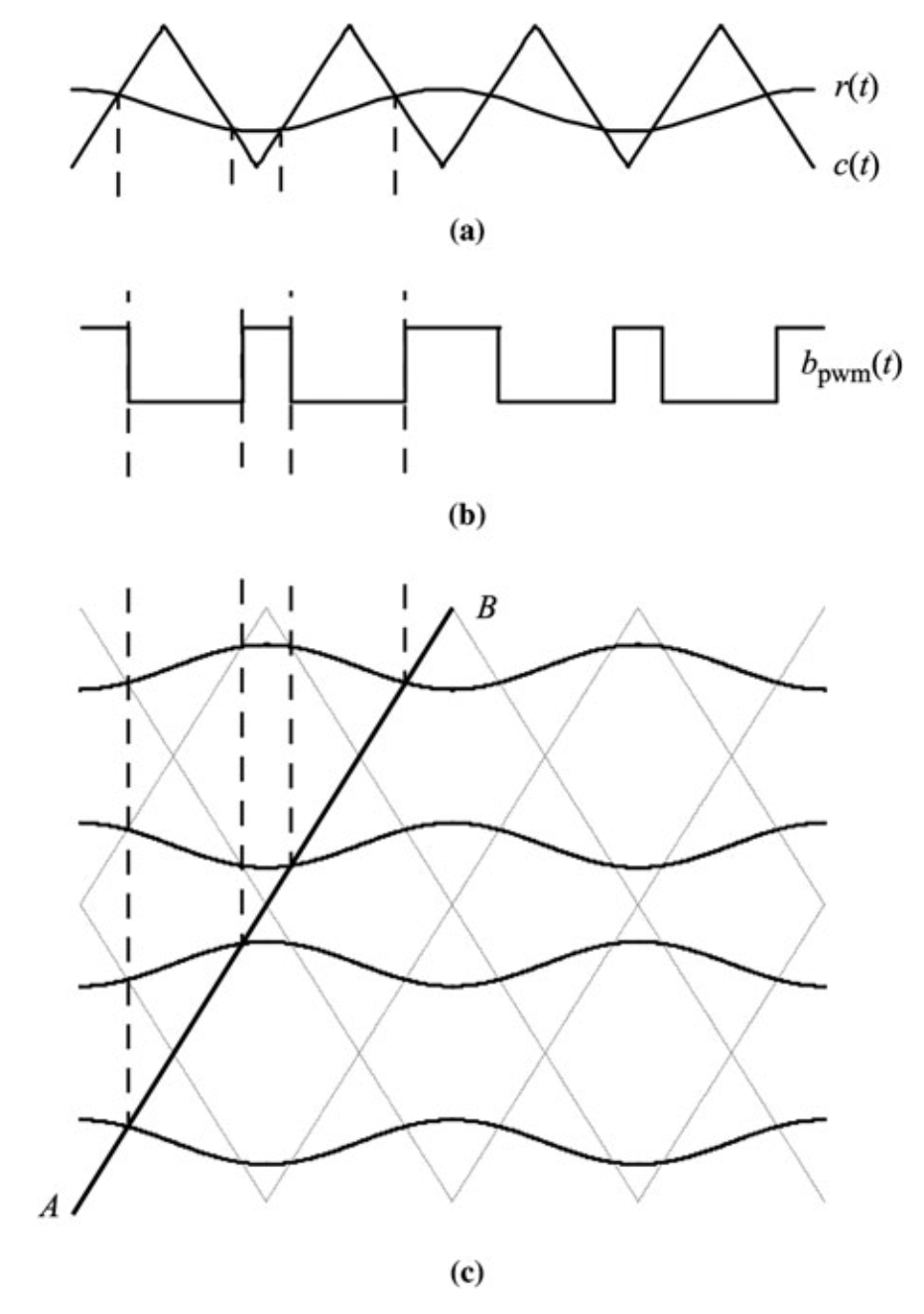
堆叠的载波：$$c（t）、2Cm-C（t）、2Cm+c（t）、4Cm-C（t）、...，$$堆叠的参考信号：$$r（t）、2Cm-R（t）、2Cm+r（t）、4Cm-R（t）、....$$线AB是原始载流子c(t)的第一个三角形的上升边的延伸。注意，线AB与堆叠参考的交点与原始载波和参考之间的交点相同。

根据上述描述可以定义一个二维函数表示PWM信号：
$$f(2\pi f_{1}t+{\theta }_1,2\pi f_{c}t+{\theta }_c)$$分别用 $x=2\pi f_{1}t+{\theta }_1$ 和 $y=2\pi f_{c}t+{\theta }_c$ 分别表示参考信号和载波的角频率，通过对该函数进行二重傅里叶变换获得PWM波形的频谱模型。通过该方法定义的PWM信号不需要明确PWM波形，载波和参考基频之间的关系也没有限制。下图是函数$z=f(x,y)$定义的三维图，当点$(x,y)$位于任何阴影区域内时，该函数等于+1，否则等于-1。

2.2 二重傅里叶级数（Double Fourier Series）

函数$f(x,y)$在x和y上都是周期性的，在两个轴上的周期等于$2\pi$，则可以用一个二重傅立叶级数表示，其形式为:
$$\begin{array}{rl}f(x,y)=& \frac{A_{00}}{2}+\sum _{n=1}^{+\infty }\left(A_{0n}\cos ny+B_{0n}\sin ny\right)+\sum _{m=1}^{+\infty }\left(A_{m0}\cos mx+B_{m0}\sin mx\right)\\ & +\sum _{m=1}^{+\infty }\sum _{n=\pm 1}^{\pm \infty }\left(A_{mn}\cos (mx+ny)+B_{mn}\sin (mx+ny)\right)\end{array}$$
参数定义如下
$$\begin{array}{rl}& A_{mn}=\frac{1}{2{\pi }^2}{\int }_0^{2\pi }{\int }_0^{2\pi }f(x,y)\cos (mx+ny)\mathrm{d}x\mathrm{d}y,\\ & B_{mn}=\frac{1}{2{\pi }^2}{\int }_0^{2\pi }{\int }_0^{2\pi }f(x,y)\sin (mx+ny)\mathrm{d}x\mathrm{d}y.\end{array}$$

三、PWM频谱模型

结合第二节给出的PWM二维函数形式，本节将给出常用恒频PWM方式的二重傅里叶模型。

说明

1. 单极调制：载波在0和正峰Cm之间变化，参考信号始终为正，PWM输出在0和1之间切换。
2. 双极调制：载波以零为对称，振幅等于Cm；参考信号是没有DC偏移的正弦波，PWM输出在-1/2和+1/2之间切换。
3. 定义平均占空比:
   $$D=\frac{R_0}{C_m}$$
4. 定义调制度:
   $$M=\frac{2R_1}{C_m}.$$
5. 每个频谱模型还包括定义如下的第一类贝塞尔函数, $J_n(z)$:

$$J_n(z)=\frac{{\mathrm{j}}^{-n}}{\pi }{\int }_0^{2\pi }{\mathrm{e}}^{\mathrm{j}z\cos \theta }{\mathrm{e}}^{\mathrm{j}n\theta }\mathrm{d}\theta .$$

频谱模型

1. 单极性后沿调制
   
   展开式：
   b p w m ( t ) = D + M 2 cos ⁡ ( ω 1 t + θ 1 ) + ∑ m = 1 + ∞ 1 m π { sin ⁡ [ m ( ω c t + θ c ) ] − J 0 ( m π M ) sin ⁡ [ m ( ω c t + θ c ) − 2 m D π ] } + ∑ m = 1 + ∞ ∑ n = ± 1 ± ∞ J n ( m π M ) m π × sin ⁡ [ n π 2 − m ( ω c t + θ c ) − n ( ω 1 t + θ 1 ) + 2 m D π ] . \begin{aligned} b_{\mathrm{pwm}}(t)= & D+\frac{M}{2} \cos \left(\omega_1 t+\theta_1\right) \\ & +\sum_{m=1}^{+\infty} \frac{1}{m \pi}\left\{\sin \left[m\left(\omega_c t+\theta_c\right)\right]\right. \\ & \left.-J_0(m \pi M) \sin \left[m\left(\omega_c t+\theta_c\right)-2 m D \pi\right]\right\} \\ & +\sum_{m=1}^{+\infty} \sum_{n= \pm 1}^{ \pm \infty} \frac{J_n(m \pi M)}{m \pi} \\ & \times \sin \left[\frac{n \pi}{2}-m\left(\omega_c t+\theta_c\right)-n\left(\omega_1 t+\theta_1\right)+2 m D \pi\right] . \end{aligned} bpwm​(t)=​D+2M​cos(ω1​t+θ1​)+m=1∑+∞​mπ1​{sin[m(ωc​t+θc​)]−J0​(mπM)sin[m(ωc​t+θc​)−2mDπ]}+m=1∑+∞​n=±1∑±∞​mπJn​(mπM)​×sin[2nπ​−m(ωc​t+θc​)−n(ω1​t+θ1​)+2mDπ].​
2. 双极性后沿调制，R0=0
   
   展开式：
   $$\begin{array}{rl}{b}_{\mathrm{pwm}}(t)=& \frac{M}{2}\cos \left({\omega }_{1}t+{\theta }_1\right)\\ & +\sum _{m=1}^{+\infty }\frac{1}{m\pi }\left[\cos (m\pi )-J_0(m\pi M)\right]\sin \left[m\left({\omega }_{c}t+{\theta }_c\right)\right]\\ & +\sum _{m=1}^{+\infty }\sum _{n=\pm 1}^{\pm \infty }\frac{J_n(m\pi M)}{m\pi }\sin \left[\frac{n\pi }{2}-m\left({\omega }_{c}t+{\theta }_c\right)-n\left({\omega }_{1}t+{\theta }_1\right)\right].\end{array}$$
3. 单极性前沿调制
   
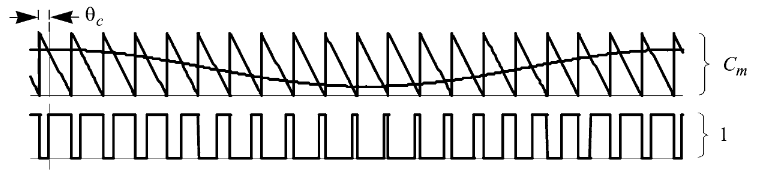
   展开式：
   b p w m ( t ) = D + M 2 cos ⁡ ( ω 1 t + θ 1 ) − ∑ m = 1 + ∞ 1 m π { sin ⁡ [ m ( ω c t + θ c ) ] − J 0 ( m π M ) sin ⁡ [ m ( ω c t + θ c ) + 2 m D π ] } − ∑ m = 1 + ∞ ∑ n = ± 1 ± ∞ J n ( m π M ) m π × sin ⁡ [ n π 2 − m ( ω c t + θ c ) − n ( ω 1 t + θ 1 + π ) − 2 m D π ] . \begin{aligned} b_{\mathrm{pwm}}(t)= & D+\frac{M}{2} \cos \left(\omega_1 t+\theta_1\right) \\ & -\sum_{m=1}^{+\infty} \frac{1}{m \pi}\left\{\sin \left[m\left(\omega_c t+\theta_c\right)\right]\right. \\ & \left.-J_0(m \pi M) \sin \left[m\left(\omega_c t+\theta_c\right)+2 m D \pi\right]\right\} \\ & -\sum_{m=1}^{+\infty} \sum_{n= \pm 1}^{ \pm \infty} \frac{J_n(m \pi M)}{m \pi} \\ & \times \sin \left[\frac{n \pi}{2}-m\left(\omega_c t+\theta_c\right)-n\left(\omega_1 t+\theta_1+\pi\right)-2 m D \pi\right] . \end{aligned} bpwm​(t)=​D+2M​cos(ω1​t+θ1​)−m=1∑+∞​mπ1​{sin[m(ωc​t+θc​)]−J0​(mπM)sin[m(ωc​t+θc​)+2mDπ]}−m=1∑+∞​n=±1∑±∞​mπJn​(mπM)​×sin[2nπ​−m(ωc​t+θc​)−n(ω1​t+θ1​+π)−2mDπ].​
4. 双极性前沿调制，R0=0
   
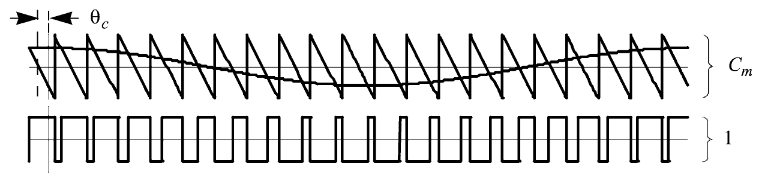
   展开式：
   $$\begin{array}{rl}{b}_{\mathrm{pwm}}(t)=& \frac{M}{2}\cos \left({\omega }_{1}t+{\theta }_1\right)\\ & -\sum _{m=1}^{+\infty }\frac{1}{m\pi }\left[\cos (m\pi )-J_0(m\pi M)\right]\sin \left[m\left({\omega }_{c}t+{\theta }_c\right)\right]\\ & -\sum _{m=1}^{+\infty }\sum _{n=\pm 1}^{\pm \infty }\frac{J_n(m\pi M)}{m\pi }\\ & \times \sin \left[\frac{n\pi }{2}-m\left({\omega }_{c}t+{\theta }_c\right)-n\left({\omega }_{1}t+{\theta }_1+\pi \right)\right].\end{array}$$
5. 单极性双边沿调制
   
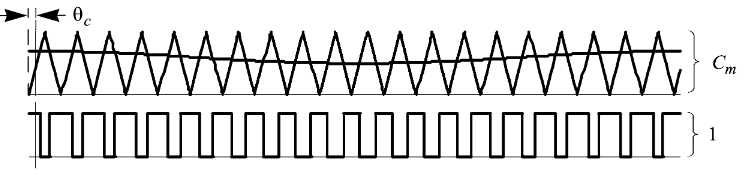
   展开式：
   $$\begin{array}{rl}{b}_{\mathrm{pwm}}(t)=& D+\frac{M}{2}\cos \left({\omega }_{1}t+{\theta }_1\right)\\ & +\sum _{m=1}^{+\infty }\frac{2}{m\pi }{J}_0\left(\frac{m\pi M}{2}\right)\sin (Dm\pi )\cos \left[m\left({\omega }_{c}t+{\theta }_c\right)\right]\\ & +\sum _{m=1}^{+\infty }\sum _{n=\pm 1}^{\pm \infty }\frac{2}{m\pi }{J}_n\left(\frac{m\pi M}{2}\right)\sin \frac{(2Dm+n)\pi }{2}\\ & \times \cos \left[m\left({\omega }_{c}t+{\theta }_c\right)+n\left({\omega }_{1}t+{\theta }_1\right)\right].\end{array}$$
6. 双极性双边沿调制，R0=0
   
   展开式：
   $$\begin{array}{rl}{b}_{\mathrm{pwm}}(t)=& \frac{M}{2}\cos \left({\omega }_{1}t+{\theta }_1\right)\\ & +\sum _{m=1}^{+\infty }\frac{2}{m\pi }{J}_0\left(\frac{m\pi M}{2}\right)\sin \frac{m\pi }{2}\cos \left[m\left({\omega }_{c}t+{\theta }_c\right)\right]\\ & +\sum _{m=1}^{+\infty }\sum _{n=\pm 1}^{\pm \infty }\frac{2}{m\pi }{J}_n\left(\frac{m\pi M}{2}\right)\sin \frac{(m+n)\pi }{2}\\ & \times \cos \left[m\left({\omega }_{c}t+{\theta }_c\right)+n\left({\omega }_{1}t+{\theta }_1\right)\right]\end{array}$$

四、总结

  本文介绍的PWM频谱模型适用于大多数的PWM应用场景，参考文献的后续章节还有各种不同调制方式下的小信号模型介绍但与我本人课题研究的关联性较低，我并未详细阅读有需要的同学请自行下载阅读。

这篇关于文献阅读--Pulse-Width Modulation的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---