本文主要是介绍基于二分图匹配算法的商家保量系统实践,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、背景
商家扶持保量系统的业务功能,是保证重点签约商家能够在当天拿到预期的流量。比较简单的保量方案是通过pid算法控制,即根据每个商家的放量进度输出pid系数(比如值域[1, 16]),乘以pxtr排序公式后参与最终排序,pid系数越高排序靠前的概率更高,该排序算法弊端是:
- 仅考虑商家的流量缺口,缺口越大透出概率越大,pxtr作用较小,流量匹配效率低下
- 商家给量不均匀,可能在商家直播的某个时间段给过高流量,导致商家效率不足
本文重点介绍的二分图匹配算法能够做到在匹配窗口内的流量分配全局最优,兼顾流量的分发效率和商家的流量需求,预期大幅提升扶持流量的整体效率,从而带动推荐系统整体效率提升。
二、匹配算法介绍
1、定义凸优化问题
min − ∑ i , j w i , j V j x i , j + λ 2 ∑ i , j ∥ x i , j − p j ∥ 2 s . t . ∑ j x i , j ≤ 1 , ∀ i ( 1 ) ∑ i x i , j ≥ d j , ∀ i ( 2 ) x i , j ≥ 0 , ∀ i , j ( 3 ) \min{-\sum_{i,j}w_{i,j}V_j x_{i,j}} + \frac{\lambda}{2} \sum_{i,j}\|x_{i,j} - p_j\|^2\\ \begin{aligned} s.t. \quad \sum_j x_{i,j} & \le 1,\quad \forall i &(1)\\ \sum_i x_{i,j} & \ge d_j,\quad \forall i & (2)\\ x_{i,j} & \ge0,\quad \forall i,j & (3) \end{aligned} min−i,j∑wi,jVjxi,j+2λi,j∑∥xi,j−pj∥2s.t.j∑xi,ji∑xi,jxi,j≤1,∀i≥dj,∀i≥0,∀i,j(1)(2)(3)
其中:
i , j i,j i,j:表示第i次请求和第j个商家
w i , j w_{i,j} wi,j:表示第i次请求中用户对第j个商家的价值贡献,一般为pxtr的公式组合
V j V_j Vj:表示第j个商家的高光系数,亦即该商家的优先级
x i , j x_{i,j} xi,j:表示第i次请求透出第j个商家的概率,为待求解变量
d j d_j dj:表示第j个商家提报流量
p j = d j ∑ j d j p_{j} = \frac{d_j}{\sum_j d_j} pj=∑jdjdj:表示第j个商家平均能分配流量的比例,可以控制流量分配的平滑程度
注意:约束条件中
第一个为一次请求中只能选择最多给一个商家透出
第二个为对一个商家的累计曝光需要超过提报量
第三个为透出概率大于0
2、参数推导
凸优化问题转化为拉格朗日对偶问题
min − ∑ i , j w i , j V j x i , j + λ 2 ∑ i , j ∥ x i , j − p j ∥ 2 + ∑ i β i ( ∑ j x i , j − 1 ) − ∑ j α j ( ∑ i x i , j − d j ) − ∑ i , j γ i , j x i , j \min{-\sum_{i,j}w_{i,j}V_j x_{i,j}} + \frac{\lambda}{2} \sum_{i,j}\|x_{i,j} - p_j\|^2 + \sum_{i}\beta_i \big(\sum_{j}x_{i,j} - 1\big) - \sum_{j}\alpha_j \big(\sum_{i}x_{i,j} - d_j\big) - \sum_{i,j}\gamma_{i,j}x_{i,j} min−i,j∑wi,jVjxi,j+2λi,j∑∥xi,j−pj∥2+i∑βi(j∑xi,j−1)−j∑αj(i∑xi,j−dj)−i,j∑γi,jxi,j
求导等于0得到
x i , j = ( α j − β i + w i , j V j + γ i , j ) / λ + p j x_{i,j} = (\alpha_j-\beta_i+w_{i,j}V_j + \gamma_{i,j})/\lambda + p_j xi,j=(αj−βi+wi,jVj+γi,j)/λ+pj
根据KKT条件,要么 γ i , j = 0 \gamma_{i,j} = 0 γi,j=0,要么 x i , j = 0 x_{i,j} = 0 xi,j=0,因此上式可以简化为
x i , j = max ( 0 , α j − β i + w i , j V j λ + p j ) = g i , j ( α j − β i ) \begin{aligned} x_{i,j} &= \max(0, \frac{\alpha_j-\beta_i+w_{i,j}V_j}{\lambda} + p_j) \\ &= g_{i,j}(\alpha_j - \beta_i) \end{aligned} xi,j=max(0,λαj−βi+wi,jVj+pj)=gi,j(αj−βi)
3、离线求解
不用考虑剩余流量(因为本方案没有人群限制,即对所有用户生效),利用坐标梯度下降法求解 α j \alpha_j αj和 β i \beta_i βi
1、对所有 j j j,初始化 α j = 0 \alpha_j = 0 αj=0
2、对于所有的流量 i i i,假设 α j \alpha_j αj已知,计算 β i \beta_i βi,使之满足
∑ j x i , j = 1 \sum_j x_{i,j} = 1 j∑xi,j=1
代入表达式即
∑ j g i , j ( α j − β i ) = 1 \sum_j g_{i,j}(\alpha_j - \beta_i) = 1 j∑gi,j(αj−βi)=1
否则 β i \beta_i βi无解,设置为0
3、对于所有的商家 j j j,假设 β i \beta_i βi已知,计算 α j \alpha_j αj,使之满足
∑ i x i , j = d j \sum_i x_{i,j} = d_j i∑xi,j=dj
代入表达式即
∑ i g i , j ( α j − β i ) = d j \sum_i g_{i,j}(\alpha_j - \beta_i) = d_j i∑gi,j(αj−βi)=dj
否则 α j \alpha_j αj无解,设置为0
4、重复上述2、3步骤,直到 α j \alpha_j αj和 β i \beta_i βi收敛(实际限制最多迭代轮数即可)
注:在线存储只保存 α j \alpha_j αj
4、在线匹配
1、对于所有的流量 i i i,利用离线计算的 α j \alpha_j αj计算 β i \beta_i βi,使之满足
∑ j x i , j = 1 \sum_j x_{i,j} = 1 j∑xi,j=1
代入表达式即
∑ j g i , j ( α j − β i ) = 1 \sum_j g_{i,j}(\alpha_j - \beta_i) = 1 j∑gi,j(αj−βi)=1
否则 β i \beta_i βi无解,设置为0
2、利用 α j \alpha_j αj和 β i \beta_i βi计算
x i , j = g i , j ( α j − β i ) = max ( 0 , ( α j − β i + w i , j V j ) / λ + p j ) \begin{aligned} x_{i,j} &= g_{i,j}(\alpha_j - \beta_i) \\ &=\max(0, (\alpha_j-\beta_i+w_{i,j}V_j)/\lambda + p_j) \end{aligned} xi,j=gi,j(αj−βi)=max(0,(αj−βi+wi,jVj)/λ+pj)
并使用 x i , j x_{i,j} xi,j作为商家透出的概率,降序排列截取top
三、保量系统功能实践
系统分为三个主要模块
1、实时更新服务:获取商家实时获取曝光量,从而计算出该商家缺口曝光量,用来更新流量额度d和分配比例p
2、离线参数求解服务:记录每次请求模型预估组合打分 w i , j w_{i,j} wi,j,在线累计10w次请求后执行离线求解过程得到 α j \alpha_j αj和 β i \beta_i βi,最终只保存 α j \alpha_j αj
3、在线计算服务:处理实时请求时,使用离线求解的 α j \alpha_j αj和传入的 w i , j w_{i,j} wi,j根据公式计算得到 β i \beta_i βi,再根据公式计算得到 x i , j x_{i,j} xi,j作为商家透出的概率,降序排列截取top
整体流程如下:
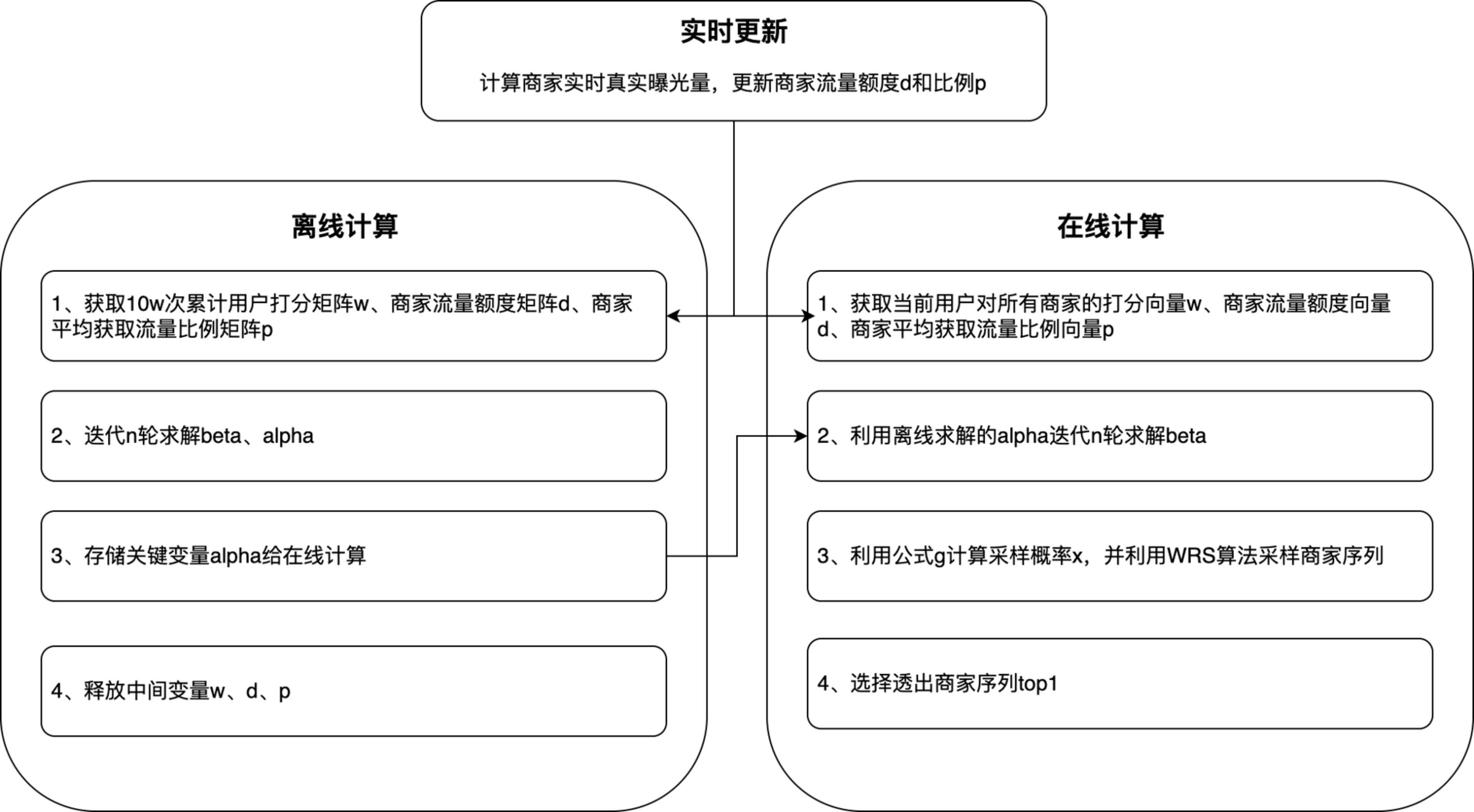
1、离线求解代码实现
根据第二节的第3步可以看到,求解的公式都是带有max操作的一次方程,参考Solve equations using the max
function,可以转化为分段闭式解求解。迭代循环代码如下
for (int iter = 1; iter <= 20; ++iter) {LOG(INFO) << "begin iter=" << iter;// update betafor (int i = 0; i < user_num; ++i) {betas[i] = SolveBeta(alphas, user_flow_[i], probabilities, photo_num);}// update alphafor (int j = 0; j < photo_num; ++j) {alphas[j] = SolveAlpha(betas, photo_flow_[j], photo_allocation_[j], probabilities[j], demands[j], user_num);}// ensure non-negative alpha and betaint64_t min_alpha_beta = INT64_MAX;for (int i = 0; i < user_num; ++i) {min_alpha_beta = std::min(betas[i], min_alpha_beta);}for (int j = 0; j < photo_num; ++j) {min_alpha_beta = std::min(alphas[j], min_alpha_beta);}// alpha beta >= 0 ensure min_alpha_beta >= 0for (int i = 0; i < user_num; ++i) {betas[i] -= min_alpha_beta;}for (int j = 0; j < photo_num; ++j) {alphas[j] -= min_alpha_beta;}
}
求解 b e t a beta beta和 a l p h a alpha alpha的代码如下
float SolveBeta(const float *alphas, const float *weights, float *probabilities, size_t photo_num) {std::vector<float> target;for (size_t j = 0; j < photo_num; ++j) {if (probabilities[j] <= 0 || weights[j] <= 0) { // user_flow_矩阵稀疏求解continue;}float alpha_score = alphas[j] + weights[j] + OBJECT_LAMBDA * probabilities[j];target.push_back(alpha_score);}float beta = 0.0;std::sort(target.begin(), target.end(), std::greater<float>());float target_sum = 0.0;float coef_sum = 0.0;int64_t solve_success = 0;for (size_t j = 0; j < target.size(); ++j) {target_sum += target[j];coef_sum += 1.0;float tmp_beta = (target_sum - OBJECT_LAMBDA) / coef_sum;if (tmp_beta > 0 && tmp_beta <= target[j]){beta = tmp_beta;solve_success = 1;break;}}return beta;
}float SolveAlpha(const float *betas, const float *weights, float probability, float demand, size_t user_num) {if (probability <= 0 || demand <= 0) { // photo_flow_矩阵稀疏求解return 0;}std::vector<float> target;for (size_t i = 0; i < user_num; ++i) {if (weights[i] <= 0) { // user_flow_矩阵稀疏求解continue;}float beta_score = weights[i] - betas[i] + OBJECT_LAMBDA * probability;target.push_back(beta_score);}float alpha = 0.0;std::sort(target.begin(), target.end(), std::greater<float>());float target_sum = 0.0;float coef_sum = 0.0;int64_t solve_success = 0;for (size_t i = 0; i < target.size(); ++i) {target_sum += target[i];coef_sum += 1.0;float tmp_alpha = (OBJECT_LAMBDA * demand / MAX_SCORE - target_sum) / coef_sum;if (tmp_alpha > 0 && tmp_alpha >= -target[i]){alpha = tmp_alpha;solve_success = 1;break;}}return alpha;
}
2、在线求解代码实现
在线求解只需要根据保存的 α \alpha α求解 β \beta β即可,流程和离线求解一致
float OnlineSolveBeta(const float *alphas, const float *weights, float *probabilities, size_t candidate_size) {std::vector<float> target;for (size_t j = 0; j < candidate_size; ++j) {if (probabilities[j] <= 0 || weights[j] <= 0) { // user_flow_矩阵稀疏求解continue;}float alpha_score = alphas[j] + weights[j] + OBJECT_LAMBDA * probabilities[j];target.push_back(alpha_score);}float beta = 0.0;std::sort(target.begin(), target.end(), std::greater<float>());float target_sum = 0.0;float coef_sum = 0.0;int64_t solve_success = 0;for (size_t j = 0; j < target.size(); ++j) {target_sum += target[j];coef_sum += 1.0;float tmp_beta = (target_sum - OBJECT_LAMBDA) / coef_sum;if (tmp_beta > 0 && tmp_beta <= target[j]){beta = tmp_beta;solve_success = 1;break;}}return beta;
}
四、参考
https://segmentfault.com/a/1190000021419023
https://mp.weixin.qq.com/s/2VejGdsZrCxB8pD1y7Bqhg
https://zhuanlan.zhihu.com/p/348022042
https://zhuanlan.zhihu.com/p/123187987
https://zhuanlan.zhihu.com/p/36051733
https://github.com/wangrunjie/SHALE/tree/94b47ccbe4b4cabe233c9512350969cda57f2e08
https://math.stackexchange.com/questions/145458/solve-equations-using-the-max-function
这篇关于基于二分图匹配算法的商家保量系统实践的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






