本文主要是介绍写给学生看的系统分析与验证笔记(十一)——Generalized NBA(GNBA),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
- Generalized NBA
- GNBA转NBA
在上一节中我们介绍了非确定的Büchi automata,这节中我们介绍一下Generalized NBA,即广义的非确定性NBA。
Generalized NBA
GNBA也是由一个五元组 G = ( Q , Σ , q 0 , F , δ ) \mathcal{G}=(Q,Σ,q_{0},\mathcal{F},δ) G=(Q,Σ,q0,F,δ)构成,其中 Q , Σ , q 0 . δ Q,Σ,q_{0}.δ Q,Σ,q0.δ含义都与NBA中的一样,但是F表示为接受状态集合的集合(set of accept sets),表示为 F ⊆ 2 Q \mathcal{F}\subseteq 2^Q F⊆2Q, F \mathcal{F} F可以是类似 { F 1 , F 2 , . . . , F k } \{F_{1},F_{2},...,F_{k}\} {F1,F2,...,Fk}的形式。
对GNBA来说,如果一个运行 q 0 q 1 q 2 . . . q_{0}q_{1}q_{2}... q0q1q2...是可接受的,那么表示,每个接受状态集合将会被无限经常次访问。
直白说,NBA的F是一个集合,它要求运行可以无限经常次访问接受状态集合里面的元素,而GBNA的 F \mathcal{F} F是一个集合的集合,它要求运行可以无限经常次访问集合里面的每一个集合中的元素,这么看来GNBA的确是一种广义的NBA,当GNBA的F中只有一个集合的时候,就变成了NBA。
用符号表示为:
∀ F ∈ F ∃ ∞ i ∈ N s . t . q i ∈ F \forall F∈\mathcal{F}\text{ }\overset{∞}\exist\text{ }i∈N s.t. q_{i}∈F ∀F∈F ∃∞ i∈Ns.t.qi∈F
GNBA可接受的语言表示为:
L ω ( G ) = { σ ∈ Σ ω ∣ 无 限 字 σ 输 入 自 动 机 存 在 一 条 可 接 受 的 运 行 } L_{\omega}(\mathcal{G})=\{\sigma∈Σ^\omega|无限字\sigma输入自动机存在一条可接受的运行\} Lω(G)={σ∈Σω∣无限字σ输入自动机存在一条可接受的运行}
用GNBA表示活性(liveness)
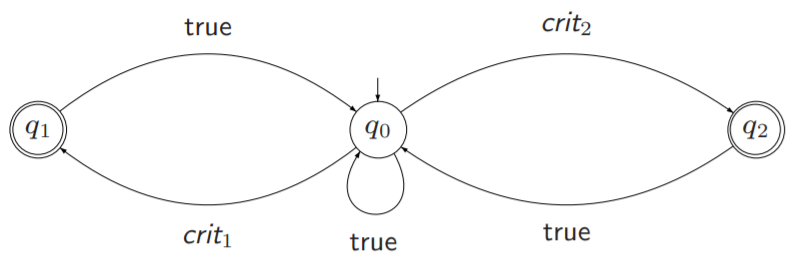
两个进程无限经常次进入临界区,这个LT属性可以用GNBA表示,此时的 F = { { q 1 } , { q 2 } } \mathcal{F}=\{\{q_{1}\},\{q_{2}\}\} F={{q1},{q2}}
GNBA转NBA
首先我们要知道,对于每一个GNBA来说,存在一个NBA使得
L ω ( G ) = L ω ( A ) L_{\omega}(\mathcal{G})=L_{\omega}(\mathcal{A}) Lω(G)=Lω(A)
F = { F 1 , F 2 , . . . , F k } \mathcal{F}=\{F_{1},F_{2},...,F_{k}\} F={F1,F2,...,Fk},当k=1时,它就是一个NBA,而当k>1时

从初始状态 Q 0 Q_{0} Q0出发,我们可以将 { F 1 , F 2 , . . . , F k } \{F_{1},F_{2},...,F_{k}\} {F1,F2,...,Fk}分成k个GNBA的拷贝,要注意的是,只有在某个拷贝中访问了接受集合 F k F_{k} Fk后才能访问下一个拷贝,这样依次下去,直到几个拷贝连成环,这样就生成了一个NBA
接下里讲述具体的算法:
假设 G = ( Q , Σ , Q 0 , F , δ ) \mathcal{G}=(Q,Σ,Q_{0},\mathcal{F},δ) G=(Q,Σ,Q0,F,δ)是一个GNBA, A = ( Q ′ , Σ , Q 0 ′ , F ′ , δ ′ ) A=(Q',Σ,Q'_{0},F',δ') A=(Q′,Σ,Q0′,F′,δ′)是一个NBA,为了顺利转换,我们需要在状态上增添常数i,用它表示某个状态属于第i个部分
- Q ′ = Q × { 1 , 2 , . . . k } Q'=Q×\{1,2,...k\} Q′=Q×{1,2,...k}
- Q 0 ′ = Q 0 × { 1 } = { < q 0 , 1 > ∣ q 0 ∈ Q 0 } Q'_{0}=Q_{0}×\{1\}=\{<q_{0},1> |q_{0}∈Q_{0}\} Q0′=Q0×{1}={<q0,1>∣q0∈Q0}
- F 1 ′ = F 1 × { 1 } = { < q 0 , 1 > ∣ q F ∈ F 1 } F'_{1}=F_{1}×\{1\}=\{<q_{0},1> |q_{F}∈F_{1}\} F1′=F1×{1}={<q0,1>∣qF∈F1}
- δ ′ ( < q , i > , a ) = { { q ′ . i } ∣ q ′ ∈ δ ( q , a ) i f q ∉ F i { q ′ . i + 1 } ∣ q ′ ∈ δ ( q , a ) o t h e r w i s e δ'(<q,i>,a)=\begin{cases}\{q'.i\}|q'∈δ(q,a)\text{ }if\text{ }q\notin F_{i}\\ \{q'.i+1\}|q'∈δ(q,a)\text{ }otherwise \end{cases} δ′(<q,i>,a)={{q′.i}∣q′∈δ(q,a) if q∈/Fi{q′.i+1}∣q′∈δ(q,a) otherwise
大致公式就如上面所示, Q 0 Q_{0} Q0和 F 1 F_{1} F1都标记为第一个部分,发生转换时,如果当前状态不属于 F i F_{i} Fi,则下一个状态的标记i不变,如果当前是 F i F_{i} Fi中的状态发生了转换,那么下一个标记需要加1(其实这个公式还少了一部分,如果处于最后一个标记的的F,那么下一个标记应该仍未1)
下面是一个转换的例子

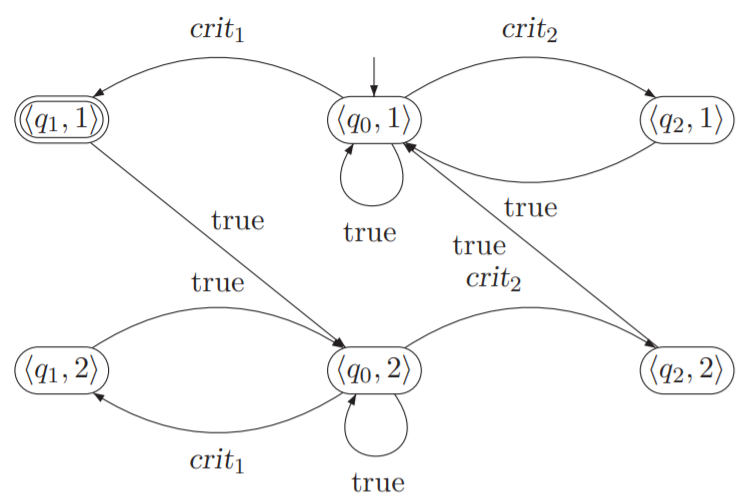
我们看到这副图,还是很清楚的,上下两个部分就相当于两个拷贝,在访问了接受状态F后,就会访问下一个拷贝,最后两个拷贝连起来形成一个环。
这篇关于写给学生看的系统分析与验证笔记(十一)——Generalized NBA(GNBA)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






