本文主要是介绍P9 中序遍历树并判断是否为二叉搜索树 (15 分),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
对给定的有N个节点(N>=0)的二叉树,给出中序遍历序列,并判断是否为二叉搜索树。
题目保证二叉树不超过200个节点,节点数值在整型int范围内且各不相同。
输入格式:
第一行是一个非负整数N,表示有N个节点
第二行是一个整数k,是树根的元素值
接下来有N-1行,每行是一个新节点,格式为r d e 三个整数,
r表示该节点的父节点元素值(保证父节点存在);d是方向,0表示该节点为父节点的左儿子,1表示右儿子;e是该节点的元素值
输出格式:
首先输出二叉树的中序遍历序列,每个元素占一行。对于空树,不输出任何内容。
然后如果给定的树是二叉搜索树,输出Yes 否则输出No
输入样例:
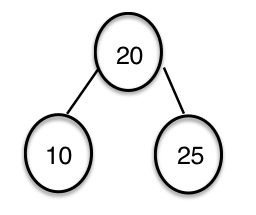
对于图片中的二叉树:
3
20
20 0 10
20 1 25
输出样例:
10
20
25
Yes
题解
最开始我试图用数组的方式来存二叉树,但是中序遍历的时候出现了问题。
后来还是改成了指针的形式
#include <iostream>
#include <cstdio>
#include <unordered_map>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> res, tmp;
int n;
const int N = 5000;
int arr[N];
struct tree{int val;tree* left;tree* right;tree(int x){val = x;left = right = nullptr;}
};
void inorder(tree* root){if(!root) return;inorder(root->left);cout<<root->val<<endl;res.push_back(root->val);inorder(root->right);
}
int main(){unordered_map<int, tree*> mp;cin>>n;int x, d, e;tree* root = nullptr;for(int i = 1; i <= n; i ++){cin>>x;if(i != 1){cin>>d>>e;auto r = mp[x];tmp.push_back(e);if(d == 0) { //左儿子 r->left = new tree(e);mp[e] = r->left;}else{ //右儿子 r->right = new tree(e);mp[e] = r->right;}}else{root = new tree(x);mp[x] = root;tmp.push_back(x);}}inorder(root); sort(tmp.begin(), tmp.end());if(res == tmp) cout<<"Yes"<<endl;else cout<<"No"<<endl;return 0;
}
这篇关于P9 中序遍历树并判断是否为二叉搜索树 (15 分)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



