本文主要是介绍正弦波生成的傅里叶级数展开法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录:
一、积分法
二、傅里叶级数展开法
附录、常见波形的傅里叶级数
一、积分法
通过对三角波进行积分,即可得到正弦波。有关内容移步:运算放大器应用汇总1之六、积分电路。
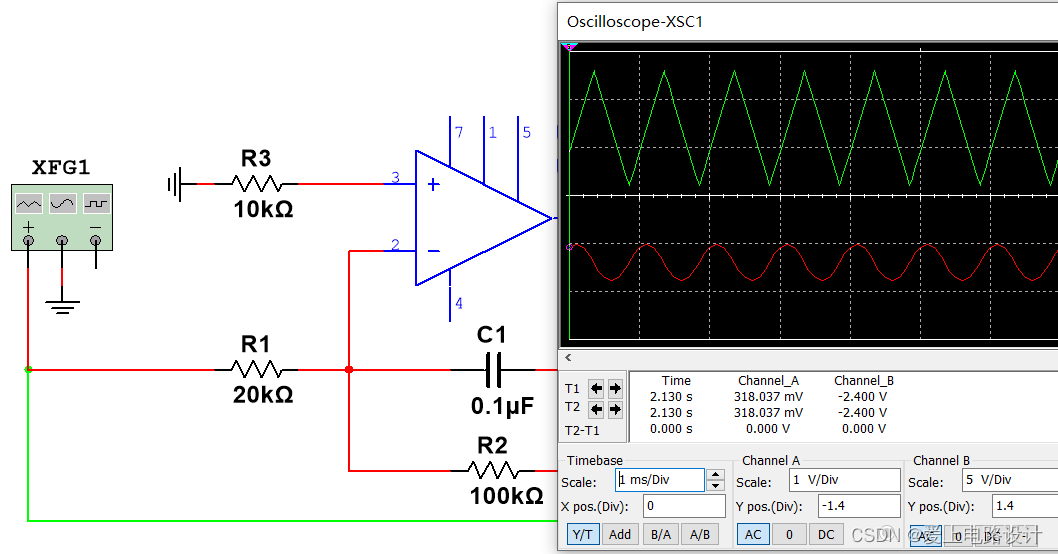
下面对傅里叶级数展开法进行描述。
二、傅里叶级数展开法
三角波可以看作是许多不同频率正弦波的叠加,有关内容移步:信号与系统。

通过对三角波进行傅里叶级数展开,可以得到基波和奇次谐波,如下图所示。该三角波在区间[-T/2,T/2]的傅里叶级数展开式为:
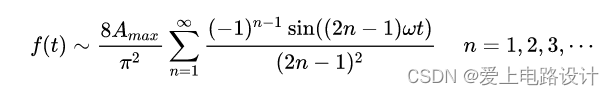
将其展开:
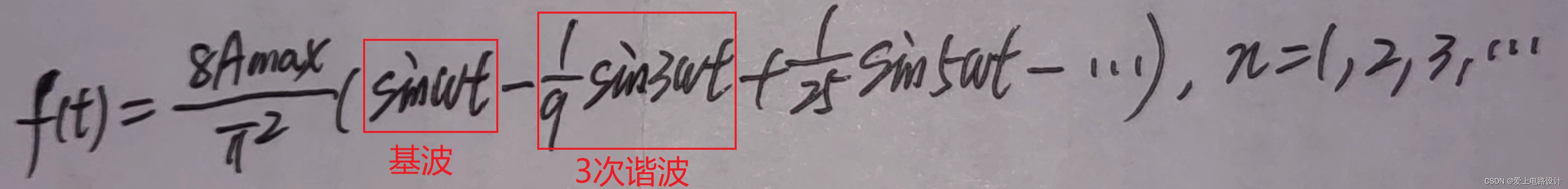
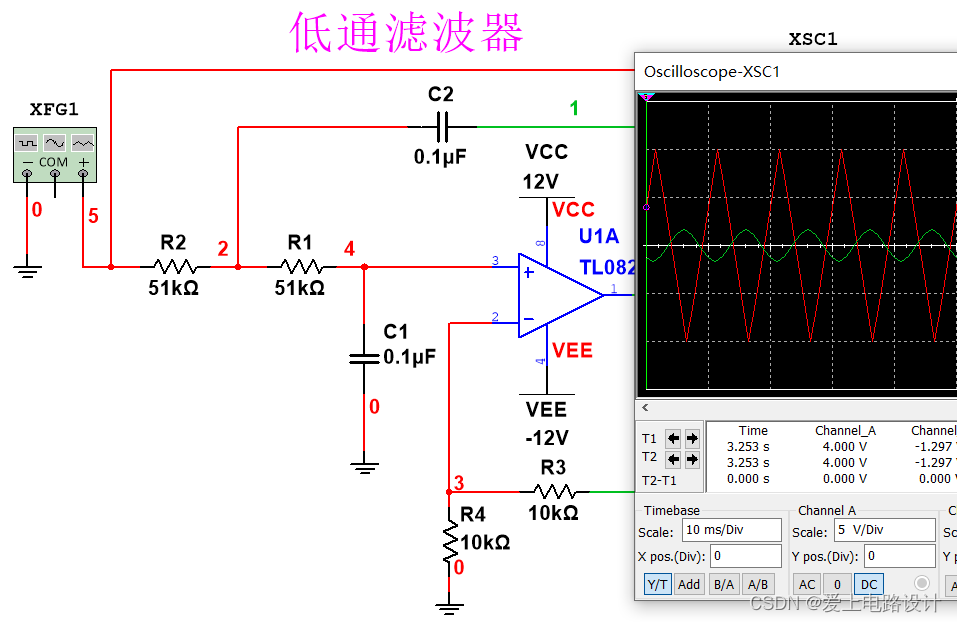
通过设计适当的低通滤波器,取出基波并滤除高次谐波,即可得到正弦波。
下面的电路为二阶低通滤波器:
原文件下载:三角波转正弦波
需要注意的是:此低通滤波器的通带截止频率应大于三角波的基波频率且小于三角波的三次谐波频率。
附录、常见波形的傅里叶级数
1、预备知识
1)公式
给定一个周期为的函数,那么它可以表示为无穷级数:
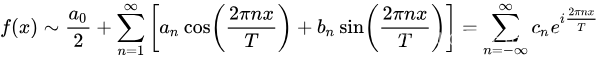
其中傅里叶系数为:

2)性质
- 收敛性
在闭区间上满足狄利克雷条件的函数表示成的傅里叶级数都收敛。狄利克雷条件如下:
- 在定义区间上,X(t)需绝对可积;
- 在任一有限区间中,X(t)只能取有限个极值点;
- 在任何有限区间上,X(t)只能有有限个第一类间断点。
满足上述条件的X(t)傅里叶级数都收敛,且:
- 当t是X(t)的连续点时,级数收敛于X(t)
- 当X(t)是X(t)的间断点时,级数收敛于
- 正交性
所谓的两个不同向量正交是指它们的内积为0,这也就意味着这两个向量之间没有任何相关性,例如,在三维欧式空间中,互相垂直的向量之间是正交的。三角函数族的正交性用公式表示出来就是:

- 奇偶性
奇函数fo(X)可以表示为正弦级数,而偶函数fe(X)则可以表示成余弦级数:

2、几种常见波形的傅里叶级数

如上图所示,该梯形波是一个周期为T的奇函数,幅值为Amax,上升沿时间为d,在区间[0,T/2]的函数表达式为:

由奇偶性可知,该波形在区间[-T/2,T/2]的傅里叶级数展开式为:

其中傅里叶系数为:

将f(t)函数代入傅里叶系数表达式中,可得:

由

可得:

综上所述,可以得到该梯形波在区间[-T/2,T/2]的傅里叶级数展开式为:
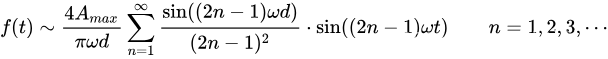
其中:ω = 2π/T。
1)脉冲波(偶函数)

如上图所示,该脉冲波是一个周期为T的偶函数,幅值为Amax,脉冲宽度为αT,在区间[-T/2,T/2]的函数表达式为:
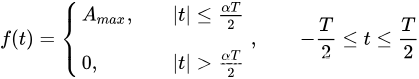
由奇偶性可知,该波形在区间[-T/2,T/2]的傅里叶级数展开式为:
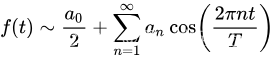
其中傅里叶系数为:
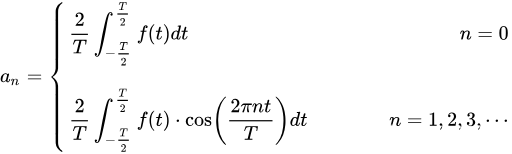
将f(t)函数代入傅里叶系数表达式中,可得:

因此,可以得到该梯形波在区间[-T/2,T/2]的傅里叶级数展开式为:
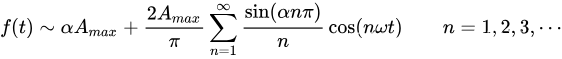
其中:ω = 2π/T。
2)方波(奇函数)
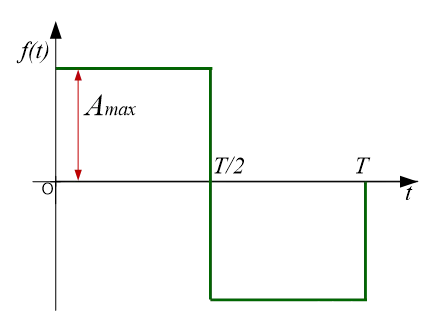
同理,该方波在区间[-T/2,T/2]的傅里叶级数展开式为:
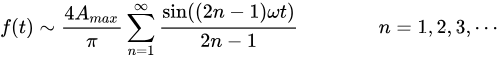
其中:ω = 2π/T。
3)三角波(奇函数)
上面已经有述,故不再赘述。
4)锯齿波(非奇非偶函数)

该锯齿波如上图所示,在区间[0,T]的函数表达式为:
![]()
由于该函数为非奇非偶函数,因此,该波形在区间[0,T]的傅里叶级数展开式为:
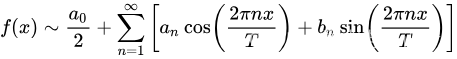
其中傅里叶系数为:
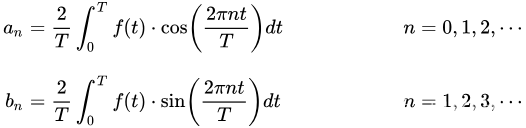
将f(t)函数代入傅里叶系数表达式中,可得:

因此,可以得到该锯齿波在区间[0,T]的傅里叶级数展开式为:
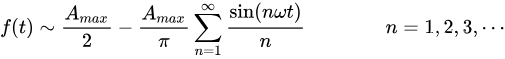
知道自己是什么年纪,并把这个年纪能做好的事情尽力做好,才可能有下个年纪的随心所欲。觉得不错,动动发财的小手点个赞哦!
这篇关于正弦波生成的傅里叶级数展开法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




