Leetcoder Day36｜ 动态规划part03

本文主要是介绍Leetcoder Day36｜ 动态规划part03，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

343. 整数拆分

给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。

示例 1:

• 输入: 2
• 输出: 1
• 解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:

• 输入: 10
• 输出: 36
• 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
• 说明: 你可以假设 n 不小于 2 且不大于 58。

本题需要注意的是，至少拆成2个正整数的和，而不是正好是2个正整数。

1. 确定dp数组以及下标的含义：dp[i]为整数i拆分后的最大乘积
2. 确定递推公式：假如将i拆分为j和i-j，这里j不只是代表一个数字而是一可能由j个整数组成的乘积。如果从1遍历到j，有两种途径可以得到dp[i]，一个是dp[i]=j*(i-j)，另一个是dp[i]=j*dp[i-j]，这里dp[i-j]代表i-j这个数字被拆分后的最大值。
3. dp数组如何初始化：本题将i拆成0是没有意义的，所以不考虑，1拆开只能是1和0，也是没有意义的，所以从2开始初始化，2可以拆成1 + 1，因此dp[2]=1
4. 确定遍历顺序：既然初始化是从2开始的，所以i从3开始遍历，j从1开始遍历，到i停止。
5. 举例推导dp数组：没法通过简单计算举例。

class Solution {public int integerBreak(int n) {int[] dp=new int[n+1]; dp[2]=1;for(int i=3;i<=n;i++){for(int j=1;j<i;j++){dp[i]=Math.max(dp[i], Math.max(j*dp[i-j], j*(i-j)));}}return dp[n];}
}

⚠️本题的优化思路：其实将对于j的遍历条件改为: j<i-1可以节省一步计算，因为如果让j=i-1，其实在 j = 1的时候，这一步就已经拆出来了，属于重复计算，所以 j < i - 1。

更优化一步，可以这样：

for (int i = 3; i <= n ; i++) {for (int j = 1; j <= i / 2; j++) {dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}
}

因为拆分一个数i使之乘积最大，比如i=x+(i-x) dp[i]=x(i-x)=xi-x^2，这时是一个向下的抛物线，最大点为x/2

96.不同的叉搜索树

给定一个整数 n，求以 1 ... n 为节点组成的二叉搜索树有多少种？

示例:

这道题要求能构造多少二叉搜索树。二叉搜索树是有一定规律的，其中序遍历是有序的。按照示例所给，可以先从1开始遍历，看以i为根节点能构造出多少子树。其实一开始还是没有什么思路，主要是递推公式不太好想，所以准备按照五部曲依次思考一下：

1. 确定dp数组以及下标的含义：dp[i]为有i个节点时能构造的二叉搜索树个数。
2. 确定递推公式：目前还没有什么思路。
3. dp数组如何初始化：若n=1，则dp[1]毫无疑问是1，若n=2，则有两种构造方法，一种是以1为根节点，左子树为空，右子树为2；一种是以2为根节点，左子树为1，右子树为空，所以dp[2]=2；n=3就是示例中所给情况，可以看到，如果以1为根节点，则左子树一定为空的，右子树有两种可能，分别是以2和3为子树根节点。若以2为根节点，则左右子树各有一个节点，有一种可能，若以3为根节点，则右子树为空，左子树有两种可能，分别是以1和2为子树根节点。

当分析到如何初始化的时候，已经渐渐有了关于推导递推公式的雏形，接下来可以捋一下思路：

当n=1时：只有一个节点，不附图了

当n=2时：如下

当n=3时，有三种大的情况：

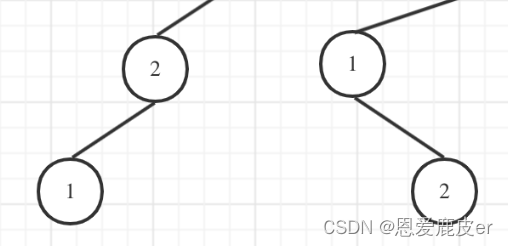
1. 以1为根节点：因为此题本质求的是树的形状的可能性，所以跟具体的数值关系不大，如果把1去掉来看，可以看到，其实剩下的形状和n=2的时候是一样的：
2. 以2为根节点：左边节点1，右边节点3
3. 以3为根节点：去掉3，剩下的形状和n=2的时候也是一样的：

因此

• 有2个元素的搜索树数量就是dp[2]。
• 有1个元素的搜索树数量就是dp[1]。
• 有0个元素的搜索树数量就是dp[0]。

可以这样推导：

1. 以1为头节点的搜索树个数=右子树有2个元素搜索树数量*左子树有0个元素搜索树数量
2. 以2为头节点的搜索树个数=右子树有1个元素搜索树数量*左子树有1个元素搜索树数量
3. 以3为头节点的搜索树个数=右子树有0个元素搜索树数量*左子树有2个元素搜索树数量

那么n=3时，dp[3]就是上面三种情况的搜索树个数之和，即dp[3]=dp[2]*dp[0]+dp[1]*dp[1]+dp[0]*dp[2] ，

拓展到i就是：不断地累加：dp[以j为头结点左子树节点数量]*dp[以j为头结点右子树节点数量]，j的范围为[1, i]

所以递推公式为：dp[i]+=dp[j-1]*dp[i-j]，因此下面完整的五部曲为：

1. 确定dp数组以及下标的含义：有i个节点时能构造的二叉搜索树个数
2. 确定递推公式：dp[i]+=dp[j-1]*dp[i-j]
3. dp数组如何初始化：要注意，从定义上来讲，空节点也是一棵二叉树，也是一棵二叉搜索树，所以dp[0]=1，这个我一开始弄错了。dp[1]=1
4. 确定遍历顺序：i从1到n，j从1到i
5. 举例推导dp数组：无法手动举更多例子

class Solution {/**确定dp数组以及下标的含义：有i个节点时能构造的二叉搜索树个数确定递推公式：dp[i]+=dp[j-1]*dp[i-j]dp数组如何初始化：dp[1]=1，dp[2]=2确定遍历顺序：i从3到n，j从1到i*/public int numTrees(int n) {int[] dp=new int[n+1];dp[0]=1;dp[1]=1;for(int i=2;i<=n;i++){for(int j=1;j<=i;j++){dp[i]+=dp[j-1]*dp[i-j];}}return dp[n];}
}

这篇关于Leetcoder Day36｜ 动态规划part03的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---