数字CMOS集成电路——超级缓冲器设计

超级缓冲器设计

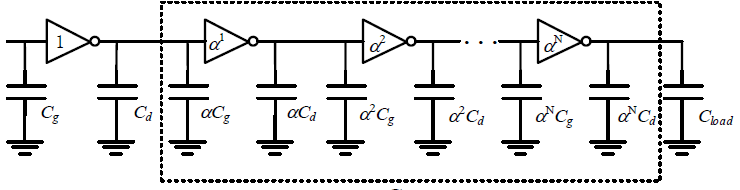
超级缓冲器——驱动大电容、减少传输延迟时间

# Cload = 50			# 负载电容/pF
# Ci = Cg = 5 / 1000	# 等效反相器（第一级）的输入电容（栅极电容）/pF
# tp0 = 35				# 第一级反相器的本征延时/ps，无负载的情况下的延迟
# tp_inv = 70			# 环形振荡器单级的延迟时间/ps，负载为相同尺寸的反相器
# Cd = Cgwhile(1):Cload = int(input("请输入负载电容容值（pF）："))Ci = int(input("请输入输入电容容值（fF）："))Cd = Cg = Ci = Ci / 1000tp_inv =int(input("请输入第一级反相器链构成的环形振荡器的单级延迟时间（ps）："))while(1):choose = str(input("是否指定设计级数（Y/N）:"))if choose == 'Y':N = int(input('N = ')) 		# 级数 一般小于5a = pow(Cload / Cg, 1 / (N + 1))t_total = (N+1)*tp_inv*((Cd+a*Cg)/(Cd+Cg))/1000print("when N = {}, a = {:.2f}, total delay time: {:.2f}ns".format(N, a, t_total))elif choose == 'N':time = [0]a_list = [0]for N in range(1,10):a = pow(Cload / Cg, 1 / (N + 1))	# 比例因子t_total = (N+1)*tp_inv*((Cd+a*Cg)/(Cd+Cg))/1000 	#nsa_list.append(a)time.append(t_total)# print("when N = {}, a = {:.3f}, total delay time: {:.3f}ns".format(N, a_list[N], time[N]))del time[0]del a_list[0]N_min = time.index(min(time))print("when N = {}, a = {:.2f}, total delay time: {:.2f}ns".format(N_min + 1, a_list[N_min], time[N_min]))else:print("请输入正确的执行指令！")

在Cload=50pF，Cin=5fF时，单级延迟70ps的情况下执行以上代码段。如果指定超级缓冲器的级数为2，则可以得到最小延迟的反相器的比例因子为21.45；如果不指定级数，计算出延迟时间最小的设计指标：级数为6与比例因子为3.73。详情如下所示。

E:\work_program\PYTHON\ex_old>python d_cmos_INV_chains_chap6.py
请输入负载电容容值（pF）：50
请输入输入电容容值（fF）：5
请输入第一级反相器链构成的环形振荡器的单级延迟时间（ps）：70
是否指定设计级数（Y/N）:Y
N = 2
when N = 2, a = 21.54, total delay time: 2.37ns
是否指定设计级数（Y/N）:Y
N = 4
when N = 4, a = 6.31, total delay time: 1.28ns
是否指定设计级数（Y/N）:Y
N = 8
when N = 8, a = 2.78, total delay time: 1.19ns
是否指定设计级数（Y/N）:N
when N = 6, a = 3.73, total delay time: 1.16ns
是否指定设计级数（Y/N）:

此例旨在用python完成简单的计算和判断求最优解。如采用数值解法，需要对延迟时间与级数或者比例因子之间求微分，进而求得取最值的条件，本例中采用枚举计算，利用级数与比例因子之间的关联，算出各级情况对应的传输延迟时间，然后比较大小后得到最小值。