【数据结构与算法】常见排序算法（Sorting Algorithm）

2024-03-03 13:20
文章标签 算法 常见 数据结构 排序 algorithm sorting

本文主要是介绍【数据结构与算法】常见排序算法（Sorting Algorithm），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

  • 相关概念
  • 1. 冒泡排序（Bubble Sort）
  • 2. 直接插入排序（Insertion Sort）
  • 3. 希尔排序（Shell Sort）
  • 4. 直接选择排序（Selection Sort）
  • 5. 堆排序（Heap Sort）
  • 6. 快速排序（Quick Sort）
    • 6.1 hoare快排（最早的快排方法）
    • 优化快排（重要）
      • 1. 减少函数递归的栈帧开销（虽然不用，但必须了解）
      • 2.三位取中法取基准值（重点）
    • 6.2 挖坑法快排
    • 6.3 双指针法快排
    • 6.4 非递归快排
    • 快速排序的排序速度比较（包含测试代码）
  • 7. 归并排序（Merge Sort）

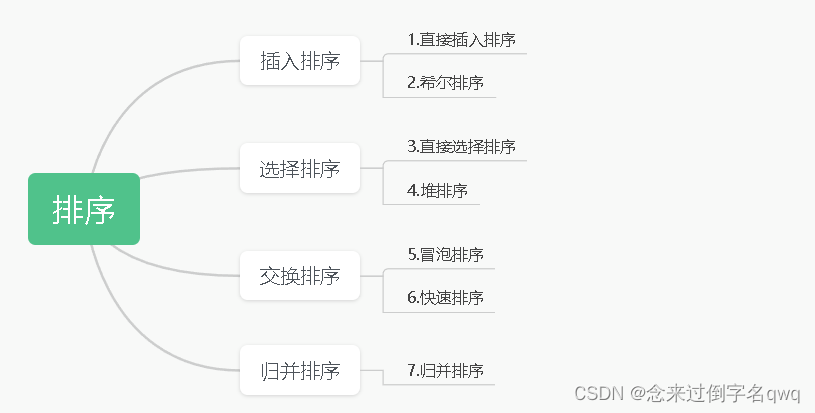
在这里插入图片描述

相关概念

  1. 排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。
  2. 稳定性：说简单点就是有相同值时，排序后这些相同值互相顺序没发生变化则称为稳定的排序算法。假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。
  3. 内部排序：数据元素全部放在内存中的排序（重点）。
  4. 外部排序：数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序（了解）。

常见排序算法时间、空间、稳定性：

  1. 直接插入排序：O(n2)，正常情况下最快的O(n2)排序算法，稳定。
  2. 希尔排序：O(n1.3)，比O(n*log2n)慢一点点，不稳定。
  3. 直接选择排序：O(n2)，比冒泡快，比插入慢，不稳定。
  4. 堆排序：O(n*log2n)，不稳定。
  5. 冒泡排序：O(n2)，稳定。
  6. 快速排序： O(n*log2n)，不稳定，空间O(log2n)。
  7. 归并排序 O(n*log2n)，稳定，空间O(n)。

排序不特别说明，则排序以升序为例。
时间复杂度不特别说明，则默认最坏时间。
空间复杂度不特别说明，则默认O(1)。

1. 冒泡排序（Bubble Sort）

思想：两两比较，再交换。前一个值比后一个值大，交换两个值。
在这里插入图片描述
在这里插入图片描述
优化冒泡排序，冒泡排序优化版：
在这里插入图片描述

void BubbleSort(int* a, int n) 
{int sortBorder = n - 1;int lastExchange = 0; for (int i = 0; i < n - 1; ++i) {bool isSorted = true; for (int j = 0; j < sortBorder; ++j) {if (a[j] > a[j + 1]) {Swap(&a[j], &a[j + 1]);isSorted = false;lastExchange = j;}}if (isSorted) {break;}sortBorder = lastExchange;}
}
void Swap(int* px, int* py) 
{int tmp = *px;*px = *py;*py = tmp;
}

2. 直接插入排序（Insertion Sort）

思想：类似将扑克牌排序的过程，数据越有序，排序越快。
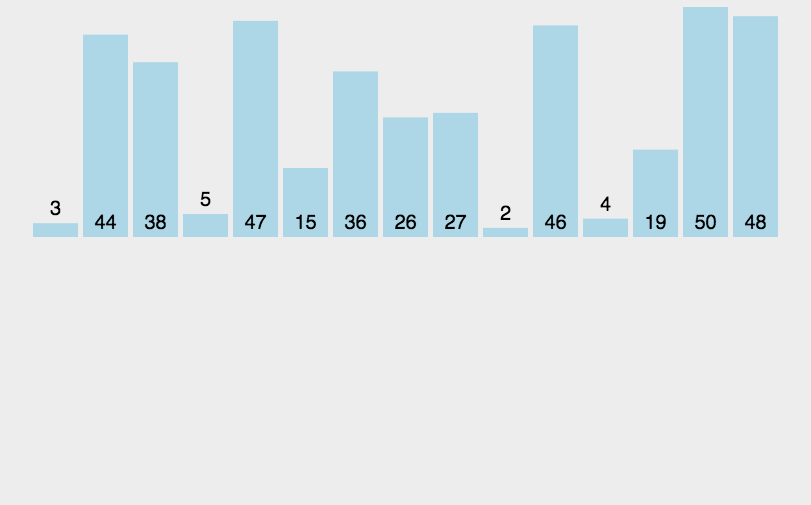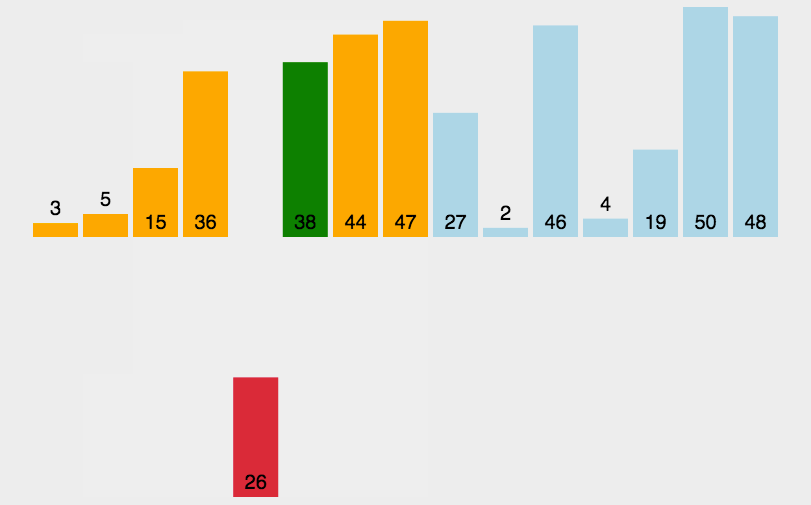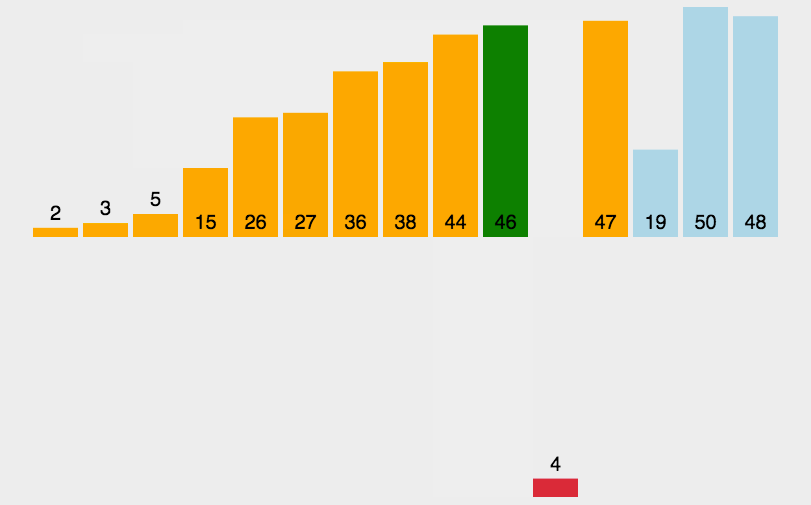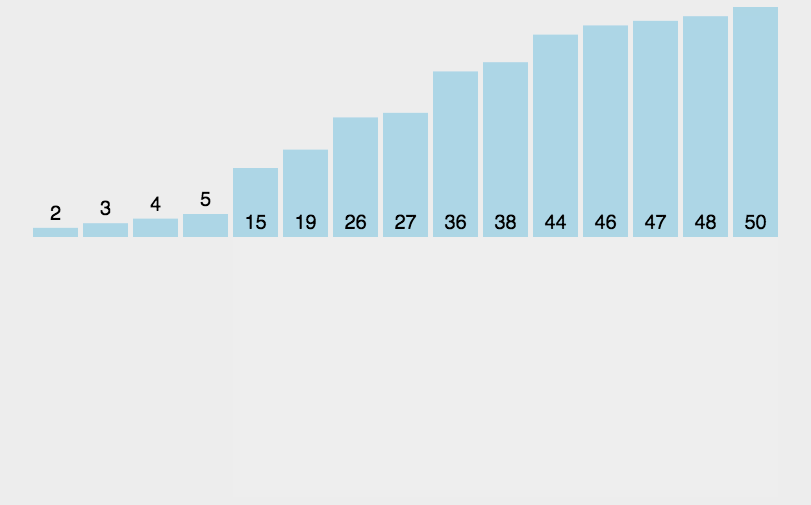
在这里插入图片描述
在这里插入图片描述

void InsertionSort(int* a, int n)
{for (int i = 0; i < n - 1; ++i){int end = i;int insertVal = a[end + 1];while (end >= 0 && insertVal < a[end]){a[end + 1] = a[end];--end;}a[end + 1] = insertVal;}
}

直接插入排序O(n*n)，n方的排序中，直接插入排序是最有价值的。其它的如冒泡，直接选择排序等与直接插入排序一样N方的排序都是五十步和百步的区别，总体来看没啥区别，都不如直接插入排序，看以下几点分析以及排序时间比较，再就是大家自己编一串数据走查一下排序过程即可发现。

1.排升序而数据大致是降序，或排降序而数据大致是升序情况下，直接插入排序的时间复杂度是O(n*n)，因为比较挪数据次数是等差数列之和。

2.数据大致有序，且排序顺序与数据顺序一致情况下，直接插入排序的时间复杂度是O(n)，因为比较挪数据次数较少（不进入while循环）。比如排升序，而数据也大致也是升序状态（较为有序 或 直接就是有序的）。

3.虽然直接插入排序与冒泡排序的时间复杂度是同一个量级，但不谈上面第一种情况，
正常大多都是数据随机排列情况下前者比后者快很多，这时比较挪数据次数不会是等差数列之和，中间一般多少会有一部分是有序的，有那么几趟是不进入while循环的，比较挪数据次数当然是比等差数列之和要少的。虽然还是O(n*n)的量级，但明显是比冒泡快，至于快多少则是看有序的数据多不多（极限就是第二种情况）。

10w个数据 排序速度对比：
在这里插入图片描述

release环境是发布版本环境，对代码是有很大优化的，优化点大致是：

  1. 相比于debug环境，release环境生成的目标文件包含很少调试信息甚至没有调试信息。
  2. 减少了很多消耗性能或不必要的操作，不对代码进行边界检查，空指针检查、assert断言检查等。
  3. 特别是对递归优化巨大，也就是对函数栈帧的创建/栈的消耗优化很大，比如对于debug环境下栈溢出的程序，切换成release则不会造成栈溢出。

博主水平有限，不知道更多相关细节或是底层原理，如有错误恳请指正。

3. 希尔排序（Shell Sort）

希尔排序是直接插入排序的优化版，对于直接插入排序而言，数据越有序，排序越快，希尔排序正是借助直接插入排序的特点进行了优化。

思想：先对数据分组进行几次预排序（对数据分组进行直接插入排序），使数据形成较为有序的情况，最后整体进行一趟直接插入排序即可完成排序。

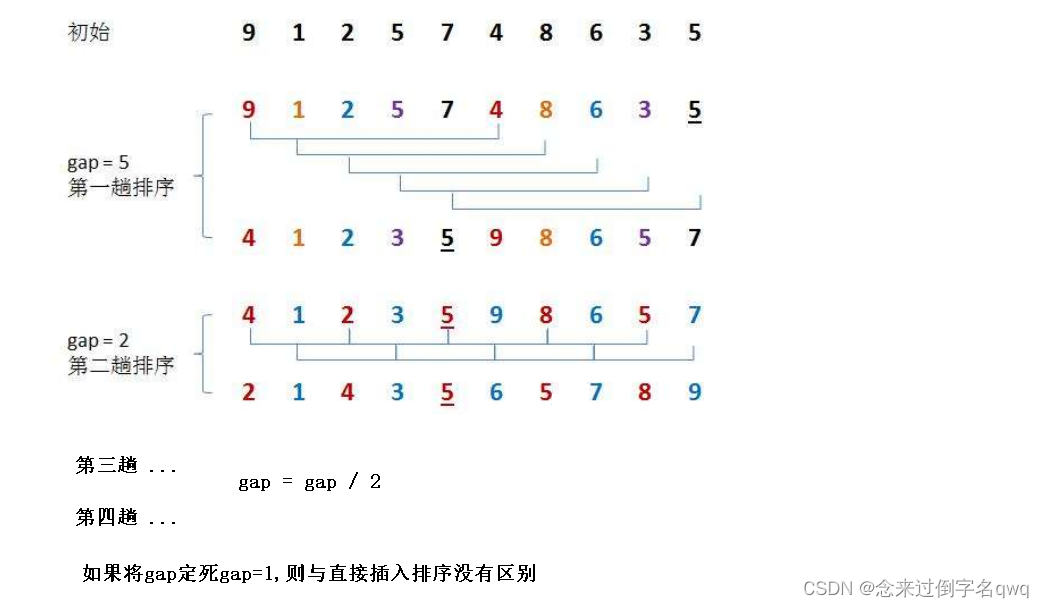
在这里插入图片描述

void ShellSort(int* a, int n) 
{int gap = n; while (gap > 1) {gap = gap / 3 + 1; // gap / 2也可for (int j = 0; j < n - gap; ++j) {int end = j;int insertVal = a[end + gap];while (end >= 0 && insertVal < a[end]) {a[end + gap] = a[end];end -= gap;}a[end + gap] = insertVal;}}
}

  1. 希尔排序不好计算确切的时间复杂度，有牛人通过大量实验证明平均时间复杂度大致为O(n^1.3)，比O(n*logn)要慢一点点，但两者差不多是同一量级。

  2. gap>1时是预排序，gap=1时等于直接插入排序。

  3. gap的取值，gap/2或gap/3+1是当前主流，也被认为是gap最好的取值。gap相当于划分多少组进行预排序，如果定死gap=1则与直接插入排序无异。gap/2或gap/3+1则是划分每组多少个数进行预排序，gap/3+1中的+1是因为要保证最后一组排序时gap=1进行直接插入排序操作。严格来说只要能保证最后一趟gap=1，无论gap除以几加几，都算是希尔排序。

  4. 每一组预排序后，都会逐渐加大数据的有序情况。后面几组预排序虽然每组划分的数据多了（gap逐渐减小间隔变小了），也就是比较次数变多了，但经过前面的预排序后数据渐渐有序，实际不会进行过多的比较挪数据操作，每前一次预排序都为后一次预排序减轻压力。

速度对比（毫秒）：
在这里插入图片描述

4. 直接选择排序（Selection Sort）

每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，逐步向后存放。
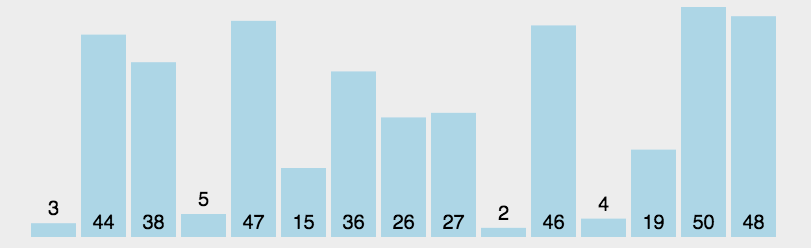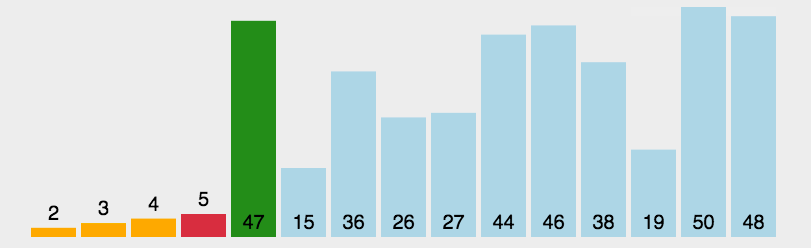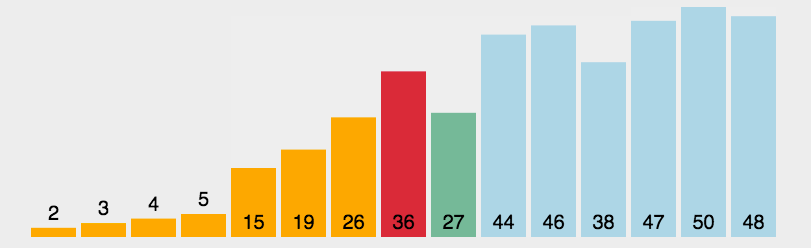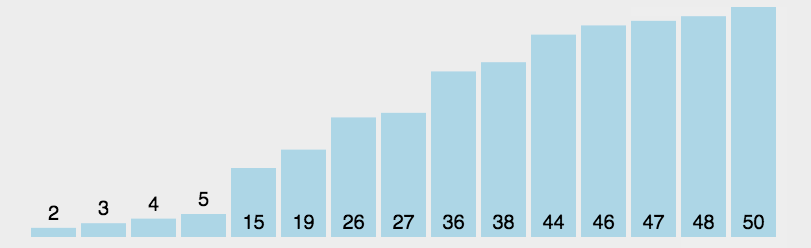
在这里插入图片描述
在这里插入图片描述

数据较为有序的情况下，直接选择排序选要比冒泡、直接插入排序慢。

void SelectionSort(int* a, int n)
{int begin = 0, end = n - 1;while (begin < end){int min = begin, max = end;for (int i = begin; i <= end; ++i){if (a[i] < a[min]) min = i;if (a[i] > a[max]) max = i;}Swap(&a[begin], &a[min]);if (max == begin){max = min;}Swap(&a[end], &a[max]);++begin; --end;}
}

在优化版中，必须有这样一个判断max==begin，并更新max的下标值！最小的数a[min]换到了左边begin位置，如果最大的数的下标max正好等于begin，那就出现这种问题：最大的数a[max]已经被换到min下标位置了，即a[min]才是最大数；而本来a[max]是最大的数，由于max==begin，而经过前面a[begin]与a[min]交换的影响，导致a[begin]/a[max]变成了最小的数，不加判断并更新max的后果是把最小的数放在右边end位置了。

5. 堆排序（Heap Sort）

了解堆请看：文章 堆 / 堆排序 / TopK问题（Heap）

时间复杂度O(nlog2n)，排序速度与希尔差不多。也可以向上调整建堆，但比向下调整建堆要慢一些。

void HeapSort(int* a, int n)
{for (int parent = (n - 1 - 1) / 2; parent >= 0; --parent) {AdjustDown(a, n, parent);}for (int end = n - 1; end > 0; --end){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);}
}
/* 将堆向下调整为大堆 */
void AdjustDown(int* a, int size, int parent)
{int child = parent * 2 + 1; // 选出较大子节点child = child + 1 < size && a[child + 1] > a[child]? child + 1 : child;while (child < size && a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child; // 重复往下child = parent * 2 + 1;child = child + 1 < size && a[child + 1] > a[child]? child + 1 : child;}
}

parent初始为最后一个非叶子节点（多一个 -1 的原因），
向下调整（建大堆），往堆顶方向走把所有非叶子结点调整一遍。

堆顶最大值与堆底较小值交换，然后排除这个堆底的最大值(a[end])，
剩下的作为堆，从堆顶较小值开始向下调整为大堆（–end一步步排除新的最大值a[end]）。

10w个数据，排序速度对比：
在这里插入图片描述
堆排序时间复杂度严格来算：

  1. 向上调整建堆O(nlogn) + 排序O(nlong)：O(2n*2logn)。
  2. 向下调整调整建堆O(n) + 排序O(nlogn)：O(2n*logn)。

所以说希尔排序O(n1.3)比O(n*log2n)要慢些，但却是同一量级。不过堆排序的时间复杂度严格来说比真正的O(nlog2n)要慢一点点，所以希尔排序与堆排序的速度相同。

6. 快速排序（Quick Sort）

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法。

6.1 hoare快排（最早的快排方法）

基本思想：取待排序数据中的某个元素作为基准值，将数据分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后左右子序列重复该过程进行分割，直到所有元素都排列在相应位置上为止。
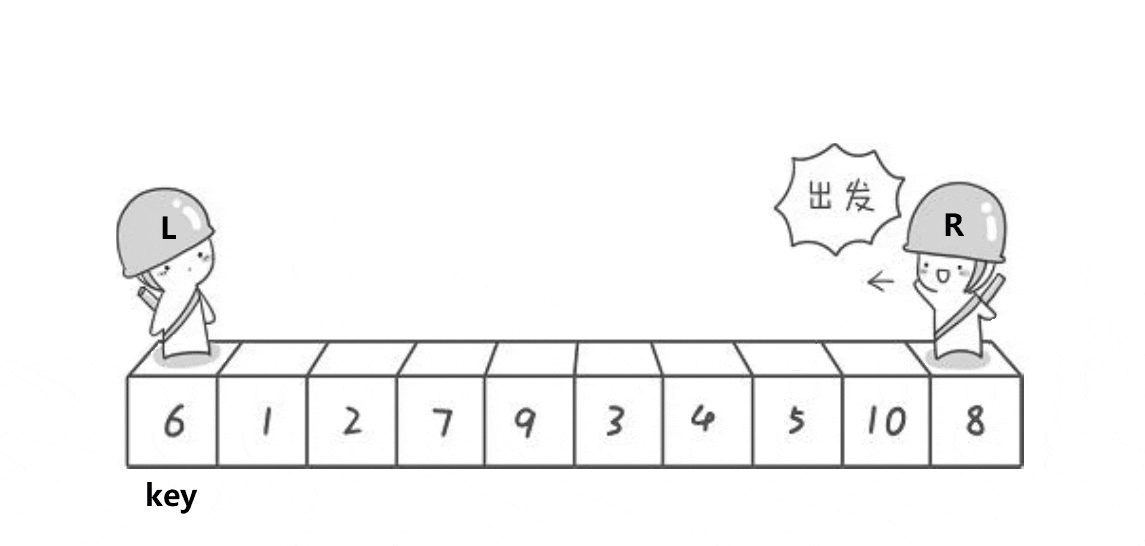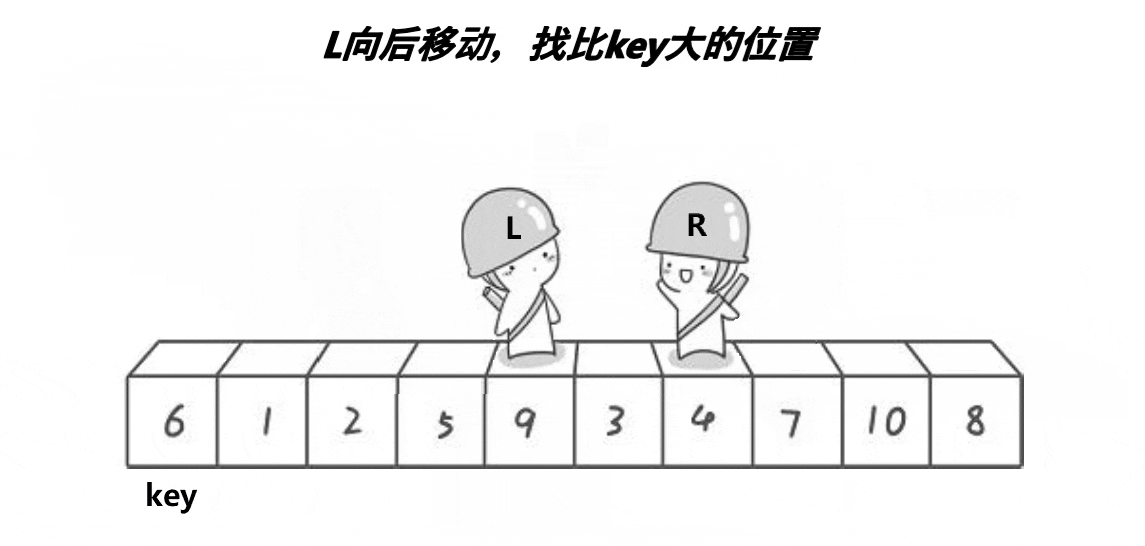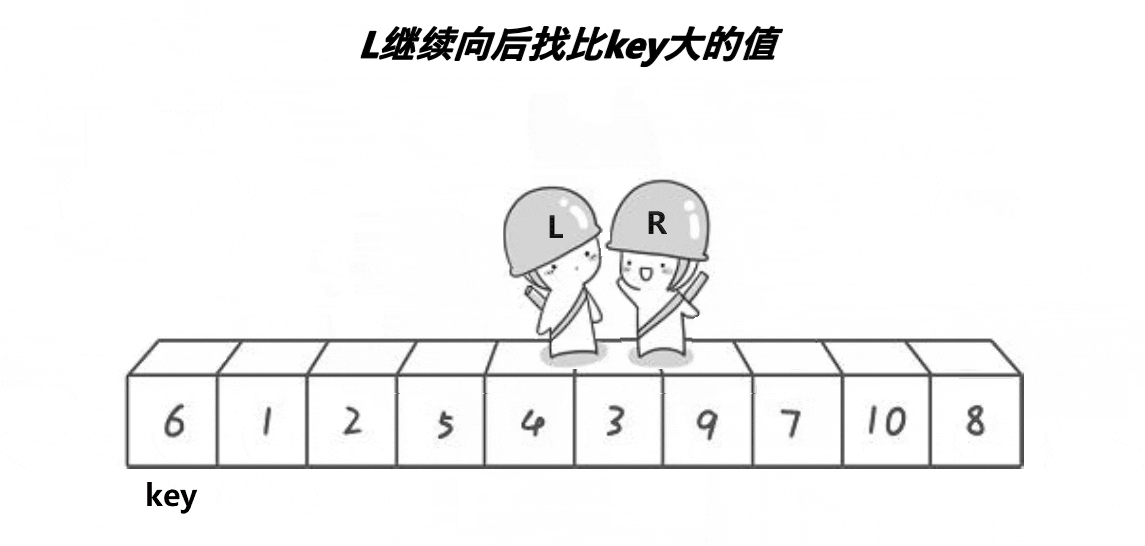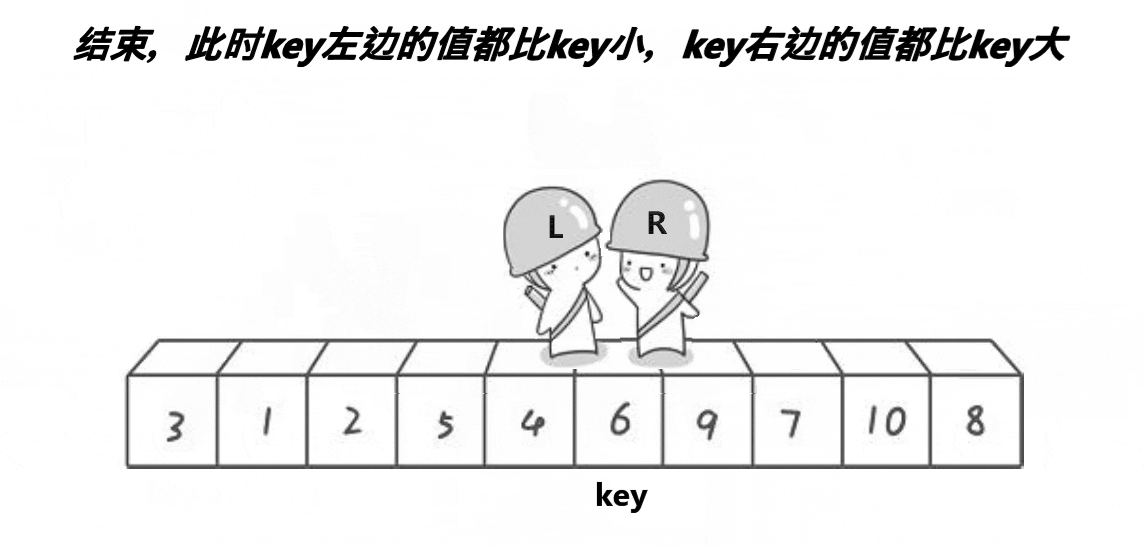
在这里插入图片描述

// 1.hoare递归（最早的快排方法）
void QuickSort1(int* a, int begin, int end)
{if (begin < end) {int left = begin;int right = end;int keyi = begin; // 基准值（下标）while (left < right) {	/* 必须加上left<right防止内循环越界；>=而不是>，<=而不是<，防止重复值死循环。*/while (left < right && a[right] >= a[keyi]) {--right; // 找小的}while (left < right && a[left] <= a[keyi]) {++left; // 找大的}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);QuickSort0(a, begin, left - 1); // 左区间序列QuickSort0(a, left + 1, end); // 右区间序列}
}

基准值的取法：

  1. 取序列第一个数据，需要右指针right先走（学习时往往采用的方式，上面动图演示也是基于这个方式）；或取序列最后一个数据，需要左指针left先走（本质与前者没区别）。
  2. 三位取中法：key、left和right中取第二大的值作为基准值。（这是优化版，推荐）

优化快排（重要）

1. 减少函数递归的栈帧开销（虽然不用，但必须了解）

优化hoare快排的递归开销：递归树最后两三层（小区间）改用插入排序，减少大量函数栈帧内存消耗。该优化在debug环境下确实能优化，在逻辑上也确实能优化，但release环境同样也对递归进行了优化，而且优化力度只会更大，所以小区间使用插入排序减少递归栈帧的优化方案或许起不到效果。

例如一颗满二叉树，可以看到最后两三层的数量是最多的：
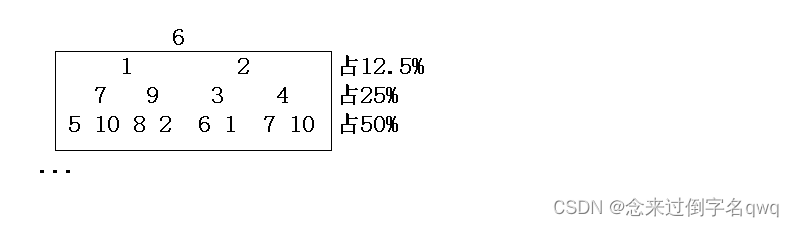
在这里插入图片描述
对于hoare快排划分左右区间同理：
在这里插入图片描述

#define RECUR_MAX 10
void QuickSortX(int* a, int begin, int end)
{if (begin < end){if (end - begin + 1 <= RECUR_MAX){InsertionSort(a, end - begin + 1);}else{int left = begin;int right = end;int keyi = begin; // 基准值（下标）while (left < right){	/* 必须加上left<right防止内循环越界；>=而不是>，<=而不是<，防止重复值死循环。*/while (left < right && a[right] >= a[keyi]) {--right; // 找小的}while (left < right && a[left] <= a[keyi]) {++left; // 找大的}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);QuickSort0(a, begin, left - 1); // 左区间序列QuickSort0(a, left + 1, end); // 右区间序列}}
}

2.三位取中法取基准值（重点）

该优化提升非常大，主要是优化对较为有序的数据进行排序的情况。先看例子：一个较为有序的序列 1 2 3 4 7 6 8 10 9 对于这组数据，对于现在没有使用三位取中的快排而言，前面几趟排序是比较难受的。

比如第一趟，right一直不到比key要大的值，找最后搞得–right来到了key的位置，这就导致没有左区间，右区间从2开始，数据越是有序，快排速度越慢，最慢时退化到O(n2)。
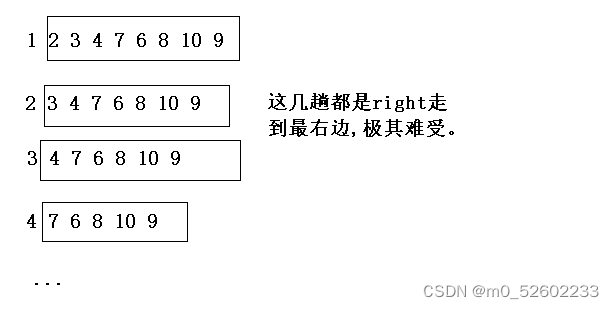
在这里插入图片描述
解决办法就是不要直接取第一位作为基准值，从begin、mid和end之间选出第二大的值作为基准值。
在这里插入图片描述
每趟排序前先三位取中做交换，这样就不至于面对这种情况，每趟排序right都走到最右边。

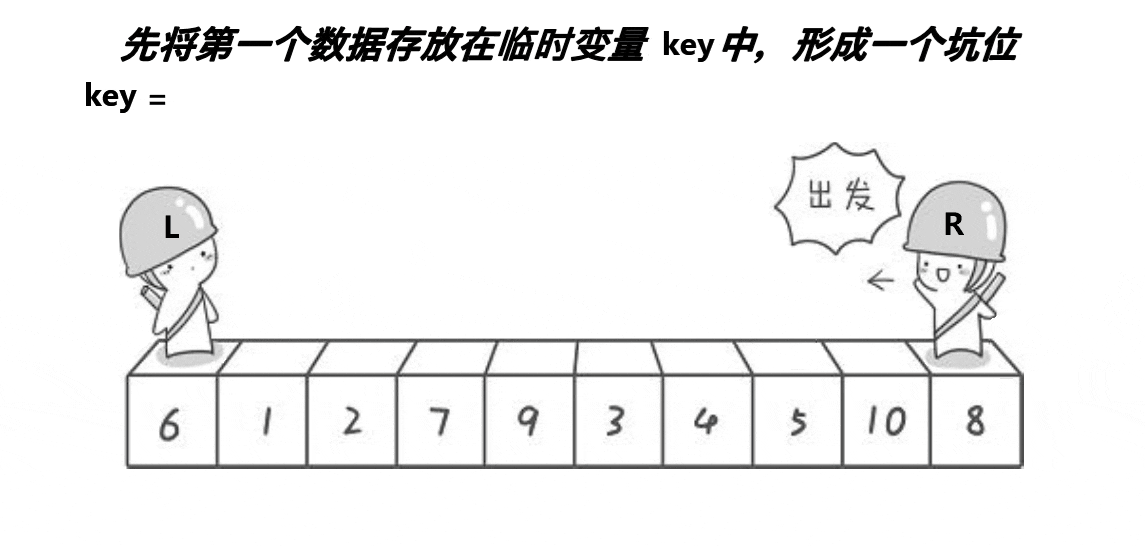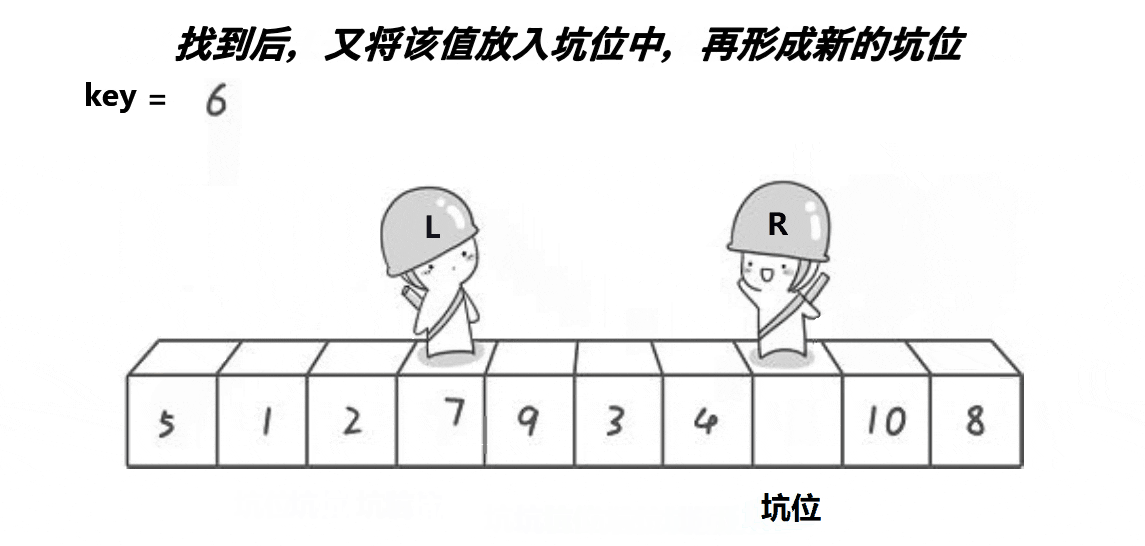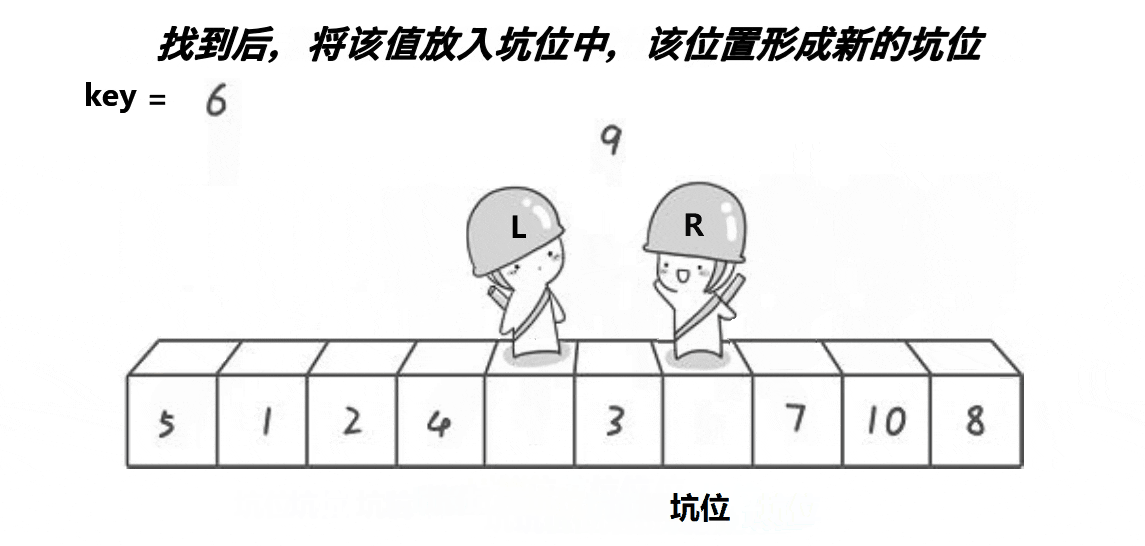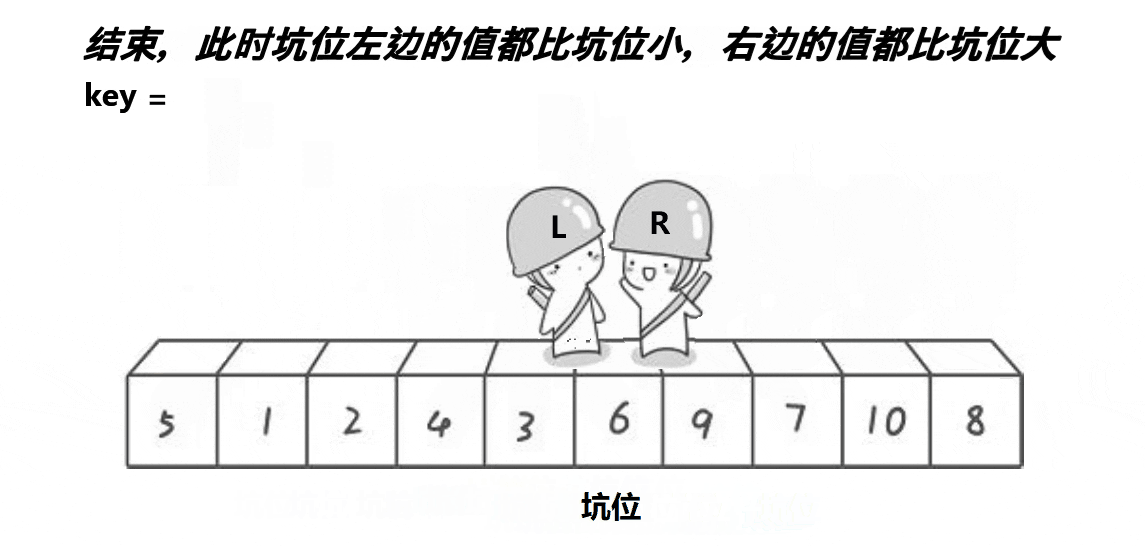
6.2 挖坑法快排

该方法思想与hoare版差不多，算是hoare版的改进，可能更好理解一些，但排序速度比起hoare版没啥大变化，差不多。
在这里插入图片描述

void QuickSort2(int* a, int begin, int end)
{if (begin < end){if ((end - begin) + 1 <= RECUR_MAX) {InsertionSort(a + begin, (end - begin) + 1);}else{int midi = MidIndex(a, begin, end);Swap(&a[begin], &a[midi]);int left = begin;int right = end;int key = a[begin];int pos = begin;while (left < right){while (left < right && a[right] >= key) {--right;}a[pos] = a[right];pos = right;while (left < right && a[left] <= key) {++left;}a[pos] = a[left];pos = left;}a[pos] = key;QuickSort2(a, begin, pos - 1);QuickSort2(a, pos + 1, end);}}
}

6.3 双指针法快排

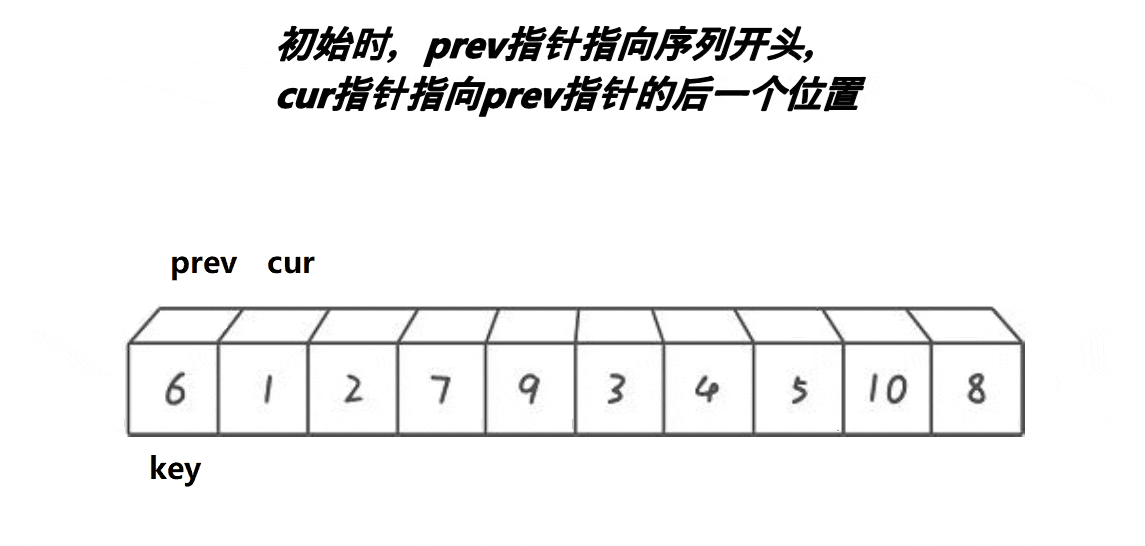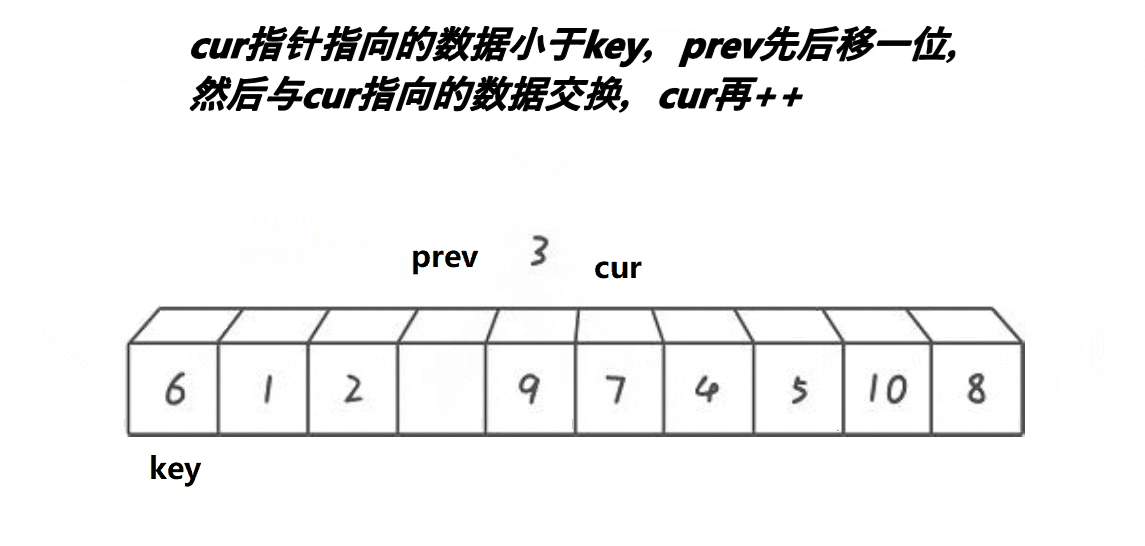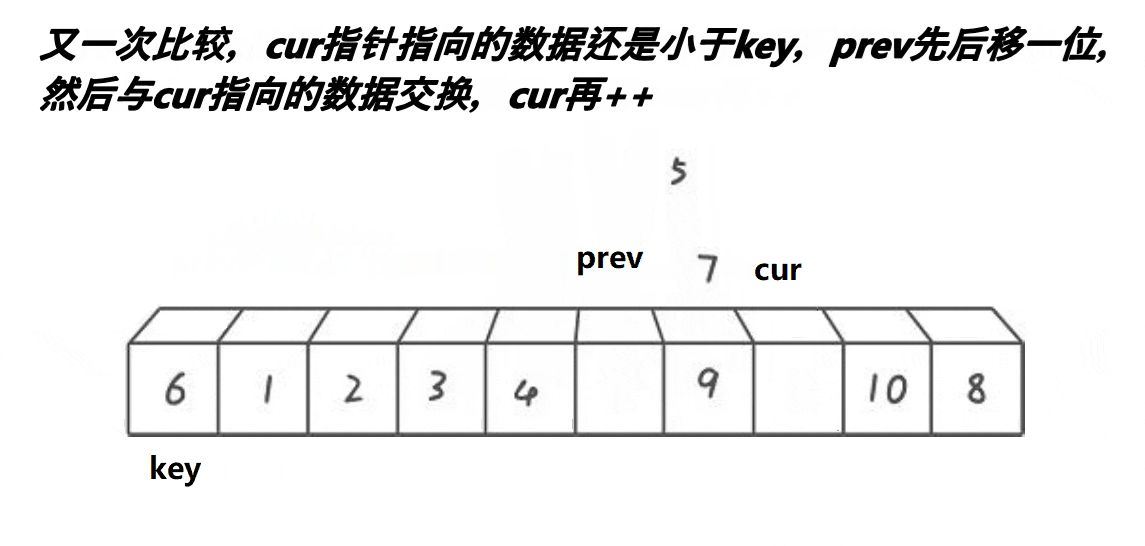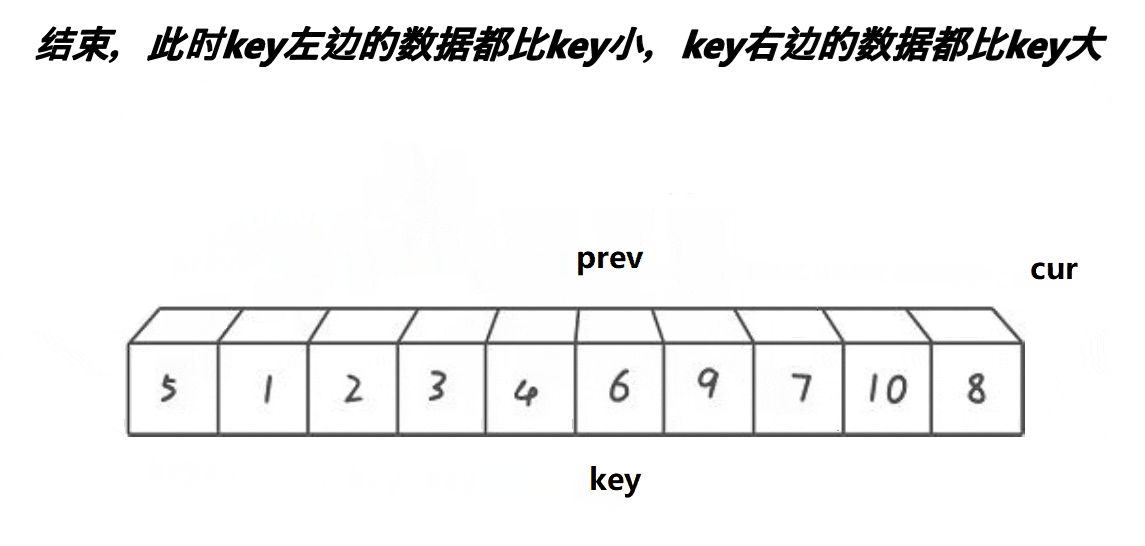
在这里插入图片描述

void QuickSort3(int* a, int begin, int end)
{if (begin < end){int midi = MidIndex(a, begin, end);Swap(&a[begin], &a[midi]);int keyi = begin;int pre = begin;int cur = begin + 1;while (cur <= end){if (a[cur] <= a[keyi]) {++pre;Swap(&a[pre], &a[cur]);}++cur;}Swap(&a[keyi], &a[pre]);keyi = pre;QuickSort3(a, begin, keyi - 1);QuickSort3(a, keyi + 1, end);}
}

6.4 非递归快排

需要借助栈实现，本质与递归一样，递归也是栈帧的开辟与销毁。

快速排序的排序速度比较（包含测试代码）

500w个数据，毫秒为单位：
在这里插入图片描述
1000w个数据：
在这里插入图片描述

#include "Sort.h"void TestPerformance();int main() {TestPerformance();
}void TestPerformance() {const int N = 10000000;//int* a1 = (int*)malloc(sizeof(int) * N);//int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);//int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a10 = (int*)malloc(sizeof(int) * N);int* a11 = (int*)malloc(sizeof(int) * N);int* a12 = (int*)malloc(sizeof(int) * N);srand((unsigned int)time(0));for (int i = 0; i < N; i++) {//a1[i] = rand();//a2[i] = a1[i];a3[i] = rand();//a4[i] = a1[i];a5[i] = a3[i];a6[i] = a3[i];a10[i] = a3[i];a11[i] = a3[i];a12[i] = a3[i];}//int begin1 = clock();//BubbleSort(a1, N);//int end1 = clock();//int begin2 = clock();//InsertionSort(a2, N);//int end2 = clock();int begin3 = clock();ShellSort(a3, N);int end3 = clock();//int begin4 = clock();//SelectionSort(a4, N);//int end4 = clock();int begin5 = clock();HeapSort(a5, N);int end5 = clock();int begin6 = clock();QuickSort1(a6, 0, N - 1);int end6 = clock();int begin10 = clock();QuickSort2(a10, 0, N - 1);int end10 = clock();int begin11 = clock();QuickSort3(a11, 0, N - 1);int end11 = clock();int begin12 = clock();QuickSort3(a12, 0, N - 1);int end12 = clock();//printf("BubbleSort: %d\n", end1 - begin1);//printf("InsertionSort: %d\n", end2 - begin2);printf("ShellSort: %d\n", end3 - begin3);//printf("SelectionSort: %d\n", end4 - begin4);printf("HeapSort: %d\n", end5 - begin5);printf("QuickSort1: %d\n", end6 - begin6);printf("QuickSort2: %d\n", end10 - begin10);printf("QuickSort3: %d\n", end11 - begin11);printf("QuickSortNonRecur: %d\n", end12 - begin12);
}

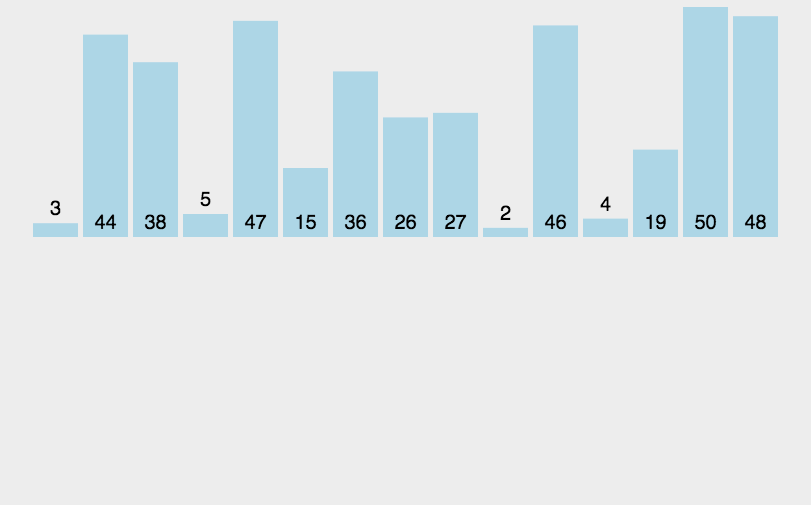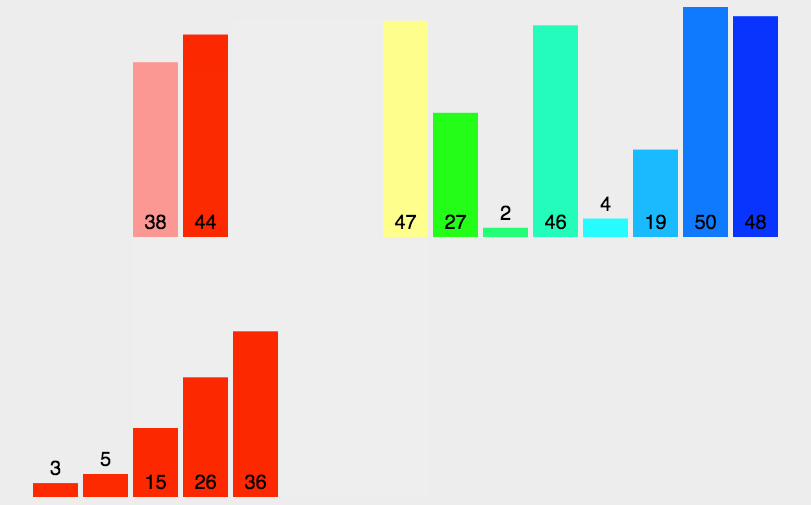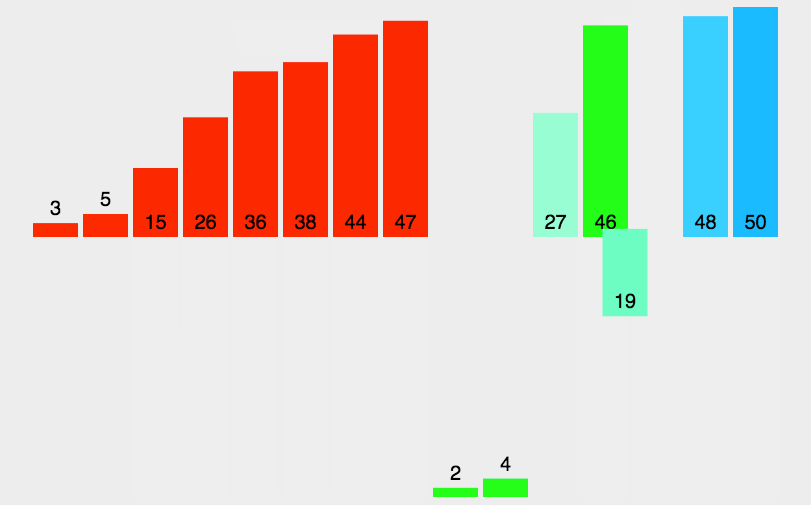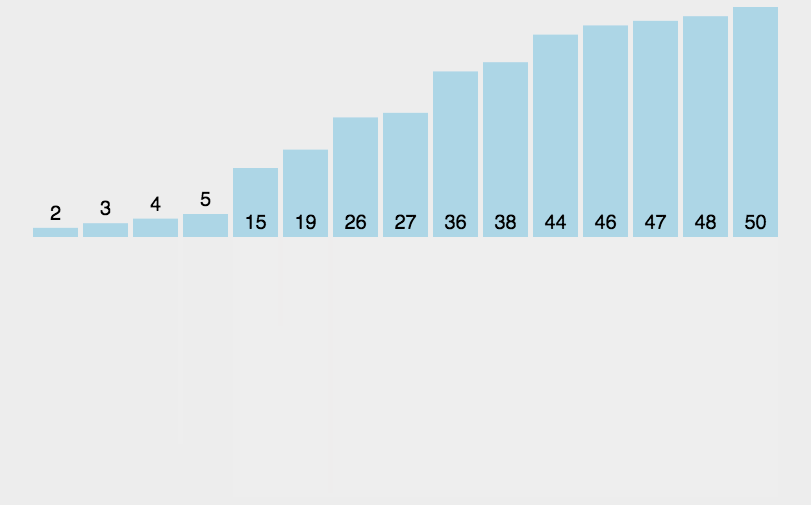
7. 归并排序（Merge Sort）

在这里插入图片描述

这篇关于【数据结构与算法】常见排序算法（Sorting Algorithm）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/769732。

相关文章

Pytest多环境切换的常见方法介绍

Pytest多环境切换的常见方法介绍

《Pytest多环境切换的常见方法介绍》Pytest作为自动化测试的主力框架,如何实现本地、测试、预发、生产环境的灵活切换,本文总结了通过pytest框架实现自由环境切换的几种方法,大家可以根据需要进... 目录1.pytest-base-url2.hooks函数3.yml和fixture结论你是否也遇到过
阅读更多...
springboot+dubbo实现时间轮算法

springboot+dubbo实现时间轮算法

《springboot+dubbo实现时间轮算法》时间轮是一种高效利用线程资源进行批量化调度的算法,本文主要介绍了springboot+dubbo实现时间轮算法,文中通过示例代码介绍的非常详细,对大家... 目录前言一、参数说明二、具体实现1、HashedwheelTimer2、createWheel3、n
阅读更多...
Mybatis 传参与排序模糊查询功能实现

Mybatis 传参与排序模糊查询功能实现

《Mybatis传参与排序模糊查询功能实现》：本文主要介绍Mybatis传参与排序模糊查询功能实现,本文通过实例代码给大家介绍的非常详细,感兴趣的朋友跟随小编一起看看吧... 目录一、#{ }和${ }传参的区别二、排序三、like查询四、数据库连接池五、mysql 开发企业规范一、#{ }和${ }传参的
阅读更多...
C/C++错误信息处理的常见方法及函数

C/C++错误信息处理的常见方法及函数

《C/C++错误信息处理的常见方法及函数》C/C++是两种广泛使用的编程语言,特别是在系统编程、嵌入式开发以及高性能计算领域,：本文主要介绍C/C++错误信息处理的常见方法及函数,文中通过代码介绍... 目录前言1. errno 和 perror()示例：2. strerror()示例：3. perror(
阅读更多...
Go标准库常见错误分析和解决办法

Go标准库常见错误分析和解决办法

《Go标准库常见错误分析和解决办法》Go语言的标准库为开发者提供了丰富且高效的工具,涵盖了从网络编程到文件操作等各个方面,然而,标准库虽好,使用不当却可能适得其反,正所谓工欲善其事,必先利其器,本文将... 目录1. 使用了错误的time.Duration2. time.After导致的内存泄漏3. jsO
阅读更多...
C#数据结构之字符串(string)详解

C#数据结构之字符串(string)详解

《C#数据结构之字符串(string)详解》：本文主要介绍C#数据结构之字符串(string),具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录转义字符序列字符串的创建字符串的声明null字符串与空字符串重复单字符字符串的构造字符串的属性和常用方法属性常用方法总结摘
阅读更多...
MyBatis 动态 SQL 优化之标签的实战与技巧(常见用法)

MyBatis 动态 SQL 优化之标签的实战与技巧(常见用法)

《MyBatis动态SQL优化之标签的实战与技巧(常见用法)》本文通过详细的示例和实际应用场景,介绍了如何有效利用这些标签来优化MyBatis配置,提升开发效率,确保SQL的高效执行和安全性,感... 目录动态SQL详解一、动态SQL的核心概念1.1 什么是动态SQL？1.2 动态SQL的优点1.3 动态S
阅读更多...
SpringBoot实现MD5加盐算法的示例代码

SpringBoot实现MD5加盐算法的示例代码

《SpringBoot实现MD5加盐算法的示例代码》加盐算法是一种用于增强密码安全性的技术,本文主要介绍了SpringBoot实现MD5加盐算法的示例代码,文中通过示例代码介绍的非常详细,对大家的学习... 目录一、什么是加盐算法二、如何实现加盐算法2.1 加盐算法代码实现2.2 注册页面中进行密码加盐2.
阅读更多...
Java时间轮调度算法的代码实现

Java时间轮调度算法的代码实现

《Java时间轮调度算法的代码实现》时间轮是一种高效的定时调度算法,主要用于管理延时任务或周期性任务,它通过一个环形数组（时间轮）和指针来实现,将大量定时任务分摊到固定的时间槽中,极大地降低了时间复杂... 目录1、简述2、时间轮的原理3. 时间轮的实现步骤3.1 定义时间槽3.2 定义时间轮3.3 使用时
阅读更多...
java常见报错及解决方案总结

java常见报错及解决方案总结

《java常见报错及解决方案总结》：本文主要介绍Java编程中常见错误类型及示例,包括语法错误、空指针异常、数组下标越界、类型转换异常、文件未找到异常、除以零异常、非法线程操作异常、方法未定义异常... 目录1. 语法错误 (Syntax Errors)示例 1:解决方案：2. 空指针异常 (NullPoi
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2