PID神经网络原理与MATLAB实现（SISO）

序

最近想实现一下PID神经网络，但是书籍和博客都令人头疼，主要是卡在误差反向传播的计算过程中。找一篇通俗易懂的文章实在不易，最终，只能自己静下心，仔细琢磨。只要每一步在逻辑上都是合理的，我们有理由相信能够得到正确的结果。抱着这样的心态，由浅入深，来实现一下。

一、网络结构定义

简单起见，假设一个受控系统单输入 $u$ 单输出 $x$ ，使用一个PID神经网络来作为控制器，使得系统输出达到目标值 $z$。

其中，$W_{3\times 2}$和$V_{1\times 3}$分别为输入层—隐含层权重矩阵和隐含层—输出层权重矩阵。$y_i$和$y_o$分别是PID计算前后向量。$z,x,u$分别为期望值、实际值和网络输出，都是数。

1.1 前向传播

根据以上结构，容易得出前向传播如下。注意简介起见，第$(k)$次的标注省略。

$$\begin{array}{rl}& y_{i1}=w_{11}z+w_{12}x\\ & y_{i2}=w_{21}z+w_{22}x\\ & y_{i3}=w_{31}z+w_{32}x\end{array}\text{\hspace{1em}(1)}$$

$$\begin{array}{rl}& y_{o1}=y_{i1}\\ & y_{o2}=y_{o2}(k-1)+y_{i2}\\ & y_{o3}=y_{i3}(k)-y_{i3}(k-1)\end{array}\text{\hspace{1em}(2)}$$

$$u=v_{11}{y}_{o1}+v_{12}{y}_{o2}+v_{13}{y}_{o3}\text{\hspace{1em}(3)}$$

不妨设受控对象为一个类似二次函数的时变系统（用于仿真），则输出及损失函数为

$$x=u^2(k)+0.1x(k-1)\text{\hspace{1em}(4)}$$

$$J=\frac{1}{2}(z-x{)}^2\text{\hspace{1em}(5)}$$

1.2 反向传播

前向传播计算完成，以下开始反向传播。首先考虑权重 $V$ 对误差 $J$ 的影响，也即计算 $\frac{\partial J}{\partial V}$，根据前向传递函数关系，易得

$$\begin{array}{rl}\frac{\partial J}{\partial v_{11}}& =\frac{\partial J}{\partial x}\frac{\partial x}{\partial u}\frac{\partial u}{\partial v_{11}}\\ & =-(z-x)\cdot \frac{\partial x}{\partial u}\cdot y_{o1}\end{array}\text{\hspace{1em}(6)}$$

由于受控对象的数学模型往往不知道或者偏导难以计算，中间的 $\frac{\partial x}{\partial u}$ 常用下式子代替

$$\frac{\partial x}{\partial u}=\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\frac{x(k)-x(k-1)}{u(k)-u(k-1)}\text{\hspace{1em}(7)}$$

以下$\frac{\partial x}{\partial u}$皆由式(7)得出，不在赘述。

其中 $\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}(\cdot )$是符号函数，输入正数输出$1$，输入负数输出$-1$，输入$0$输出$0$。使用符号函数的好处是归一化到 $[-1,1]$，避免分母很接近0导致输出很大的问题。

同理易得

$$\frac{\partial J}{\partial v_{12}}=-(z-x)\cdot \frac{\partial x}{\partial u}\cdot y_{o2}\text{\hspace{1em}(8)}$$

$$\frac{\partial J}{\partial v_{13}}=-(z-x)\cdot \frac{\partial x}{\partial u}\cdot y_{o3}\text{\hspace{1em}(9)}$$

接下来，计算真正的难点 $\frac{\partial J}{\partial W}$。

$$\begin{array}{rl}\frac{\partial J}{\partial w_{11}}& =\frac{\partial J}{\partial x}\frac{\partial x}{\partial u}\frac{\partial u}{\partial y_{o1}}\frac{\partial y_{o1}}{\partial y_{i1}}\frac{\partial y_{i1}}{\partial w_{11}}\\ & =-(z-x)\cdot \frac{\partial x}{\partial u}\cdot v_{11}\cdot 1\cdot z\end{array}\text{\hspace{1em}(10)}$$

同理易得

$$\begin{array}{rl}\frac{\partial J}{\partial w_{12}}& =\frac{\partial J}{\partial x}\frac{\partial x}{\partial u}\frac{\partial u}{\partial y_{o1}}\frac{\partial y_{o1}}{\partial y_{i1}}\frac{\partial y_{i1}}{\partial w_{12}}\\ & =-(z-x)\cdot \frac{\partial x}{\partial u}\cdot v_{11}\cdot 1\cdot x\end{array}\text{\hspace{1em}(11)}$$

$$\begin{array}{rl}\frac{\partial J}{\partial w_{21}}& =\frac{\partial J}{\partial x}\frac{\partial x}{\partial u}\frac{\partial u}{\partial y_{o2}}\frac{\partial y_{o2}}{\partial y_{i2}}\frac{\partial y_{i2}}{\partial w_{21}}\\ & =-(z-x)\cdot \frac{\partial x}{\partial u}\cdot v_{12}\cdot \frac{\partial y_{o2}}{\partial y_{i2}}\cdot z\end{array}\text{\hspace{1em}(12)}$$

其中

$$\frac{\partial y_{o2}}{\partial y_{i2}}=\frac{\Delta y_{o2}}{\Delta y_{i2}}=\frac{y_{o2}(k)-y_{o2}(k-1)}{y_{i2}(k)-y_{i2}(k-1)}=\frac{y_{i2}(k)}{y_{i2}(k)-y_{i2}(k-1)}$$

和之前一样，使用符号函数计算可得

$$\frac{\partial y_{o2}}{\partial y_{i2}}=\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\frac{y_{i2}(k)}{y_{i2}(k)-y_{i2}(k-1)}\text{\hspace{1em}(13)}$$

同理

$$\begin{array}{rl}\frac{\partial J}{\partial w_{22}}& =\frac{\partial J}{\partial x}\frac{\partial x}{\partial u}\frac{\partial u}{\partial y_{o2}}\frac{\partial y_{o2}}{\partial y_{i2}}\frac{\partial y_{i2}}{\partial w_{22}}\\ & =-(z-x)\cdot \frac{\partial x}{\partial u}\cdot v_{12}\cdot \frac{\partial y_{o2}}{\partial y_{i2}}\cdot x\end{array}\text{\hspace{1em}(14)}$$

$$\begin{array}{rl}\frac{\partial J}{\partial w_{31}}& =\frac{\partial J}{\partial x}\frac{\partial x}{\partial u}\frac{\partial u}{\partial y_{o3}}\frac{\partial y_{o3}}{\partial y_{i3}}\frac{\partial y_{i3}}{\partial w_{31}}\\ & =-(z-x)\cdot \frac{\partial x}{\partial u}\cdot v_{13}\cdot \frac{\partial y_{o3}}{\partial y_{i3}}\cdot z\end{array}\text{\hspace{1em}(15)}$$

其中

$$\frac{\partial y_{o3}}{\partial y_{i3}}=\frac{\Delta y_{o3}}{\Delta y_{i3}}=\frac{y_{o3}(k)-y_{o3}(k-1)}{y_{i3}(k)-y_{i3}(k-1)}=\frac{y_{o3}(k)-y_{o3}(k-1)}{y_{o3}(k)}$$

依旧使用符号函数归一化

$$\frac{\partial y_{o3}}{\partial y_{i3}}=\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\frac{y_{o3}(k)-y_{o3}(k-1)}{y_{o3}(k)}$$

同理

$$\begin{array}{rl}\frac{\partial J}{\partial w_{32}}& =\frac{\partial J}{\partial x}\frac{\partial x}{\partial u}\frac{\partial u}{\partial y_{o3}}\frac{\partial y_{o3}}{\partial y_{i3}}\frac{\partial y_{i3}}{\partial w_{32}}\\ & =-(z-x)\cdot \frac{\partial x}{\partial u}\cdot v_{13}\cdot \frac{\partial y_{o3}}{\partial y_{i3}}\cdot x\end{array}\text{\hspace{1em}(16)}$$

1.3 权值更新

如果使用传统的梯度下降法，则更新公式为

$$W=W-{\alpha }_1\frac{\partial J}{\partial W}\text{\hspace{1em}(17)}$$

$$V=V-{\alpha }_2\frac{\partial J}{\partial V}\text{\hspace{1em}(18)}$$

其中，${\alpha }_1,{\alpha }_2$为学习率。

有时，也增加动量项，则更新公式为

$$\begin{array}{rl}& W_d(k)={\beta }_1{W}_d(k-1)+(1-{\beta }_1)\frac{\partial J}{\partial W}\\ & W=W-{\alpha }_1{W}_d\end{array}\text{\hspace{1em}(19)}$$

$$\begin{array}{rl}& V_d(k)={\beta }_2{V}_d(k-1)+(1-{\beta }_2)\frac{\partial J}{\partial V}\\ & V=V-{\alpha }_2{V}_d\end{array}\text{\hspace{1em}(20)}$$

其中，${\beta }_1,{\beta }_2$为动量因子，一般取 0.9；$W_d,V_d$ 可取初始值为0进行迭代。

1.4 实际问题

以上算法纯属理论，在仿真中可能都会遇到问题。一个典型的问题是除数为0的情况，在这里很容易发生，例如 $u(k)=u(k-1)$ 就是如此。另一个问题是数值过大，比如除数很小就很容易导致这种现象。因此有必要规避除数为0，也要做好限幅工作。写程序时需要注意这些细节。

二、仿真

现假设受控系统是一个式(4) 描述的系统，设期望值为一个阶梯信号，整个程序如下

%% 参数初始化
% 初始化
rng(1);                         % 设置随机数种子
z = 1;                          % 目标值
x = 0;                          % 实际值初始化
W = 0.3*(rand(3,2) - 0.5);      % 隐含层—输入层权重矩阵
V = 0.3*(rand(3,1) - 0.5);      % 输出层—隐含层权重矩阵%学习率
alpha1 = 0.06;                  % W权重相关学习率
alpha2 = 0.02;                  % V权重相关学习率% 动量因子
beta1 = 0.9;
beta2 = 0.9;% 限幅值
xmax = 1;
ymax = 1;
umax = 1;% 变量初始化，_1 结尾为上一次的值，_2 结尾表示上两个时刻值
yi3_1 = 0;                      
u_1 = 0;
u_2 = 0;
x_1 = 0;
yi2_1 = 0;
yo3_1 = 0;
dW = 0;                         % W变化量，初始化为0
dV = 0;
yo = zeros(3,1);     xdata = [];                     % 记录实际值
zdata = [];                     % 记录期望值N = 2000;                       % 迭代次数
for k=1:N%% 设置目标值if k <500z = 0.5;elseif k < 1000z = 0.2;elseif k < 1500 z = 0.8;elsez = 0;end%% 正向传播% 隐含层输入yi = W * [z; x];                % 隐含层输出yo(1) = yi(1);                  % P  yo(2) = yo(2) + yi(2);          % Iyo(3) = yi(3) - yi3_1;          % Dyo(find(yo>ymax)) = ymax;       % 限幅yo(find(yo<-ymax)) = -ymax;% 输出层输出u = V' * yo;                    u(find(u>umax)) = umax;u(find(u<-umax)) = -umax;% 受控对象输出x = u^2 + 0.1*x_1;                  x(find(x>xmax)) = xmax;         x(find(x<-xmax)) = -xmax;% 损失函数J = 1/2 * (z-x)^2;              %% 反向传播% 计算J对V的偏导数 pJ_pVpJ_px = -(z-x);temp = u - u_1;                     % u(k)-u(k-1)if temp >= 0 && temp < 1e-20        % 除数限幅在(-∞,-1e-20]∪[1e-20,+∞)temp = 1e-20;                   % 防止除数为0elseif temp < 0 && temp > -1e-20temp = -1e-20;endpx_pu = sign((x - x_1) / temp);     % 使用sign，限幅在{-1,0,1}pJ_pV = pJ_px * px_pu * yo;         % 误差对V的偏导,yo为3x1向量% 计算J对W的偏导数 pJ_pWpJ_pw11 = pJ_px * px_pu * V(1) * 1 * z;pJ_pw12 = pJ_px * px_pu * V(1) * 1 * x;temp = yi(2) - yi2_1;               % yi(k) - yi(k-1)if temp >= 0 && temp < 1e-20        % 除数限幅在(-∞,-1e-20]∪[1e-20,+∞)temp = 1e-20;                   % 防止除数为0elseif temp < 0 && temp > -1e-20temp = -1e-20;endpJ_pw21 = pJ_px * px_pu * V(2) * (sign(yi(2)/temp)) * z;pJ_pw22 = pJ_px * px_pu * V(2) * (sign(yi(2)/temp)) * x;temp = yo(3) ;                      % yo(k)if temp >= 0 && temp < 1e-20        % 除数限幅在(-∞,-1e-20]∪[1e-20,+∞)temp = 1e-20;                   % 防止除数为0elseif temp < 0 && temp > -1e-20temp = -1e-20;endpJ_pw31 = pJ_px * px_pu * V(3) * (sign((yo(3) - yo3_1)/temp)) * z;pJ_pw32 = pJ_px * px_pu * V(3) * (sign((yo(3) - yo3_1)/temp)) * x;pJ_pW = [pJ_pw11, pJ_pw12; pJ_pw21, pJ_pw22; pJ_pw31, pJ_pw32]; % 误差对W的偏导%% 动量法权重更新dW = beta1 * dW + (1-beta1) * pJ_pW;        % 动量法计算增量dV = beta2 * dV + (1-beta2) * pJ_pV;W = W - alpha1 * dW;                        % 权重更新V = V - alpha2 * dV;%% 其他数据更新u_2 = u_1;u_1 = u;                                    % u(k-1)x_1 = x;                                    % x(k-1)yi2_1 = yi(2);                              % yi2_1 为上一次 yi(2)yo3_1 = yo(3);                              % yo3_1 为上一次 yo(3)xdata = [xdata; x];                         % 记录数据方便绘图zdata = [zdata; z];
end%% 可视化
plot(1:N, zdata, 'LineWidth',1.5);hold on;      % 目标值
plot(1:N, xdata, '.'); hold off                 % 实际值
legend('目标值','实际值')                        % 标注
title('PID神经网络');                           % 标题

运行结果如下

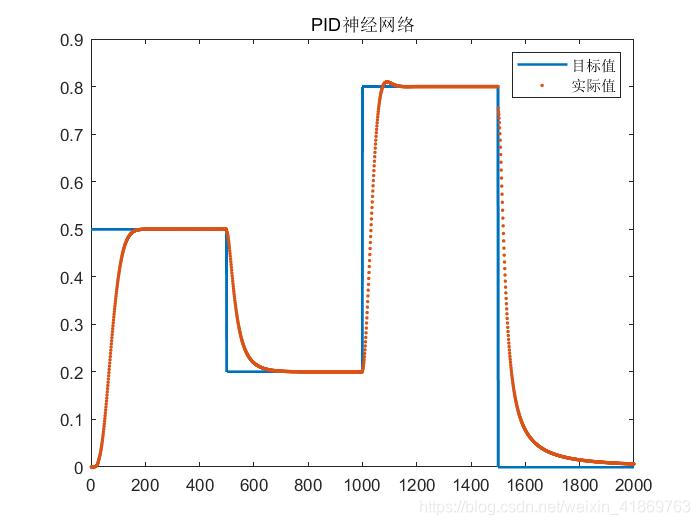
可见，跟踪效果很不错。不过，和所有神经网络一样，参数要小心谨慎，如果设置不合理，就达不到期望的效果。

四、总结与展望

和PID和神经网络相比，PID神经网络有什么美妙之处呢？其实，它结合了两者的优势，PID使用了反馈控制，好的PID参数使得实际值快速稳定地接近目标值，但是有时候很难调节出一组好的PID参数。神经网络的优势是，通过误差反馈传播调整权值，这个过程是自动完成的。PID参数已经通过权值的方式隐藏在网络结构中，使用反向传播时该参数自动得到优化。

其实，PID神经网络大显身手的地方是多输入多输出的耦合系统的控制，下一次，就用来做一个无人机姿态控制器。

— 完 —