本文主要是介绍【免费】两阶段鲁棒优化matlab实现——CCG和benders,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1 主要内容
2 部分代码
3 程序结果
4 下载链接
1 主要内容
程序采用matlab复现经典论文《Solving two-stage robust optimization problems using a column-and-constraint generation method》算例,实现了C&CG和benders算法两部分内容,通过对比学习能够方便掌握两种算法的编程要点,深入了解C&CG算法优势,对于学习鲁棒优化是不可多得的资料,程序均采用matlab+cplex求解!

2 部分代码
y = binvar(3,1);
z = sdpvar(3,1);
x =sdpvar(9,100,'full');
eta = sdpvar(1);
g = sdpvar(3,1);
pi = sdpvar(size(G,1),1);
v=binvar(size(G,1),1);
w=binvar(size(G,2),1);
%% CCG
LB=-inf; UB=inf; iter=1; BigM=1e5;
MP_Cons = [ 0<=z<=800*y, 772<=sum(z), b'*x(:,iter)<=eta, 0<=x(:,iter) ];
MP_Obj = coe1*y +coe2*z+eta ;
ops = sdpsettings('solver','cplex','verbose',0);
Uncertain_Cons=[ 0<=g<=1, sum(g)<=1.8, g(1)+g(2)<=1.2 ];
while abs(UB-LB) >1e-5disp(['迭代第',num2str(iter),'次'])optimize(MP_Cons,MP_Obj,ops);LB = max(LB, value(MP_Obj)); % LBSP_Obj = b'*x(:,iter) ;SP_Cons = [ Uncertain_Cons, 0<=x(:,iter), G*x(:,iter)>=h-E*[value(y);value(z)]-M*g ];SP_Cons = [SP_Cons, 0<=pi, G'*pi<=b ];SP_Cons = [SP_Cons, G*x(:,iter)-h+E*[value(y); value(z)]+M*g <= BigM*(1-v) ];SP_Cons = [SP_Cons, pi<=BigM*v];SP_Cons = [SP_Cons, b-G'*pi <= BigM*(1-w) ];SP_Cons = [SP_Cons, x(:,iter)<=BigM*w ]; sol_SP=optimize(SP_Cons,-SP_Obj,ops);if sol_SP.problem==0 % SP is solvedUB=min(UB, coe1*value(y)+coe2*value(z)+value(SP_Obj)); % UBdisp([' g = ',num2str(value(g)')]);endMP_Cons = [MP_Cons, 0<=x(:,iter+1), b'*x(:,iter+1)<= eta, G*x(:,iter+1)>=h- E*[y;z]-M*value(g) ];iter = iter+1;display([' LB: ',num2str(LB), ' UB: ',num2str(UB),]);
end
3 程序结果

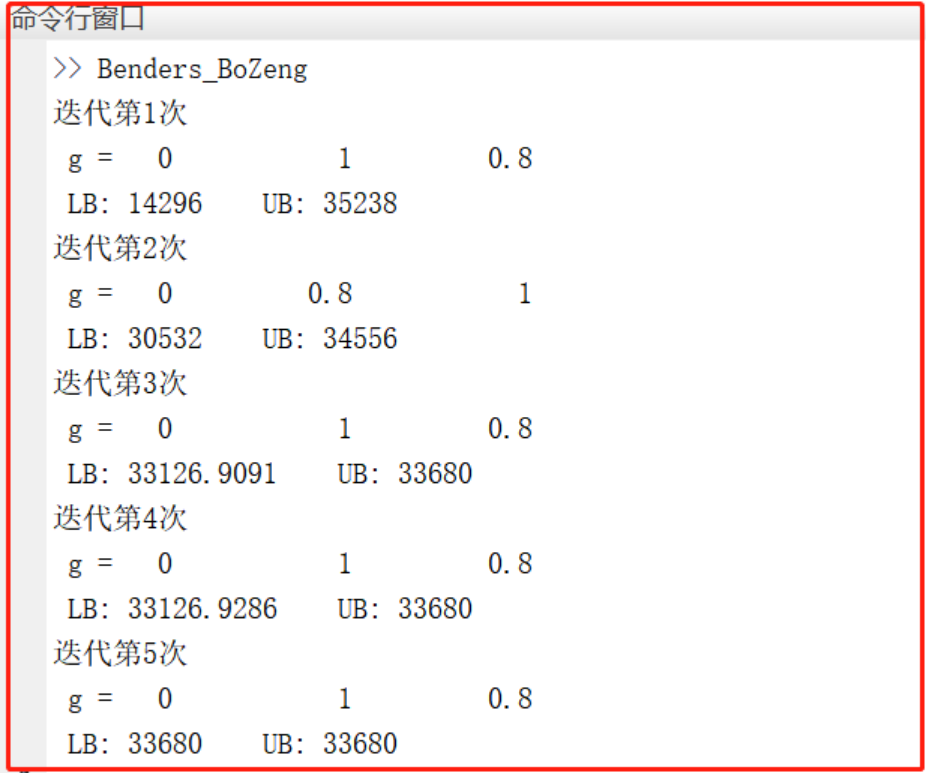
4 下载链接
这篇关于【免费】两阶段鲁棒优化matlab实现——CCG和benders的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






