数据结构13：哈夫曼树及编码

哈夫曼树

路径：从树中一个结点到另一个结点之间的分支构成这两个结点间的路径

结点的路径长度：两结点间路径上的分支数。

树的路径长度：从树根到每一个结点的路径长度之和。

结点树目相同的二叉树中，完全二叉树是路径长度最短的二叉树

权:将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权

1结点的带权路径长度：从根结点到该结点之间的路径长度与该结点的权的乘积

树的带权路径长度：树中所有叶子节点的带权路径长度之和。

哈夫曼编码

在哈夫曼树的每个分支上标上0或1：

1. 结点的左分支标0，右分支标。
2. 把从根到每个叶子的路径上的标号连接起来，作为该叶子代表的字符的编码。

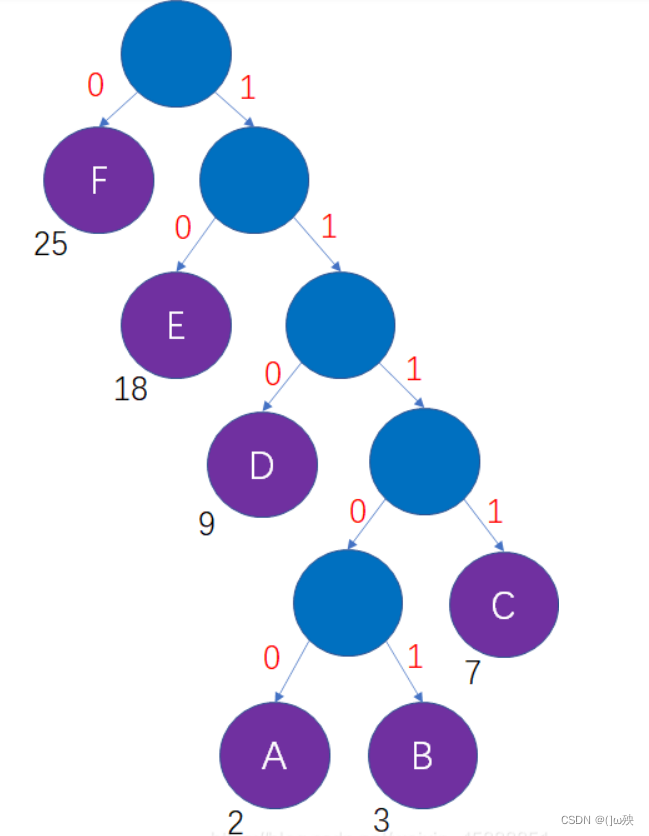
总代码

#include <stdio.h>
#include <stdlib.h>
#include <string.h>typedef double DataType; //结点权值的数据类型typedef struct HTNode //单个结点的信息
{DataType weight; //权值int parent; //父节点int lc, rc; //左右孩子
}*HuffmanTree;typedef char **HuffmanCode; //字符指针数组中存储的元素类型//在下标为1到i-1的范围找到权值最小的两个值的下标，其中s1的权值小于s2的权值
void Select(HuffmanTree& HT, int n, int& s1, int& s2)
{int min;//找第一个最小值for (int i = 1; i <= n; i++){if (HT[i].parent == 0){min = i;break;}}for (int i = min + 1; i <= n; i++){if (HT[i].parent == 0 && HT[i].weight < HT[min].weight)min = i;}s1 = min; //第一个最小值给s1//找第二个最小值for (int i = 1; i <= n; i++){if (HT[i].parent == 0 && i != s1){min = i;break;}}for (int i = min + 1; i <= n; i++){if (HT[i].parent == 0 && HT[i].weight < HT[min].weight&&i != s1)min = i;}s2 = min; //第二个最小值给s2
}//构建哈夫曼树
void CreateHuff(HuffmanTree& HT, DataType* w, int n)
{int m = 2 * n - 1; //哈夫曼树总结点数HT = (HuffmanTree)calloc(m + 1, sizeof(HTNode)); //开m+1个HTNode，因为下标为0的HTNode不存储数据for (int i = 1; i <= n; i++){HT[i].weight = w[i - 1]; //赋权值给n个叶子结点}for (int i = n + 1; i <= m; i++) //构建哈夫曼树{//选择权值最小的s1和s2，生成它们的父结点int s1, s2;Select(HT, i - 1, s1, s2); //在下标为1到i-1的范围找到权值最小的两个值的下标，其中s1的权值小于s2的权值HT[i].weight = HT[s1].weight + HT[s2].weight; //i的权重是s1和s2的权重之和HT[s1].parent = i; //s1的父亲是iHT[s2].parent = i; //s2的父亲是iHT[i].lc = s1; //左孩子是s1HT[i].rc = s2; //右孩子是s2}//打印哈夫曼树中各结点之间的关系printf("哈夫曼树为:>\n");printf("下标   权值     父结点   左孩子   右孩子\n");printf("0                                  \n");for (int i = 1; i <= m; i++){printf("%-4d   %-6.2lf   %-6d   %-6d   %-6d\n", i, HT[i].weight, HT[i].parent, HT[i].lc, HT[i].rc);}printf("\n");
}//生成哈夫曼编码
void HuffCoding(HuffmanTree& HT, HuffmanCode& HC, int n)
{HC = (HuffmanCode)malloc(sizeof(char*)*(n + 1)); //开n+1个空间，因为下标为0的空间不用char* code = (char*)malloc(sizeof(char)*n); //辅助空间，编码最长为n(最长时，前n-1个用于存储数据，最后1个用于存放'\0')code[n - 1] = '\0'; //辅助空间最后一个位置为'\0'for (int i = 1; i <= n; i++){int start = n - 1; //每次生成数据的哈夫曼编码之前，先将start指针指向'\0'int c = i; //正在进行的第i个数据的编码int p = HT[c].parent; //找到该数据的父结点while (p) //直到父结点为0，即父结点为根结点时，停止{if (HT[p].lc == c) //如果该结点是其父结点的左孩子，则编码为0，否则为1code[--start] = '0';elsecode[--start] = '1';c = p; //继续往上进行编码p = HT[c].parent; //c的父结点}HC[i] = (char*)malloc(sizeof(char)*(n - start)); //开辟用于存储编码的内存空间strcpy(HC[i], &code[start]); //将编码拷贝到字符指针数组中的相应位置}free(code); //释放辅助空间
}//主函数
int main()
{int n = 0;printf("请输入数据个数:");scanf("%d", &n);DataType* w = (DataType*)malloc(sizeof(DataType)*n);if (w == NULL){printf("malloc fail\n");exit(-1);}printf("请输入数据:");for (int i = 0; i < n; i++){scanf("%lf", &w[i]);}HuffmanTree HT;CreateHuff(HT, w, n); //构建哈夫曼树HuffmanCode HC;HuffCoding(HT, HC, n); //构建哈夫曼编码for (int i = 1; i <= n; i++) //打印哈夫曼编码{printf("数据%.2lf的编码为:%s\n", HT[i].weight, HC[i]);}free(w);return 0;
}

运行结果

请输入数据个数:6
请输入数据:2 3 7 9 18 25
哈夫曼树为:>
下标   权值     父结点   左孩子   右孩子
0
1      2.00     7        0        0
2      3.00     7        0        0
3      7.00     8        0        0
4      9.00     9        0        0
5      18.00    10       0        0
6      25.00    11       0        0
7      5.00     8        1        2
8      12.00    9        7        3
9      21.00    10       4        8
10     39.00    11       5        9
11     64.00    0        6        10数据2.00的编码为:11100
数据3.00的编码为:11101
数据7.00的编码为:1111
数据9.00的编码为:110
数据18.00的编码为:10
数据25.00的编码为:0