数据结构C++——哈夫曼树及哈夫曼编码

2024-02-29 03:30
文章标签 c++ 数据结构 编码 哈夫曼 树及

本文主要是介绍数据结构C++——哈夫曼树及哈夫曼编码，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

数据结构C++——哈夫曼树及哈夫曼编码

文章目录

  • 数据结构C++——哈夫曼树及哈夫曼编码
    • 一、哈夫曼树的介绍及概念
    • 二、哈夫曼树的构造及打印
      • ①哈夫曼树的存储结构
      • ②构造哈夫曼树
      • ③Select()函数的代码实现
      • ④打印哈夫曼树
      • ⑤测试的完整代码
    • 二、哈夫曼编码
      • ①哈夫曼编码的相关概念
      • ②哈夫曼编码的算法实现
      • ③输出哈夫曼编码
      • ④测试的完整代码
    • 三、总结

一、哈夫曼树的介绍及概念

哈夫曼(Huffman)树又称最优树，是一类带权路径长度最短的树，在实际中有广泛的用途。
(1) 路径：从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径。
(2) 路径长度：路径上的分支数目称作路径长度。
(3)树的路径长度：从树根到每一结点的路径长度之和。
(4)权：赋予某个实体的一个量，是对实体的某个或某些属性的数值化描述。 在数据结构中，实体有结点（元素）和边（关系）两大类，所以对应有结点权和边权。 结点权或边权具体代表什么意义，由具体情况决定。如果在一棵树中的结点上带有权值，则对应的就有带权树等概念。
(5)结点的带权路径长度：从该结点到树根之间的路径长度与结点上权的乘积。
(6)树的带权路径长度：树中所有叶子结点的带权路径长度之和。
(7)哈夫曼树：假设有m个权值{w1, W2, …，匹}，可以构造一棵含n个叶子结点的二叉树，每个叶子结点的权为 W; 则其中带权路径长度 WPL最小的二叉树称做最优二叉树或哈夫曼树

二、哈夫曼树的构造及打印

①哈夫曼树的存储结构

哈夫曼树的存储结构

typedef struct {int weight;//结点的权值int parent, lchild, rchild;//结点的双亲、左孩子、右孩子的下标
}HTNode,*HuffmanTree;//动态分配数组存储哈夫曼树

②构造哈夫曼树

构造哈夫曼树

构造哈夫曼树的算法思路：
1：定义哈夫曼树变量，申请2*n个单元（0号单元未用），HT[2*n-1]表示根结点
2：定义变量m=2*n-1（一棵有n个叶子结点的哈夫曼树共有2*n-1个结点），循环m次，将1~m号中的的双亲、左孩子、右孩子、权重的下标都初始化为0
3：输入前n个单元中叶子结点的权值
4：在前n个单元中找到权值最小且双亲结点下标为0的结点，并返回它们在HT中的序号s1和s2
5：将s1和s2的双亲域由0改为i，s1和s2分别作为HT[i]的左右孩子，并修改HT[i]的权值为左右孩子的权值之和。

void CreateHuffmanTree(HuffmanTree& HT, int n) {//构造哈夫曼树if (n <= 1)return;int m = 2 * n - 1;//一棵有n个叶子节点的哈夫曼树共有2*n-1个结点HT = new HTNode[m + 1];//0号单元未用，所以需要动态分配m+1个单元，HT[m]表示根结点for (int i = 1; i <= m; i++){//将1-m号单元中的双亲、左孩子、右孩子的下标都初始化为0HT[i].parent = 0;HT[i].lchild = 0;HT[i].rchild = 0;HT[i].weight = 0;}for (int i = 1; i <= n; i++) {//输入前n个单元中叶子结点的权值cin >> HT[i].weight;}/*--------初始化工作结束，下面开始创建哈夫曼树------*/for (int i = n+1; i <= m; i++){//通过n-1次的选择、删除、合并来创建哈夫曼树int s1=0, s2=0;Select(HT, i - 1, s1, s2);//在HT[k](1<=k<=i-1)中选择两个其双亲域为0且权值最小的结点，并返回它们在HT中的序号s1和s2HT[s1].parent = i; HT[s2].parent = i;//得到新结点i，从森林中删除s1,s2，将s1和s2的双亲域由0改为iHT[i].lchild = s1; HT[i].rchild = s2;//s1，s2分别作为i的左右孩子HT[i].weight = HT[s1].weight + HT[s2].weight;//i的权值为左右孩子权值之和}
}

③Select()函数的代码实现

Select()函数的实现
此步骤参照了此文章，即本步骤并非笔者纯原创：数据结构(15)–哈夫曼树以及哈夫曼编码的实现.

Select()函数代码实现思路：
1：设置中间变量tmp存放最小权值结点的权值
2：循环n次，找到权值最小的结点下标，将其赋予s1
3：重复第2步，找到权值最小但下标不为s1的结点下标，将其赋予s2

/*----------选择两个权值最小的结点-----------*/
void Select(HuffmanTree HT, int k, int& s1, int& s2) {unsigned int tmp = 10000;//假设s1对应的权值大于s2for (int i = 1; i <= k; i++){if (!HT[i].parent){//parent必须为0if (tmp>HT[i].weight){tmp = HT[i].weight;//tmp存放权值最小的结点权值s1 = i;}}}unsigned int tmp1 = 10000;//假设s1对应的权值大于s2for (int i = 1; i <= k; i++){if (!HT[i].parent&&i!=s1){//parent必须为0if (tmp1 > HT[i].weight){tmp1 = HT[i].weight;//tmp1存放权值最小的结点权值s2 = i;}}}
}

④打印哈夫曼树

打印哈夫曼树

打印哈夫曼树的算法思路：
1：将哈夫曼树以表格的形式输出更直观
2：输出表头i、weight、parent、lchild、rchild。
3：输出时注意C++函setw()的使用，注意左对齐为在setw()函数中加上std::left，右对齐则加上std::right。
4：循环2*n-1次输出构造好的哈夫曼树的每个结点的相关参数。

/*----------打印哈夫曼树---------*/
void PrintHuffmanTree(HuffmanTree HT,int m) {cout <<std::left << setw(10) << "i" << setw(10) << "weight" << setw(10) << "parent" << setw(10) << "lchild" << setw(10) << "rchild" << endl;for (int i = 1; i <= m; i++){cout << setw(12) << i << setw(11) << HT[i].weight << setw(10) << HT[i].parent << setw(10) << HT[i].lchild << setw(10) << HT[i].rchild << endl;}
}

⑤测试的完整代码

完整代码

#include<iostream>
#include<iomanip>
using namespace std;
typedef struct {int weight;//结点的权值int parent, lchild, rchild;//结点的双亲、左孩子、右孩子的下标
}HTNode,*HuffmanTree;//动态分配数组存储哈夫曼树
/*----------选择两个权值最小的结点-----------*/
void Select(HuffmanTree HT, int k, int& s1, int& s2) {unsigned int tmp = 10000;//假设s1对应的权值大于s2for (int i = 1; i <= k; i++){if (!HT[i].parent){//parent必须为0if (tmp>HT[i].weight){tmp = HT[i].weight;//tmp存放权值最小的结点权值s1 = i;}}}unsigned int tmp1 = 10000;//假设s1对应的权值大于s2for (int i = 1; i <= k; i++){if (!HT[i].parent&&i!=s1){//parent必须为0if (tmp1 > HT[i].weight){tmp1 = HT[i].weight;//tmp1存放权值最小的结点权值s2 = i;}}}
}
/*-------构造哈夫曼树-------*/
void CreateHuffmanTree(HuffmanTree& HT, int n) {//构造哈夫曼树if (n <= 1)return;int m = 2 * n - 1;//一棵有n个叶子节点的哈夫曼树共有2*n-1个结点HT = new HTNode[m + 1];//0号单元未用，所以需要动态分配m+1个单元，HT[m]表示根结点for (int i = 1; i <= m; i++){//将1-m号单元中的双亲、左孩子、右孩子的下标都初始化为0HT[i].parent = 0;HT[i].lchild = 0;HT[i].rchild = 0;HT[i].weight = 0;}for (int i = 1; i <= n; i++) {//输入前n个单元中叶子结点的权值cin >> HT[i].weight;}/*--------初始化工作结束，下面开始创建哈夫曼树------*/for (int i = n+1; i <= m; i++){//通过n-1次的选择、删除、合并来创建哈夫曼树int s1=0, s2=0;Select(HT, i - 1, s1, s2);//在HT[k](1<=k<=i-1)中选择两个其双亲域为0且权值最小的结点，并返回它们在HT中的序号s1和s2HT[s1].parent = i; HT[s2].parent = i;//得到新结点i，从森林中删除s1,s2，将s1和s2的双亲域由0改为iHT[i].lchild = s1; HT[i].rchild = s2;//s1，s2分别作为i的左右孩子HT[i].weight = HT[s1].weight + HT[s2].weight;//i的权值为左右孩子权值之和}
}
/*----------打印哈夫曼树---------*/
void PrintHuffmanTree(HuffmanTree HT,int m) {cout <<std::left << setw(10) << "i" << setw(10) << "weight" << setw(10) << "parent" << setw(10) << "lchild" << setw(10) << "rchild" << endl;for (int i = 1; i <= m; i++){cout << setw(12) << i << setw(11) << HT[i].weight << setw(10) << HT[i].parent << setw(10) << HT[i].lchild << setw(10) << HT[i].rchild << endl;}
}
/*--------主函数--------*/
int main() {HuffmanTree HT = new HTNode;//定义一个哈夫曼树变量int n=0;cin >> n;//输入结点个数int m = 2 * n - 1;//m为哈夫曼树的所有结点的个数CreateHuffmanTree(HT, n);//构建一个哈夫曼树PrintHuffmanTree(HT, m);//输出哈夫曼树
}
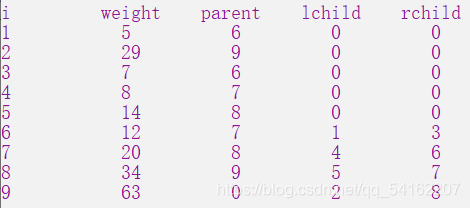
//5 29 7 8 14

测试结果

输入：55 29 7 8 14

输出结果

输出：

在这里插入图片描述
--------------------------------一道华丽的分割线-----------------------------------

二、哈夫曼编码

①哈夫曼编码的相关概念

(l)前缀编码：如果在一个编码方案中，任一个编码都不是其他任何编码的前缀（最左子串），则称编码是前缀编码。例如：0，10，110，111是前缀编码，而0，01，010，111就不是前缀编码，前缀编码可以保证对压缩文件进行解码时不产生二义性， 确保正确解码。
(2) 哈夫曼编码：对一棵具有n个叶子的哈夫曼树，若对树中的每个左分支赋予0, 右分支赋予1’则从根到每个叶子的路径上，各分支的赋值分别构成一个二进制串， 该二进制串就称为哈夫曼编码。

②哈夫曼编码的算法实现

算法思路

在构造哈夫曼树之后，求哈夫曼编码的主要思想是：依次以叶子为出发点，向上回溯至根结
点为止。 回溯时走左分支则生成代码 0, 走右分支则生成代码l。

哈夫曼编码表的存储表示

/*----------哈夫曼编码表的存储表示------------*/
typedef char** HuffmanCode;//动态分配数组存储哈夫曼编码表

根据哈夫曼树求哈夫曼编码

根据哈夫曼树求哈夫曼编码的算法思路：
1：定义HC指针数组，数组的每一个单元存储一个指针，定义cd数组，临时存储每一个叶子结点的字符编码
2：遍历n个叶子结点，从叶子结点开始向上回溯，直到根结点
3：若c为回溯到的父结点的左子树的根结点，则生成代码0
4：若c为回溯到的父结点的右子树的根结点，则生成代码1
5：回溯一次start向前指一个位置，最后cd数组中实际存值的单元为start~n-1这段单元
6：最后将求得的编码从临时空间cd复制到HC的当前行中

/*---------根据哈夫曼树求哈夫曼编码------------*/
void CreatHuffmanCode(HuffmanTree HT, HuffmanCode& HC, int n) {//从叶子到根逆向求每个字符的哈夫曼编码，存储在编码表HC中HC = new char* [n + 1];//分配存储n个字符编码的编码表空间char* cd = new char[n];//分配临时存放每个字符编码的动态数组空间cd[n - 1] = '\0';//编码结束符for (int i = 1; i <= n; i++) {int start = n - 1;//start开始时指向最后，即编码结束符位置int c = 0 , f = 0;c = i; f = HT[i].parent;//f指向结点c的双亲结点while (f!=0)//从叶子结点开始向上回溯，直到根结点{--start;//回溯一次start向前指一个位置if (HT[f].lchild == c) cd[start] = '0';//结点c是f的左孩子，则生成代码0else cd[start] = '1';//结点c是f的右孩子，则生成代码1c = f; f = HT[f].parent;//继续向上回溯}//求出第i个字符的编码HC[i] = new char[n - start];strcpy(HC[i], &cd[start]);//将求得的编码从临时空间cd复制到HC的当前行中}delete cd;//释放临时空间
}

③输出哈夫曼编码

将哈夫曼编码的结果输出在控制台

输出哈夫曼编码的算法思路：
1：输出表头
2：循环n次将HC数组中的内容输出

/*--------输出哈夫曼编码-----------*/
void PrintfHuffmanCode(HuffmanCode& HC, int n) {//将哈夫曼编码的结果输出在控制台cout << std::left << setw(10) << "i" << std::left << setw(10) << "编码" << endl;for (int i = 1; i <= n; i++) {cout << std::left << setw(10) << i;string str = HC[i];cout << std::left << setw(10) << str << endl;}
}

④测试的完整代码

#include<iostream>
#include<iomanip>
#include<string>
using namespace std;
/*----------哈夫曼编码表的存储表示------------*/
typedef char** HuffmanCode;//动态分配数组存储哈夫曼编码表
typedef struct {int weight;//结点的权值int parent, lchild, rchild;//结点的双亲、左孩子、右孩子的下标
}HTNode,*HuffmanTree;//动态分配数组存储哈夫曼树
/*----------选择两个权值最小的结点-----------*/
void Select(HuffmanTree HT, int k, int& s1, int& s2) {unsigned int tmp = 10000;//假设s1对应的权值大于s2for (int i = 1; i <= k; i++){if (!HT[i].parent){//parent必须为0if (tmp>HT[i].weight){tmp = HT[i].weight;//tmp存放权值最小的结点权值s1 = i;}}}unsigned int tmp1 = 10000;//假设s1对应的权值大于s2for (int i = 1; i <= k; i++){if (!HT[i].parent&&i!=s1){//parent必须为0if (tmp1 > HT[i].weight){tmp1 = HT[i].weight;//tmp1存放权值最小的结点权值s2 = i;}}}
}
/*-------构造哈夫曼树-------*/
void CreateHuffmanTree(HuffmanTree& HT, int n) {//构造哈夫曼树if (n <= 1)return;int m = 2 * n - 1;//一棵有n个叶子节点的哈夫曼树共有2*n-1个结点HT = new HTNode[m + 1];//0号单元未用，所以需要动态分配m+1个单元，HT[m]表示根结点for (int i = 1; i <= m; i++){//将1-m号单元中的双亲、左孩子、右孩子的下标都初始化为0HT[i].parent = 0;HT[i].lchild = 0;HT[i].rchild = 0;HT[i].weight = 0;}for (int i = 1; i <= n; i++) {//输入前n个单元中叶子结点的权值cin >> HT[i].weight;}/*--------初始化工作结束，下面开始创建哈夫曼树------*/for (int i = n+1; i <= m; i++){//通过n-1次的选择、删除、合并来创建哈夫曼树int s1=0, s2=0;Select(HT, i - 1, s1, s2);//在HT[k](1<=k<=i-1)中选择两个其双亲域为0且权值最小的结点，并返回它们在HT中的序号s1和s2HT[s1].parent = i; HT[s2].parent = i;//得到新结点i，从森林中删除s1,s2，将s1和s2的双亲域由0改为iHT[i].lchild = s1; HT[i].rchild = s2;//s1，s2分别作为i的左右孩子HT[i].weight = HT[s1].weight + HT[s2].weight;//i的权值为左右孩子权值之和}
}
/*---------根据哈夫曼树求哈夫曼编码------------*/
void CreatHuffmanCode(HuffmanTree HT, HuffmanCode& HC, int n) {//从叶子到根逆向求每个字符的哈夫曼编码，存储在编码表HC中HC = new char* [n + 1];//分配存储n个字符编码的编码表空间char* cd = new char[n];//分配临时存放每个字符编码的动态数组空间cd[n - 1] = '\0';//编码结束符for (int i = 1; i <= n; i++) {int start = n - 1;//start开始时指向最后，即编码结束符位置int c = 0 , f = 0;c = i; f = HT[i].parent;//f指向结点c的双亲结点while (f!=0)//从叶子结点开始向上回溯，直到根结点{--start;//回溯一次start向前指一个位置if (HT[f].lchild == c) cd[start] = '0';//结点c是f的左孩子，则生成代码0else cd[start] = '1';//结点c是f的右孩子，则生成代码1c = f; f = HT[f].parent;//继续向上回溯}//求出第i个字符的编码HC[i] = new char[n - start];strcpy(HC[i], &cd[start]);//将求得的编码从临时空间cd复制到HC的当前行中}delete cd;//释放临时空间
}
/*--------将哈夫曼编码的结果输出在控制台-----------*/
void PrintfHuffmanCode(HuffmanCode& HC, int n) {//将哈夫曼编码的结果输出在控制台//char* cd = new char[n];cout << std::left << setw(10) << "i" << std::left << setw(10) << "编码" << endl;for (int i = 1; i <= n; i++) {cout << std::left << setw(10) << i;string str = HC[i];cout << std::left << setw(10) << str << endl;}
}
/*--------主函数--------*/
int main() {HuffmanTree HT = new HTNode;//定义一个哈夫曼树变量int n=0;cin >> n;//输入结点个数int m = 2 * n - 1;//m为哈夫曼树的所有结点的个数CreateHuffmanTree(HT, n);//构建一个哈夫曼树//PrintHuffmanTree(HT, m);//输出哈夫曼树HuffmanCode HC;CreatHuffmanCode(HT, HC, n);PrintfHuffmanCode(HC, n);return 0;
}

输出结果

输入：
8
5 29 7 8 14 23 3 11

输出：

在这里插入图片描述

三、总结

以上为笔者对于哈夫曼树及哈夫曼编码的一些见解，希望初学者都能有所收获，有技术不到位的地方，还望各位大佬指正。
同时，笔者的个人主页还有数据结构中其他部分的一些见解与分析，后续数据结构的相关知识还将陆续更新，欢迎大家访问且共同学习！

这篇关于数据结构C++——哈夫曼树及哈夫曼编码的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/757443。

相关文章

基于Go语言实现Base62编码的三种方式以及对比分析

基于Go语言实现Base62编码的三种方式以及对比分析

《基于Go语言实现Base62编码的三种方式以及对比分析》Base62编码是一种在字符编码中使用62个字符的编码方式,在计算机科学中,,Go语言是一种静态类型、编译型语言,它由Google开发并开源,... 目录一、标准库现状与解决方案1. 标准库对比表2. 解决方案完整实现代码（含边界处理）二、关键实现细
阅读更多...
C++类和对象之初始化列表的使用方式

C++类和对象之初始化列表的使用方式

《C++类和对象之初始化列表的使用方式》：本文主要介绍C++类和对象之初始化列表的使用方式,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录C++初始化列表详解：性能优化与正确实践什么是初始化列表？初始化列表的三大核心作用1. 性能优化：避免不必要的赋值操作2. 强
阅读更多...
C++迭代器失效的避坑指南

C++迭代器失效的避坑指南

《C++迭代器失效的避坑指南》在C++中,迭代器（iterator）是一种类似指针的对象,用于遍历STL容器（如vector、list、map等）,迭代器失效是指在对容器进行某些操作后... 目录1. 什么是迭代器失效？2. 哪些操作会导致迭代器失效？2.1 vector 的插入操作（push_back,
阅读更多...
解决IDEA报错:编码GBK的不可映射字符问题

解决IDEA报错:编码GBK的不可映射字符问题

《解决IDEA报错:编码GBK的不可映射字符问题》：本文主要介绍解决IDEA报错:编码GBK的不可映射字符问题,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录IDEA报错:编码GBK的不可映射字符终端软件问题描述原因分析解决方案方法1：将命令改为方法2：右下jav
阅读更多...
C#如何调用C++库

C#如何调用C++库

《C#如何调用C++库》：本文主要介绍C#如何调用C++库方式,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录方法一：使用P/Invoke1. 导出C++函数2. 定义P/Invoke签名3. 调用C++函数方法二：使用C++/CLI作为桥接1. 创建C++/CL
阅读更多...
C++如何通过Qt反射机制实现数据类序列化

C++如何通过Qt反射机制实现数据类序列化

《C++如何通过Qt反射机制实现数据类序列化》在C++工程中经常需要使用数据类,并对数据类进行存储、打印、调试等操作,所以本文就来聊聊C++如何通过Qt反射机制实现数据类序列化吧... 目录设计预期设计思路代码实现使用方法在 C++ 工程中经常需要使用数据类，并对数据类进行存储、打印、调试等操作。由于数据类
阅读更多...
Linux下如何使用C++获取硬件信息

Linux下如何使用C++获取硬件信息

《Linux下如何使用C++获取硬件信息》这篇文章主要为大家详细介绍了如何使用C++实现获取CPU,主板,磁盘,BIOS信息等硬件信息,文中的示例代码讲解详细,感兴趣的小伙伴可以了解下... 目录方法获取CPU信息：读取"/proc/cpuinfo"文件获取磁盘信息：读取"/proc/diskstats"文
阅读更多...
C++使用printf语句实现进制转换的示例代码

C++使用printf语句实现进制转换的示例代码

《C++使用printf语句实现进制转换的示例代码》在C语言中,printf函数可以直接实现部分进制转换功能,通过格式说明符（formatspecifier）快速输出不同进制的数值,下面给大家分享C+... 目录一、printf 原生支持的进制转换1. 十进制、八进制、十六进制转换2. 显示进制前缀3. 指
阅读更多...
C++中初始化二维数组的几种常见方法

C++中初始化二维数组的几种常见方法

《C++中初始化二维数组的几种常见方法》本文详细介绍了在C++中初始化二维数组的不同方式,包括静态初始化、循环、全部为零、部分初始化、std::array和std::vector,以及std::vec... 目录1. 静态初始化2. 使用循环初始化3. 全部初始化为零4. 部分初始化5. 使用 std::a
阅读更多...
C++ vector的常见用法超详细讲解

C++ vector的常见用法超详细讲解

《C++vector的常见用法超详细讲解》：本文主要介绍C++vector的常见用法,包括C++中vector容器的定义、初始化方法、访问元素、常用函数及其时间复杂度,通过代码介绍的非常详细,... 目录1、vector的定义2、vector常用初始化方法1、使编程用花括号直接赋值2、使用圆括号赋值3、ve
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2