本文主要是介绍海明码的本质,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
海明码的实质,就是类似于一种二分性质的问答,每一次问答可以排除掉一半的可能,就像别人问你几个问题(均是类似“是男的吗?”这种yes or no 的问题)来猜你心中想的人。
具体通过一个例子来说明,现在我们有16个位置来传输海明码(包括信息码和校验码),我们为这16个从0-15位置编号,并将编号的位置作为校验码(原因在后面会体现出来),这里是1,2,4,8。

现在我们将1处放的值作为如图黄色两列的偶校验码,将2处放的值作为如图绿色两列的偶校验码。
然后,当我们对接受到的数据的黄色两列做偶校验,如果出错(假设只有一位错误),说明错误在黄色两列,此时如果绿色列也出错,那么就可以确定错误一定在最后一列。而1、2两个出错情况有四种组合(错错、错对、对错、对对),据此就可以确定错误在哪一列。
对于编号4、8处同理,可以错误确定在哪一行。
结合行和列就可以确定是哪一位数据出了错。

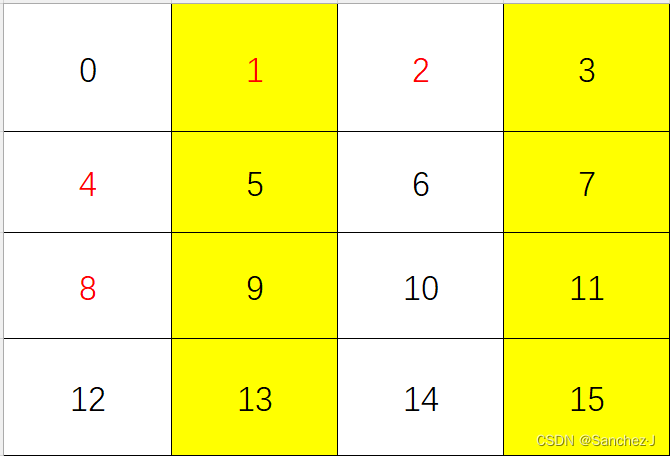
而实际上,我们将4个偶校验结果的值排列,比如0111(1、2、4处偶校验查出问题,8处偶校验没问题) ,这说明出错的位置影响到了1、2、4,没影响到8,可以确定是7处的数据错误。而
这并不是巧合, 把二进制下的编号列出来,我们会发现,问错误是不是发生在黄色列,就等价于在问错误的编号的二进制最后一位是不是1。也就是说,如果确定了错误在黄色列,就确定了错误的二进制编号的最后一位是1。
而其他几个校验对应的就是剩下的3位,这就解释了为什么偶校验结果组成的二进制串转化成十进制正好就是错误的位置。

现在,我们只需要对4个校验位分别做偶校验,然后将结果排列起来,就可以确定错误的地方。
这里我们会发现一个细节上的问题,如果四个偶校验都没问题(结果都是0),那么是说明0号位出错还是说明没错呢?
再深入想,这里的问题本质上其实是:检查错误的结果有种,但实际上有17种情况(16个位置其中一个发生错误或者没有错) 。我们没有考虑到如果没出错应该怎么表示。
一个简单的方法是直接将0号位剔除,不做信息位,这样校验结果为0时就说明没有错误,这也就是为什么在海明码中编号从1开始。
在扩展海明码中,这个0号位被巧妙地利用起来,用来做整体的偶校验位,这样,海明码不仅能纠正1位错,还能查两位错。
懂了上面的过程,我们就无需去死记硬背,下面再结合Logisim实验设计看一下更一般的情况。
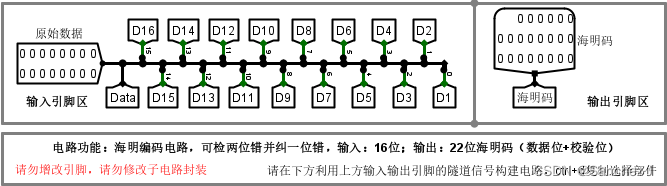
这里原始数据有16位,而根据上面的讨论可以发现,原始数据位+校验位(n + 1位)要比某个2的n次幂小,这里容易得出n = 5。
于是可以做出图来:(P是校验位,D是数据位)


注意这里左右两个实际上是叠在一起的(和5阶卡诺图中类似) ,当P1处检查出错误时,实际上说明错误在左图1、3列和右图1、3列一共四列中,这一点结合二分就很好理解,每一个校验位将错误范围减半,这里要减半就是限制在4列而不是2列。
根据图可以轻松得到:
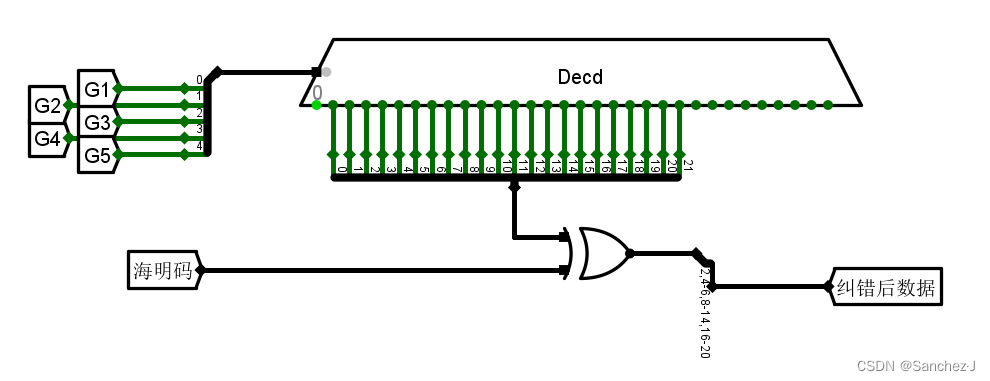
而解码就和偶校验一样的得到校验结果到
,然后就可以判断错误个数。
纠正错误可以如下用译码器进行,注意下标从1开始在这里的体现。
这篇关于海明码的本质的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!