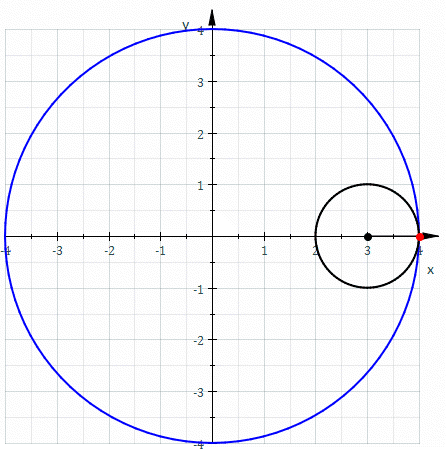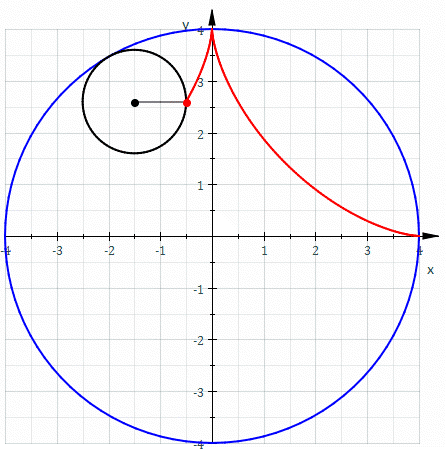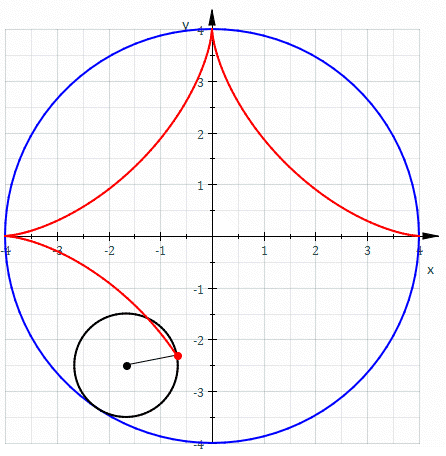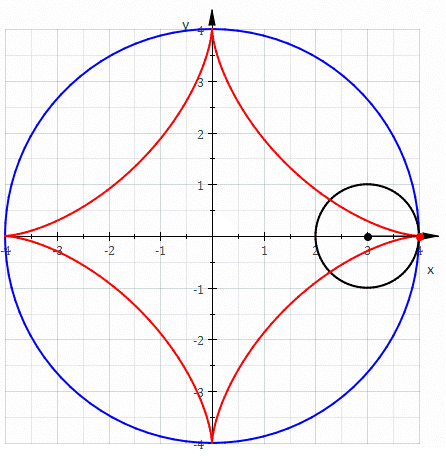
典型参数方程曲线@摆线@星形线

旋轮线

• ggb在线绘图
• refs:摆线 (wikipedia.org)

摆线

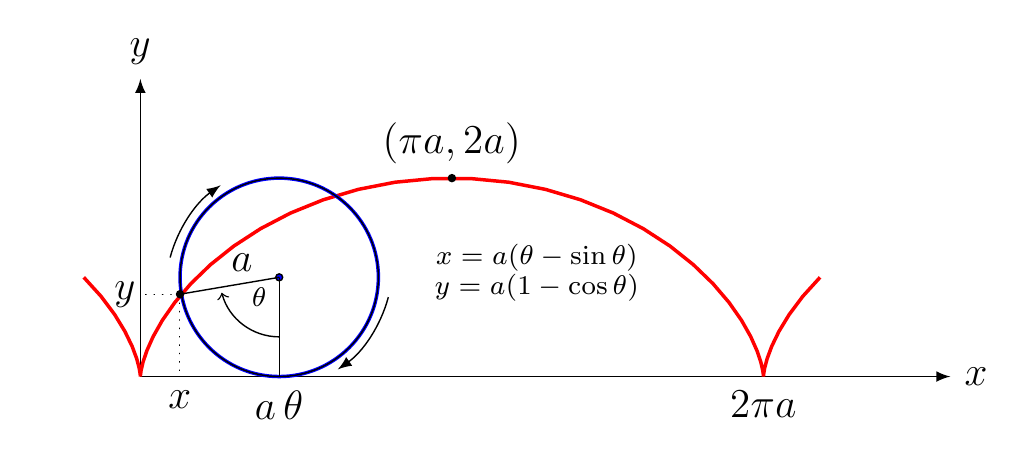
• 在数学中，摆线（Cycloid）被定义为，一个圆在一条直线上滚动时，圆边界上一定点所形成的轨迹。
  • 它是一般旋轮线的一种。摆线亦称圆滚线。
  • 摆线也是最速降线问题和等时降落问题的解。

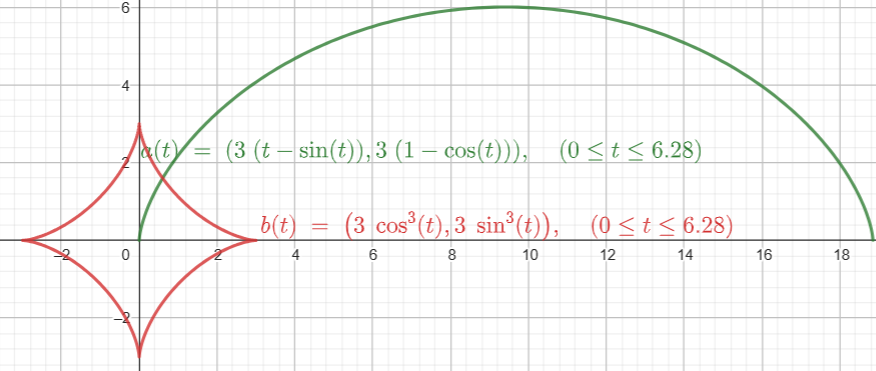性质

• 它的长度等于旋转圆直径的 4 倍。它的长度是 一个不依赖于π的有理数。
• 在弧线下的面积，是旋转圆面积的三倍。
• 圆上描出摆线的那个点，具有不同的速度——事实上，在特定的地方它甚至是静止的。
• 当弹子从一个摆线形状的容器的不同点放开时，它们会同时到达底部。

方程推导

• 在半径为$r$的圆,从圆心$C$在$y$轴上的$C(0,a)$,取此时圆周上的点$A_0(0,0)$作为观察点,$y$轴和初始位置圆的另一交点为$B_0(0,2a)$,在圆上分别标记这两点,在随着圆周滚动的过程中,圆心始终处于$y=a$这一直线上

• 容易确定最高点的纵坐标为$2a$;而圆的边缘和$x$轴接触过的部分恰好是半个圆周,即$\pi r$,此时$B_0$点位于$(\pi r,0)$,$A_0$位于摆线最高点$(\pi r,2a)$

• 取摆线上的任一位置$A(x,y)$将其和圆心$C^{\prime }$连线,并作$C^{\prime }Q\perp x$,$C^{\prime }Q$交$x$轴与$Q$点,

  • 令$t=\angle Q{C}^{\prime }A$

  • 显然$t:0\to 2\pi$时,摆线会走过刚好一个周期

• 分别作$A\perp x$交于$P$,$A\perp C^{\prime }Q$交于$D$

  • $AD$=$PQ$=$a\sin t$
  • $x$=$OQ-PQ$=$\stackrel{⌢}{\mathrm{AQ}}$-$PQ$=$ta-a\sin t$=$a(t-\sin t)$
  • $y$=$AP$=$DQ$=$C^{\prime }Q-C^{\prime }D$=$a-a\cos t$=$a(1-\cos t)$

参数方程

• 综上:摆线的方程为$x=a(t-\sin t)$(1);$y=a(1-\cos t)$(2)

普通方程

• 这里利用公式$\sin (\arccos t)$=$\sqrt{1-{\cos }^2(\arccos t)}$=$\sqrt{1-t^2}$(3)
  • 这里$\arccos t\in [0,\pi ]$,$\sin (\arccos t)⩾0$
• 而由(2)可以解出$t$=$\arccos (1-\frac{y}{a})$,(4);代入(1),得$x$=$a(\arccos (1-\frac{y}{a})-\sin (\arccos (1-\frac{y}{a})))$=$a\arccos (1-\frac{y}{a})-a\sqrt{1-(1-\frac{y}{a}{)}^2}$=$a\arccos (1-\frac{y}{a})-\sqrt{y(2a-y)}$(5)
• 因此普通方程可以写成:$x$=$a\arccos (1-\frac{y}{a})-\sqrt{y(2a-y)}$(6),形式复杂,不如参数方程来得简单

星形线

• 与摆线类似但不同,摆线沿着直线摆动,而星形线验证圆线内切的摆动

• 参数方程

  • $x=r{\cos }^{3}t$
  • $y=r{\sin }^{3}t$

• 普通方程

  • $x^{\frac{2}{3}}+y^{\frac{2}{3}}$=$r^{\frac{2}{3}}$