本文主要是介绍FIR和IIR去噪算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- FIR—有限冲激响应滤波器概述
- FIR滤波器中的卷积
- 对比
- octave滤波器设计
- FIR滤波器设计
- audioread函数用法
- 高频噪声和低频噪声的区别
- 信号的频域分析——频谱、能量谱、功率谱、倒频谱、小波分析
- 汉明窗
- fir1函数
- FIR窗函数设计
- 低通滤波器的设计
- 三角窗(巴特利特Barlett窗)
- 傅里叶变换
- 波形图
- IIR滤波器
- YUV颜色模型
- 高斯噪声和椒盐噪声
- 高斯白噪声
- 中值滤波
FIR—有限冲激响应滤波器概述
FIR(Finite Impulse Response)有限脉冲响应滤波器,有限说明其脉冲响应是有限的。只用当前和过去的输入样点值来得到当前的输出样点值,该滤波器以前的输出样点一个也未用到(FIR被称为非递归滤波器的原因)。
给定一个有限持续时间的非0输入值,结果是FIR总有一个有限持续时间的非0输出值,如果FIR的输入突然变成一个全为0,则该滤波器的输出最后也全为0。
FIR滤波器使用加法计算其输出,平均器的作用就像一个低通滤波器,平滑了输入中的突然变化。单位延迟,指示一个移位寄存器,在输出计算期间,输入值被暂时存放在其中。
5抽头FIR滤波器
了解如何预测当各种频率的正弦样点作为输入时该滤波器的行为表现,即如何估计它们的频域响应。频域响应的两个影响因素:抽头数和用于乘系数的特定值。
FIR滤波器中的卷积
冲激响应:当输入是一个单一的单位样值(冲激)且前后的样值都是0时滤波器的时域输出序列。
滤波器的系数(或冲激响应)使用值不全相同的系数,能改进我们的滤波器的性能(让所需要的信号通过让不需要的信号衰减的能力)。
对比
与IIR相比,它具有线性相位、容易设计的优点。FIR比IIR需要更多的参数。这也就说明,要增加DSP的计算量。DSP需要更多的计算时间,对DSP的实时性有影响。
FIR 滤 波器 具 有非 递 归 、 稳 定 性 好 、精 度 高 、积 累 误 差 小 、易 于 计 算 机 辅 助设 计 等 优 点[7-8],但 存 在 计 算 量 大 的 缺 点 。在满 足 幅 度 响 应 要 求 的 同 时 ,可 以 获 得 严 格 的 线 性 相位 。 然 而 ,由 于 阶 次 较 高 ,FIR 滤 波 器 的 延 迟 也 要 比 同 样性 能 的 IIR 滤 波 器 大 得 多 。
IIR 滤 波 器 具有 结 构 简 单 、效 率 高 、与 模 拟 滤 波 器 有 对 应 关 系 、易 于 解析 控 制 及 计 算 机 辅 助 设 计 等 优 点 [9], 但 稳 定 性 较 差 , 易产 生 溢 出 、噪 声 、误 差 。 利 用 数 字 滤 波 器 ,可 改 变 信 号 中所 含 频 率 分 量 的 相 对 比 例 或 滤 除 某 些 频 率 分 量 。
octave滤波器设计
FIR滤波器设计
$ help fir1得到以下内容:
-- Function File: B = fir1 (N, W)-- Function File: B = fir1 (N, W, TYPE)-- Function File: B = fir1 (N, W, TYPE, WINDOW)-- Function File: B = fir1 (N, W, TYPE, WINDOW, NOSCALE)
根据给定的截止频率W,生成一个N阶FIR滤波器,返回B中的N+1滤波系数。
如果W是一个标量,指定低通或高通滤波器的截止频率;如果W是一个双元素向量,这两个值指定带通或带阻滤波器的边;如果W是一个n元向量,值指定多频带通过/停止过滤器的频带边缘。
滤波器类型可以用以下字符串之一指定:低、高、停止、通过、带通、DC-0或DC-1。W是一个标量默认为”低”,W是一对默认为“通过”,W是一个大于2个元素的向量默认为“DC-0”。
可选的形状窗口可以给出一个带有长度N+1的向量,没有指定,则使用长度为N+1的汉明窗(Hamming)。
在“noscale”选项中,过滤器系数不存在归一化。归一化过滤器的默认值是第一通带中心的幅值响应为1。
audioread函数用法
[y,Fs] = audioread(filename)
[y,Fs] = audioread(filename,samples)
[y,Fs] = audioread(___,dataType)
- 输入
filename指要读取的文件名称,注意引号和文件后缀
samples指读取文件的区域,举个例子,如果文件有100个数据那么长,如果读取前一半的数据,此处应为[1,50]
datatype指读取后文件的数据格式,如double和native
- 输出
y是读出数据
Fs为音频文件的采样率
高频噪声和低频噪声的区别
正常人耳能听见的频率范围是20Hz到20000Hz
-
频率范围:低频:主频率低于300Hz;高频:主频率高于800Hz
-
危害:低频比高频危害大
-
相同距离衰减速度:低频衰减慢,高频衰减快‘
低频噪音与高频噪音不同,高频噪音是那种很尖利的声音,波长很短,随着距离越远或遭遇dao障碍物,能迅速衰减,如高频噪音的点声源泉每10米距离就能下降6分贝。而低频噪音声音分贝不高,却递减得很慢,波长很长,因此能够长距离直入人耳,比如变压器的电流声,大型冷柜机的声音都属于低频噪音。
信号的频域分析——频谱、能量谱、功率谱、倒频谱、小波分析
- 频谱:将信号做傅里叶变换从而进行分析。包括幅频谱(常用)和相频谱两张图。
汉明窗
语音信号一般在10ms到30ms之间,我们可以把它看成是平稳的。为了处理语音信号,我们要对语音信号进行加窗,也就是一次仅处理窗中的数据。因为实际的语音信号是很长的,我们不能也不必对非常长的数据进行一次性处理。明智的解决办法就是每次取一段数据,进行分析,然后再取下一段数据,再进行分析。
怎么仅取一段数据呢?一种方式就是构造一个函数。这个函数在某一区间有非零值,而在其余区间皆为0.汉明窗就是这样的一种函数。它主要部分的形状像sin(x)在0到pi区间的形状,而其余部分都是0.这样的函数乘上其他任何一个函数f,f只有一部分有非零值。
为什么汉明窗这样取呢?因为之后我们会对汉明窗中的数据进行FFT,它假设一个窗内的信号是代表一个周期的信号。(也就是说窗的左端和右端应该大致能连在一起)而通常一小段音频数据没有明显的周期性,加上汉明窗后,数据形状就有点周期的感觉了。
因为加上汉明窗,只有中间的数据体现出来了,两边的数据信息丢失了,所以等会移窗的时候,只会移1/3或1/2窗,这样被前一帧或二帧丢失的数据又重新得到了体现。
fir1函数
b = fir1(n,Wn)
%设计具有线性相位的n阶低通、带通或多频FIR滤波器。
b = fir1(n,Wn,ftype)
%设计低通,高通,带通,带阻或多频带滤波器,取决于ftype的值和Wn的元素数量。
b = fir1(___,window)
%使用window中指定的向量和先前语法中的任何参数设计过滤器。
b = fir1(___,scaleopt)
%另外指定滤波器的幅度响应是否被归一化。
- n——滤波器阶数
- Wn——截止频率,0~1,Wn=1对应于采样频率的一半
- 当设计带通和带阻滤波器时,Wn=[W1 W2]
- ftype——设计高通和带阻滤波器,ftype=high时,设计高通FIR滤波器,=stop时设计带阻FIR滤波器。低通和带通FIR滤波器无需输入ftype参数。
- Windows——窗函数。窗函数的长度应等于FIR滤波器系数个数,即阶数n+1。
- b——生成的滤波器系数
对于具有任意频率响应的窗口滤波器,使用fir2。
B = fir2 (N, F, M)
B = fir2 (N, F, M, GRID_N)
B = fir2 (N, F, M, GRID_N, RAMP_N)
B = fir2 (N, F, M, GRID_N, RAMP_N, WINDOW)
函数fir2用来设计多通带任意响应FIR滤波器
该滤波器的幅频特性由向量对f和m确定,f为归一化频率向量,m为对应频率点上的幅度。当设计的滤波器在频率为π的幅度响应不是0时,滤波器的阶数n为偶数
参数f为频率点矢量,矢量f按升序排列,且第一个元素必须是0,最后一个必须为1,并可以包含重复的频率点
矢量m中包含了与f相对应的期望得到的滤波器的幅度。
低通:低频通过
高通:高频通过
带通:一定频率范围通过
带阻:阻止一定频率范围的信号
FIR窗函数设计
- 确定滤波器类型,I型可设计LP(低通)、HP(高通)、BP(带通)、BS(带阻)滤波器;
| Fir I型 | Fir II型 | Fir III型 | Fir IV型 |
|---|---|---|---|
| LP,HP,BP,BS | LP,BP | BP | HP,BP,BS |
- 确定设计的滤波器的参数
低通滤波器的设计
设计一个低通滤波器先要明白要截止多大的频率。比如想截掉4Hz以上的信号,理想状态下就是将4Hz以上的信号成分全部截止,4Hz以下的信号全部保留。然而事实上几乎不存在这样的滤波器,通常情况下总是在通过频率和截止频率之间存在一个过渡带,通过频率这部分称为通带,允许通过的最大频率为通带截止频率ωp,截止频率这部分称为阻带,阻带最小截止频率为ωs,通带和阻带之间的部分为过渡带,即ωp~ωp。通带之间的波动称为通带波动δp,阻带之间的波动称为阻带波动δs。
数字滤波器设计中,Wp和Ws为归一化角频率,如果工程要求设计低通数字滤波器满足通带截止频率为fp = 40,阻带截止频率fs = 50,则fp,fs和Wp,Ws之间的转换关系为:
Wp = 2* pi* fp/Fs;
Ws = 2* pi*fs/Fs;
截止频率的定义是当输出幅值响应下降到输入幅值的-3dB( [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gP48lsiH-1611552445567)(https://www.zhihu.com/equation?tex=20log%281%2F%5Csqrt%7B2%7D%29)] ),也就是0.707(也就是 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9kqEupeA-1611552445569)(https://www.zhihu.com/equation?tex=1%2F%5Csqrt%7B2%7D)] )时对应的频率,也称3db截频
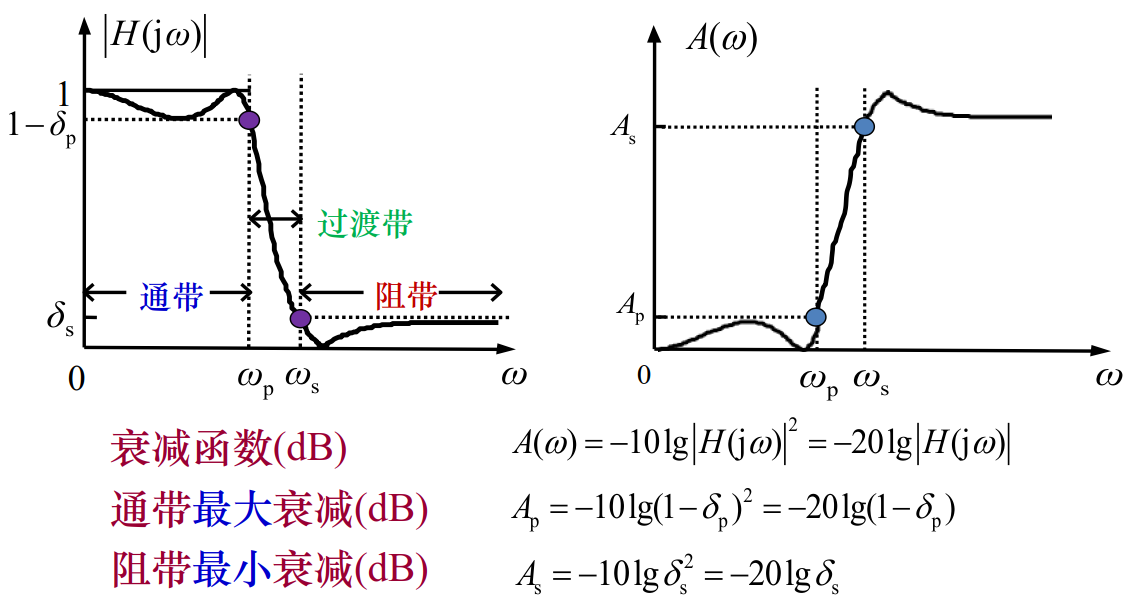
Ap:通带最大衰减;As:阻带最小衰减
滤波器有部分频率是通,部分是阻。但是阻的部分,未必能全部阻隔,而只有部分衰减,部分留下来,因此最小衰减就可以描述它阻碍该阻碍的波段的能力的高低。最小衰减越大,能力越好。
对于特定区间的w,衰减-80dB也就是增益为-80dB,即20lg|A(w)|=-80。可知A(w)=10(-4),也就是说,在输入频率为w(rad/s)的正弦波信号作用下,输出幅值将为输入信号幅值的10(-4)倍,即0.00001倍。
因此,所谓阻带衰减-80dB,就是在一个特定的w区间段上,输出信号相对输入信号幅值缩小一万倍。
三角窗(巴特利特Barlett窗)
矩形窗从0到1(或1到0)有一个突变的过渡带,造成了吉布斯现象。
barlett提出了一种逐渐过渡的三角窗形式,它是两个矩形窗的卷积。
w=bartlett(n):
- 输入参数n是窗函数的长度;
- 输出参数w是由窗函数的值组成的n阶向量;
- 巴特利特窗是两个矩形窗的卷积;
- 此函数生成的巴特利特窗的两端总是0;
- 与三角形函数非常类似,当n是奇数时,则有Bartlett(n+2)的中间部分等于triang(n);当n是偶数时,巴特利特窗的傅立叶变换是负数。
傅里叶变换
傅立叶变换任何一个输入信号都可以使用多个余弦波叠加而成,即把时序信号转换成频域信息。我们需要找到这些余弦波的相关参数:幅值、相位。
波形图
- 波越高,说明振幅越大,响度就越大;
- 波越密,说明振动的越快;
- 频率越高,音调就越高。
IIR滤波器
在连续系统中采用拉普拉斯变换求解微分方程,并直接定义了传递函数,成为研究系统的基本工具。在采样系统中,连续变量变成了离散量,将Laplace变换用于离散量中,就得到了Z变换。和拉氏变换一样,Z变换可用来求解差分方程
数字滤波器的功能本质上是将一组输入数字序列通过一定的运算转变为另一组输出数字序列。
IIR滤波器常见的结构形式有直接I型、直接II型、级联型、并联型。
在IIR滤波器设计过程中,通常利用模拟滤波器来设计数字滤波器,要先根据滤波器的性能指标设计出相应的模拟滤波器的系统函数H(s)
YUV颜色模型
“Y”表示明亮度,也就是灰阶值;而“U”和“V”表示的是色度,作用是描述影像色彩及饱和度,用于指定像素的颜色。
YUV颜色模型解决了彩色图像和黑白图像的兼容问题,如果只有Y信号而没有U和V信号,那么一幅彩色图像就可以背转换为黑白图像。
高斯噪声和椒盐噪声
高斯噪声是指噪声符合高斯分布,即某个强度的噪声点个数最多,离这个强度越远噪声点个数越少,且这个规律服从高斯分布,高斯噪声是一种加性噪声,即噪声直接加到原图像上,可以用线性滤波器滤除。
椒盐噪声类似把椒盐撒在图像上,是一种在图像上出现很多白点或黑点的噪声,如电视里的雪花噪声等,可以认为是一种逻辑噪声,用线性滤波器滤除的结果不好。一般采用中值滤波器滤波可以得到较好的效果。
经高斯滤波后看不到原始图像的特征。分析原因:高斯白噪声的频带覆盖了整个频谱,会将原始图像的频谱淹没。如果此时仍然使用带通滤波器很难再将原有的图像恢复。在网络上查阅资料不难发现,高斯白噪声较好的滤除方法是中值滤波。
高斯白噪声
白噪声,如同白光一样,是所有颜色的黄叠加而成,不同颜色的光本质区别是它们的频率各不相同。白噪声在功率谱上趋近为常值,即噪声频率丰富,在整个频谱上都有成分,即从低频到高频,低频指的是信号不变或缓慢变化,高频指的是信号突变。
由傅立叶变换性质可知,时域有限,频域无限;频域有限,时域无限。那么频域无限的信号变换到时域上,对应于冲击函数的整数倍,即说明在时间轴的某点上,噪声孤立,与其他的噪声无关,
中值滤波
将图像3×3的矩阵的9个像素点排序,这个矩阵的中心点赋值为这九个像素的中值。
这篇关于FIR和IIR去噪算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








