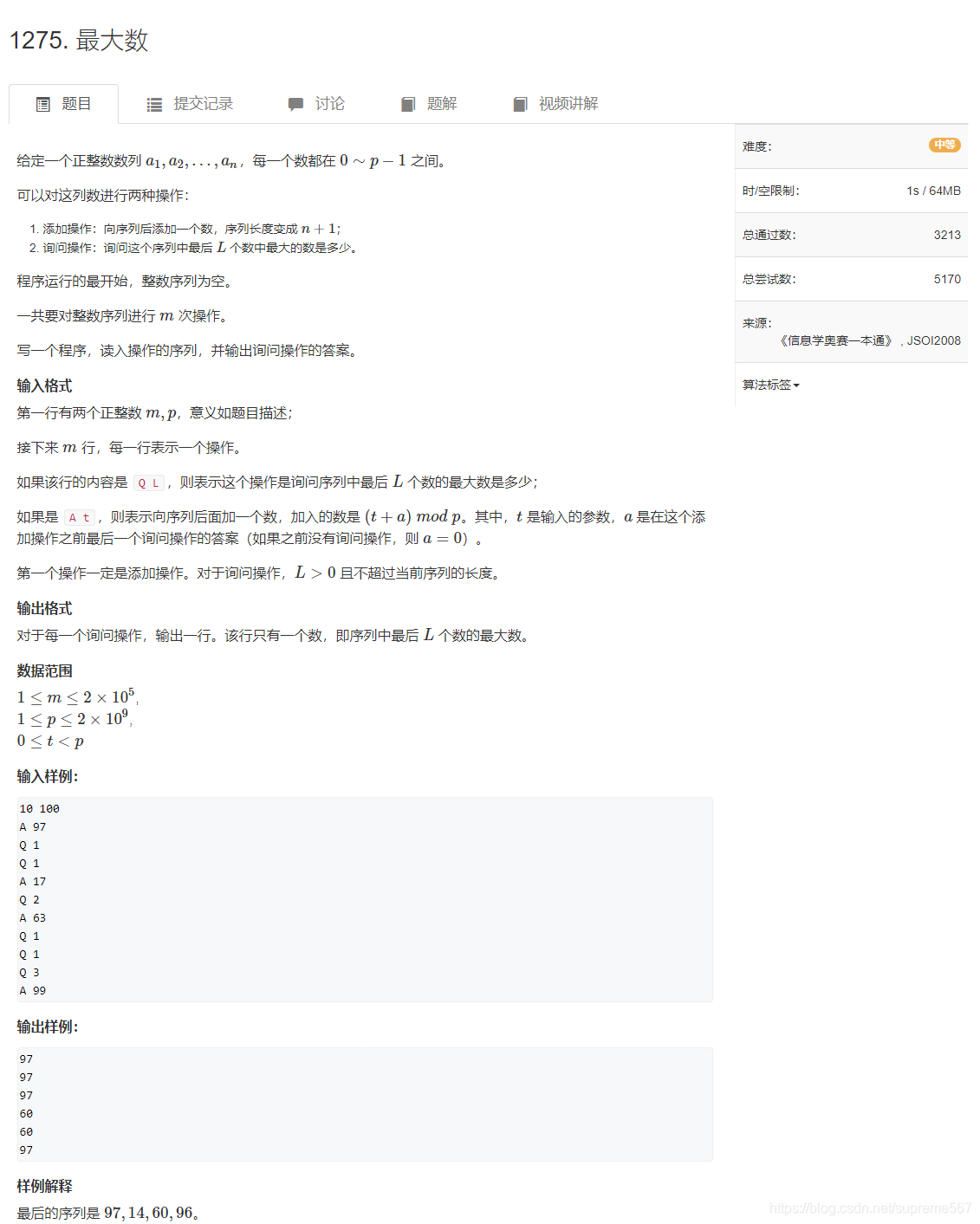
本文主要是介绍线段树(扫描线法,单点修改区间查询,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 200010;int m, p;
struct Node
{int l, r;int v; // 区间[l, r]中的最大值
}tr[N * 4];void pushup(int u) // 由子节点的信息,来计算父节点的信息
{tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v);
}void build(int u, int l, int r)
{tr[u] = {l, r};if (l == r) return;int mid = l + r >> 1;build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}int query(int u, int l, int r)
{if (tr[u].l >= l && tr[u].r <= r) return tr[u].v; // 树中节点,已经被完全包含在[l, r]中了int mid = tr[u].l + tr[u].r >> 1;int v = 0;if (l <= mid) v = query(u << 1, l, r);if (r > mid) v = max(v, query(u << 1 | 1, l, r));return v;
}void modify(int u, int x, int v)
{if (tr[u].l == x && tr[u].r == x) tr[u].v = v;else{int mid = tr[u].l + tr[u].r >> 1;if (x <= mid) modify(u << 1, x, v);else modify(u << 1 | 1, x, v);pushup(u);}
}int main()
{int n = 0, last = 0;scanf("%d%d", &m, &p);build(1, 1, m);int x;char op[2];while (m -- ){scanf("%s%d", op, &x);if (*op == 'Q'){last = query(1, n - x + 1, n);printf("%d\n", last);}else{modify(1, n + 1, (last + x) % p);n ++ ;}}return 0;
}

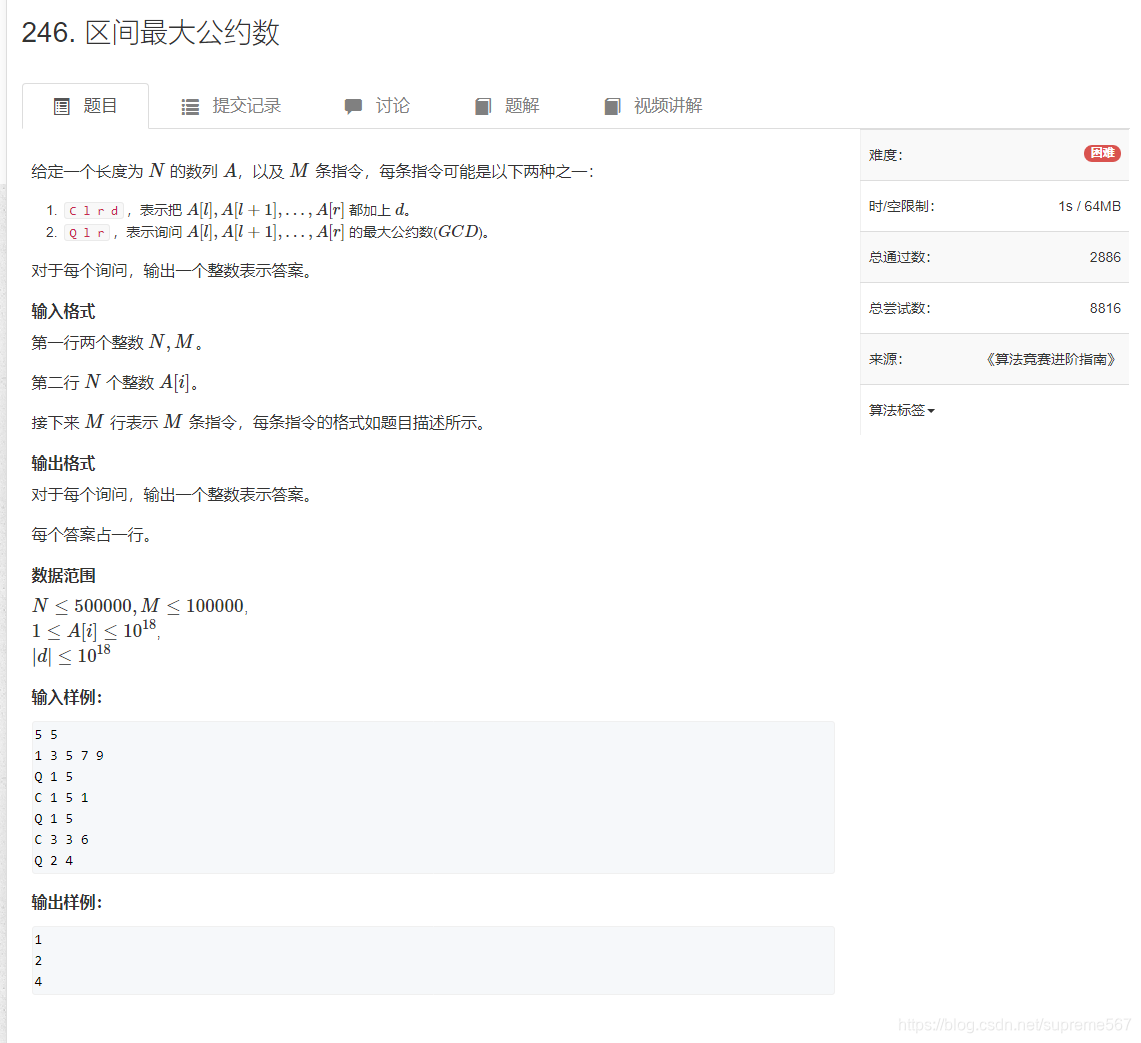
线段树,懒标记(这道题需要两个懒标记,而且要根据加和·乘运算变成一个运算
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 100010;
int n,w[N],p;
struct node{int l,r,sum,add,mul;
}tr[4*N];
void pushup(int u){tr[u].sum=(tr[u<<1].sum+tr[u<<1|1].sum)%p;
}
// void eval(node &t,int add,int mul){
// t.sum=(t.sum*mul+add)%p;
// t.add=(t.add*mul+add)%p;
// t.mul=(t.mul*mul)%p;
// }
void eval(int u,int add,int mul){tr[u].sum=(tr[u].sum*mul %p+ (tr[u].r-tr[u].l+1)*add )%p;tr[u].add=(tr[u].add*mul+add)%p;tr[u].mul=(tr[u].mul*mul)%p;}
void pushdown(int u){eval(u<<1,tr[u].add,tr[u].mul);eval(u<<1|1,tr[u].add,tr[u].mul);tr[u].mul=1;tr[u].add=0;
}
void build(int u,int l,int r){if(l==r)tr[u]={l,r,w[r],0,1};else{tr[u]={l,r,0,0,1};int mid=l+r>>1;build(u<<1,l,mid);build(u<<1|1,mid+1,r);pushup(u);}
}void modify(int u,int l,int r,int add,int mul){if(tr[u].l>=l&&tr[u].r<=r)eval(u,add,mul);else{pushdown(u);int mid=tr[u].l+tr[u].r>>1;if(mid<r)modify(u<<1|1,l,r,add,mul);if(mid>=l)modify(u<<1,l,r,add,mul);pushup(u);}
}
int query(int u,int l,int r){if(tr[u].l>=l&&tr[u].r<=r)return tr[u].sum;pushdown(u);int mid=tr[u].l+tr[u].r>>1;int ans=0;if(mid>=l)ans=query(u<<1,l,r);if(mid<r)ans=(ans+query(u<<1|1,l,r) )%p;return ans;
}
signed main(){cin>>n>>p;for(int i=1;i<=n;i++)cin>>w[i];build(1,1,n);int t;cin>>t;while(t--){int op,l,r;cin>>op>>l>>r;if(op==2){int add;cin>>add;modify(1,l,r,add,1);}else if(op==1){int mul;cin>>mul;modify(1,l,r,0,mul);}else cout<<query(1,l,r)<<endl;}
}
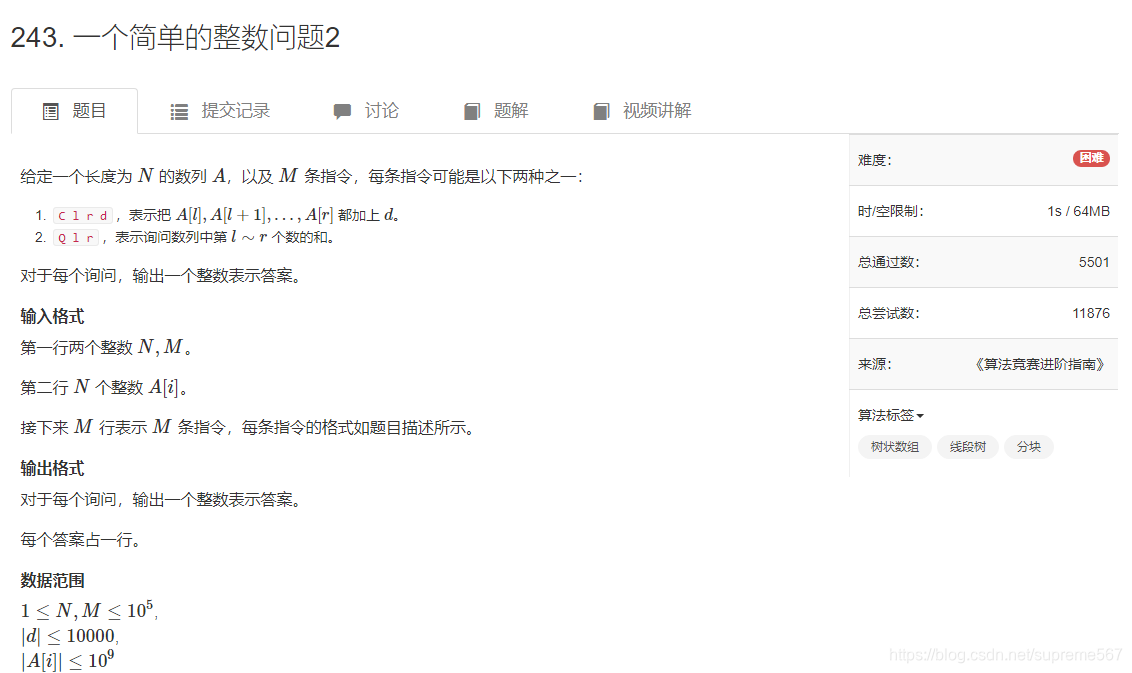
利用差分的思想和更相减损法求gcd知识,不用懒标记实现单点修改区间查询
#include<bits/stdc++.h>
#define node Node
using namespace std;
typedef long long LL;
#define int long long
const int N = 500010;
int n,m,w[N];
struct node{int l,r,sum,d;
}tr[N*4];int gcd(int a,int b){return b?gcd(b,a%b):a;
}void pushup(node & t,node & a,node &b){t.sum=a.sum+b.sum;t.d=gcd(a.d,b.d);
}
void pushup(int u){pushup(tr[u],tr[u<<1],tr[u<<1|1]);
}void build(int u, int l, int r)
{if (l == r){LL b = w[r] - w[r - 1];tr[u] = {l, r, b, b};}else{tr[u].l = l, tr[u].r = r;int mid = l + r >> 1;build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);pushup(u);}
}void modify(int u,int x,int v){if(tr[u].l==x&&tr[u].r==x){// tr[u].sum+=v;// tr[u].d+=v;int b=tr[u].sum+v;tr[u]={x,x,b,b};}else{int mid= tr[u].l+tr[u].r>>1;if(mid<x)modify(u<<1|1,x,v);else modify(u<<1,x,v);pushup(u);}
}Node query(int u, int l, int r)
{if (tr[u].l >= l && tr[u].r <= r) return tr[u];else{int mid = tr[u].l + tr[u].r >> 1;if (r <= mid) return query(u << 1, l, r);else if (l > mid) return query(u << 1 | 1, l, r);else{auto left = query(u << 1, l, r);auto right = query(u << 1 | 1, l, r);Node res;pushup(res, left, right);return res;}}
}signed main(){cin>>n>>m;for(int i=1;i<=n;i++)cin>>w[i];build(1,1,n);while(m--){char c;int l,r;cin>>c>>l>>r;if(c=='C'){int v;cin>>v;modify(1,l,v);//差分思想,l~r这段区间加上一个数要在l加上去,在r+1减回去if(r+1<=n)modify(1,r+1,-v);//边界}else{node left=query(1,1,l);node right={0,0,0,0};if(l+1<=r)right=query(1,l+1,r);cout<<abs( gcd(left.sum , right.d ) )<<endl;}}
}


我真的吐了我靠这个线段树的边界条件居然这么苛刻

只有这样才是正确的·
我快吐了woc


#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 100010;
int n,w[N],m;struct node{int l,r,sum,add;
}tr[N*4];void pushup(int u){tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
}
void pushdown(int u){auto &left=tr[u<<1];auto &right=tr[u<<1|1];auto &root=tr[u];if(root.add){left.add+=root.add,left.sum+=(left.r-left.l+1)*root.add;right.add+=root.add,right.sum+=(right.r-right.l+1)*root.add;root.add=0;}
}
void build(int u,int l,int r){if(l==r)tr[u]={l,r,w[l],0};else{tr[u]={l,r};int mid=l+r>>1;build(u<<1,l,mid);build(u<<1|1,mid+1,r);pushup(u);}
}void modify(int u,int l,int r,int v){if(tr[u].l>=l&&tr[u].r<=r){tr[u].sum+= (tr[u].r-tr[u].l+1)*v;tr[u].add+=v;}else{pushdown(u);int mid=tr[u].l+tr[u].r>>1;if(l<=mid)modify(u<<1,l,r,v);if(mid<r)modify(u<<1|1,l,r,v);pushup(u);}
}int query(int u,int l,int r){if(tr[u].l>=l&&tr[u].r<=r)return tr[u].sum;else{pushdown(u);int mid=tr[u].l+tr[u].r>>1;int ans=0;if(l<=mid)ans=query(u<<1,l,r);if(mid<r)ans+=query(u<<1|1,l,r);pushup(u);return ans;}
}signed main(){cin>>n>>m;for(int i=1;i<=n;i++)cin>>w[i];build(1,1,n);char op[2];int l,r;while(m--){scanf("%s%d%d",op,&l,&r);//cout<<*op<<endl;if(*op=='Q')cout<<query(1,l,r)<<endl;else{int v;cin>>v;modify(1,l,r,v);}}
}

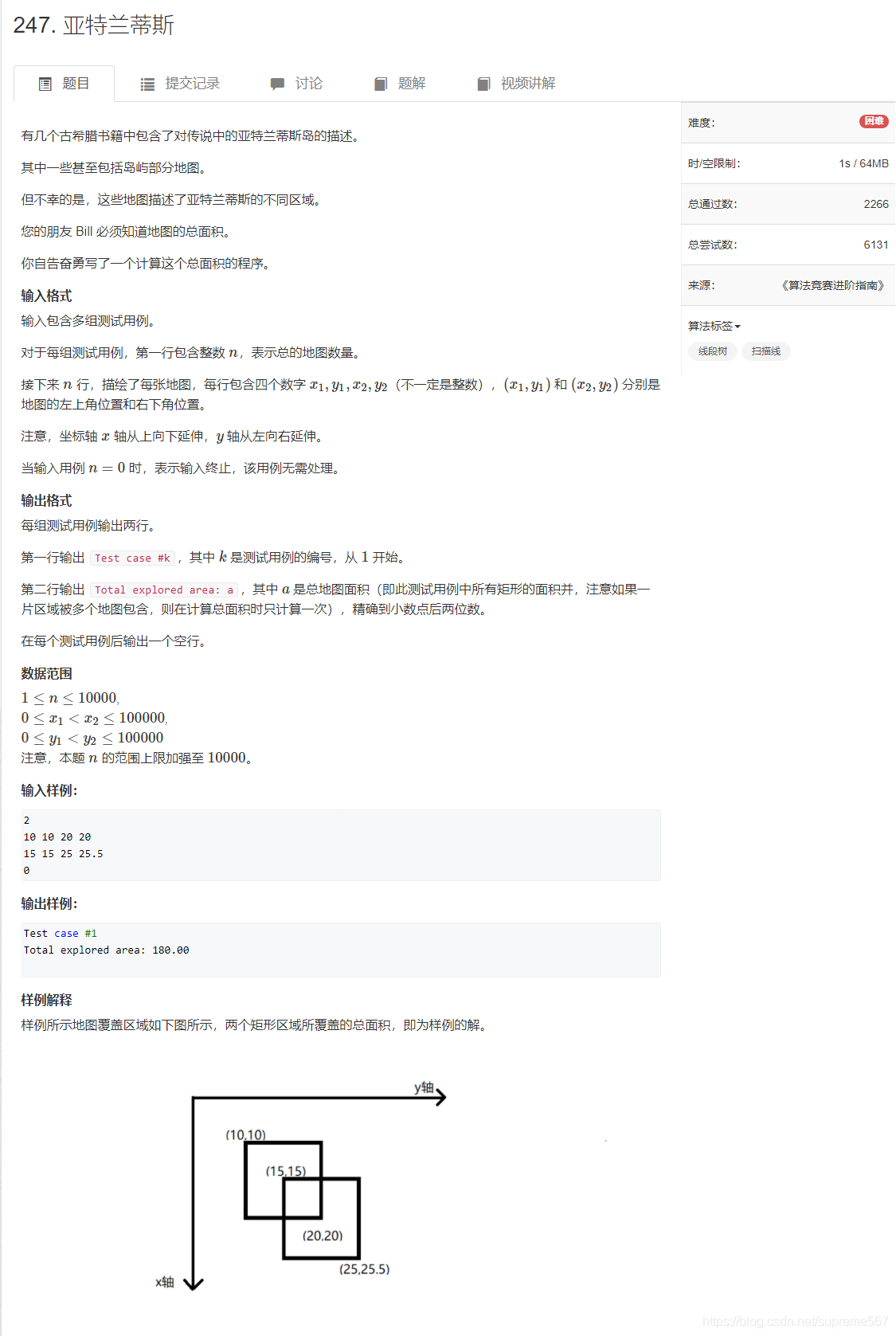
这道题·维护的东西有点多
lmax表示最大前缀和
rmax表示最大后缀和
tmax表示最大子串和
sum表示求和
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 500010;int n, m;
int w[N];
struct Node
{int l, r;int sum, lmax, rmax, tmax;
}tr[N * 4];void pushup(Node &u, Node &l, Node &r)
{u.sum = l.sum + r.sum;u.lmax = max(l.lmax, l.sum + r.lmax);u.rmax = max(r.rmax, r.sum + l.rmax);u.tmax = max(max(l.tmax, r.tmax), l.rmax + r.lmax);
}void pushup(int u)
{pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}void build(int u, int l, int r)
{if (l == r) tr[u] = {l, r, w[r], w[r], w[r], w[r]};else{tr[u] = {l, r};int mid = l + r >> 1;build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);pushup(u);}
}void modify(int u, int x, int v)
{if (tr[u].l == x && tr[u].r == x) tr[u] = {x, x, v, v, v, v};else{int mid = tr[u].l + tr[u].r >> 1;if (x <= mid) modify(u << 1, x, v);else modify(u << 1 | 1, x, v);pushup(u);}
}Node query(int u, int l, int r)
{if (tr[u].l >= l && tr[u].r <= r) return tr[u];else{int mid = tr[u].l + tr[u].r >> 1;if (r <= mid) return query(u << 1, l, r);else if (l > mid) return query(u << 1 | 1, l, r);else{auto left = query(u << 1, l, r);auto right = query(u << 1 | 1, l, r);Node res;pushup(res, left, right);return res;}}
}int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);build(1, 1, n);int k, x, y;while (m -- ){scanf("%d%d%d", &k, &x, &y);if (k == 1){if (x > y) swap(x, y);printf("%d\n", query(1, x, y).tmax);}else modify(1, x, y);}return 0;
}
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>using namespace std;const int N = 100010;int n;
struct Segment
{double x, y1, y2;int k;bool operator< (const Segment &t)const{return x < t.x;}
}seg[N * 2];
struct Node
{int l, r;int cnt;double len;
}tr[N * 8];vector<double> ys;int find(double y)
{return lower_bound(ys.begin(), ys.end(), y) - ys.begin();
}void pushup(int u)
{if (tr[u].cnt) tr[u].len = ys[tr[u].r + 1] - ys[tr[u].l];else if (tr[u].l != tr[u].r){tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;}else tr[u].len = 0;
}void build(int u, int l, int r)
{tr[u] = {l, r, 0, 0};if (l != r){int mid = l + r >> 1;build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);}
}void modify(int u, int l, int r, int k)
{if (tr[u].l >= l && tr[u].r <= r){tr[u].cnt += k;pushup(u);}else{int mid = tr[u].l + tr[u].r >> 1;if (l <= mid) modify(u << 1, l, r, k);if (r > mid) modify(u << 1 | 1, l, r, k);pushup(u);}
}int main()
{int T = 1;while (scanf("%d", &n), n){ys.clear();for (int i = 0, j = 0; i < n; i ++ ){double x1, y1, x2, y2;scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);seg[j ++ ] = {x1, y1, y2, 1};seg[j ++ ] = {x2, y1, y2, -1};ys.push_back(y1), ys.push_back(y2);}sort(ys.begin(), ys.end());ys.erase(unique(ys.begin(), ys.end()), ys.end());build(1, 0, ys.size() - 2);sort(seg, seg + n * 2);double res = 0;for (int i = 0; i < n * 2; i ++ ){if (i > 0) res += tr[1].len * (seg[i].x - seg[i - 1].x);modify(1, find(seg[i].y1), find(seg[i].y2) - 1, seg[i].k);}printf("Test case #%d\n", T ++ );printf("Total explored area: %.2lf\n\n", res);}return 0;
}作者:yxc
链接:https://www.acwing.com/activity/content/code/content/167934/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
线段树学了一天了,加油加油
这篇关于线段树(扫描线法,单点修改区间查询的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







