本文主要是介绍遗传算法(Genetic Algorithm,GA)求解不闭合多旅行商问题(提供MATLAB代码),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、遗传算法(GA)介绍
遗传算法(Genetic Algorithm,GA)是一种模拟自然界生物进化过程的优化算法。它通过模拟生物的遗传、变异和选择等机制,来搜索问题的最优解。
遗传算法的基本思想是通过对候选解进行编码,然后通过模拟自然界的进化过程,逐代地进行选择、交叉和变异操作,以产生新的候选解,并逐步优化这些候选解,直到找到满足特定条件的最优解。
具体来说,遗传算法包括以下几个关键步骤:
1. 初始化种群:随机生成一组初始候选解,称为种群。
2. 评估适应度:根据问题的特定评价函数,对种群中的每个候选解进行评估,得到适应度值。
3. 选择操作:根据适应度值,选择一部分优秀的候选解作为父代。
4. 交叉操作:从父代中选择两个个体,通过某种方式进行基因交换,生成新的子代。
5. 变异操作:对子代中的某些基因进行随机变异,引入新的基因组合。
6. 更新种群:将子代加入到种群中,替换掉部分父代。
7. 重复执行步骤2至步骤6,直到满足终止条件(如达到最大迭代次数或找到满意的解)。
遗传算法的优点是可以在大规模搜索空间中找到较好的解,适用于各种优化问题,如函数优化、组合优化、路径规划等。
二、遗传算法求解不闭合多旅行商问题
2.1部分代码
close all
clear
clc
AlgorithName='GA';
%数据集参考文献 REINELT G.TSPLIB-a traveling salesman problem[J].ORSA Journal on Computing,1991,3(4):267-384.
global data StartPoint Tnum
% 导入TSP数据集 bayg29
load('data.txt')
Tnum=4;%旅行商个数(可以自行更改)2-6
StartPoint=1; %选择起点城市(可以自行更改)
Dim=size(data,1)-1;%维度
lb=-10;%下界
ub=10;%上界
fobj=@Fun;%计算总距离
SearchAgents_no=100; % 种群大小(可以修改)
Max_iteration=500; % 最大迭代次数(可以修改)
Algorith=str2func(AlgorithName);
[fMin,bestX,curve]=Algorith(SearchAgents_no,Max_iteration,lb,ub,Dim,fobj);
2.2部分结果
(1)6个旅行商
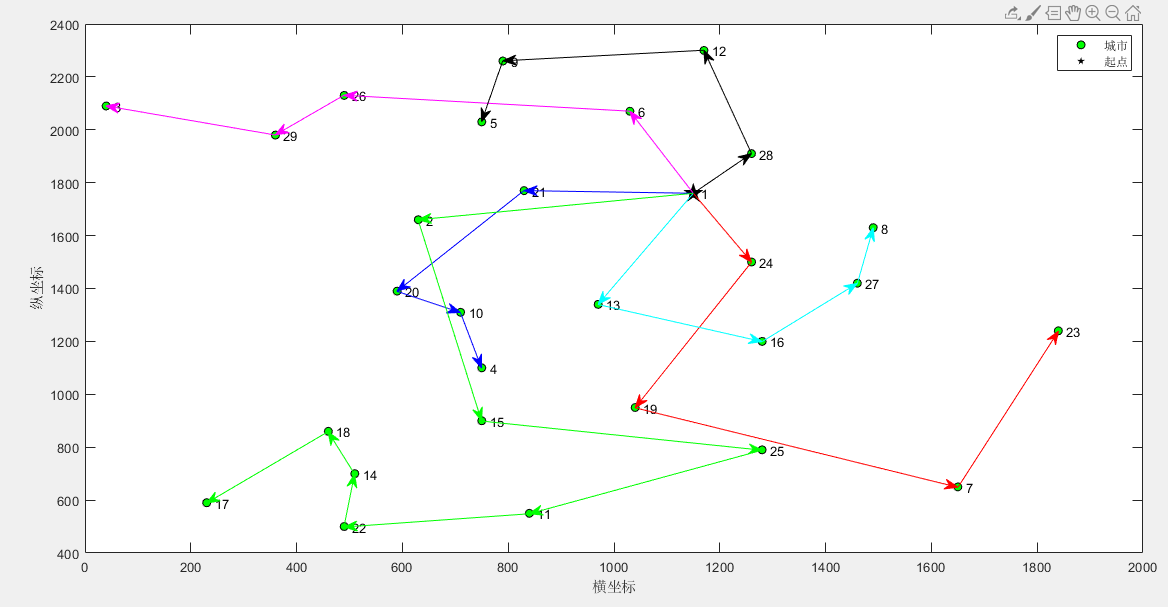
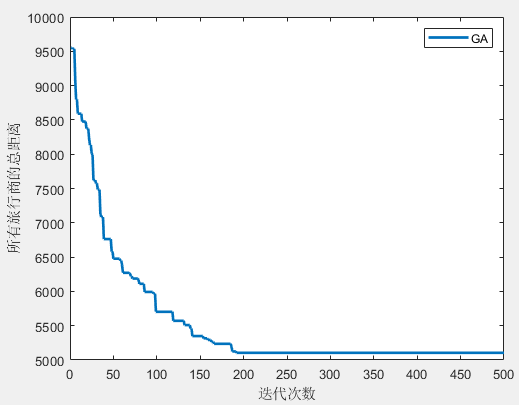
第1个旅行商的路径:1->24->19->7->23
第1个旅行商的总路径长度:1130.000000
第2个旅行商的路径:1->6->26->29->3
第2个旅行商的总路径长度:748.064168
第3个旅行商的路径:1->21->20->10->4
第3个旅行商的总路径长度:609.097693
第4个旅行商的路径:1->13->16->27->8
第4个旅行商的总路径长度:671.043963
第5个旅行商的路径:1->28->12->9->5
第5个旅行商的总路径长度:628.728876
第6个旅行商的路径:1->2->15->25->11->22->14->18->17
第6个旅行商的总路径长度:1317.535578
所有旅行商的总路径长度:5104.470279
(2)5个旅行商
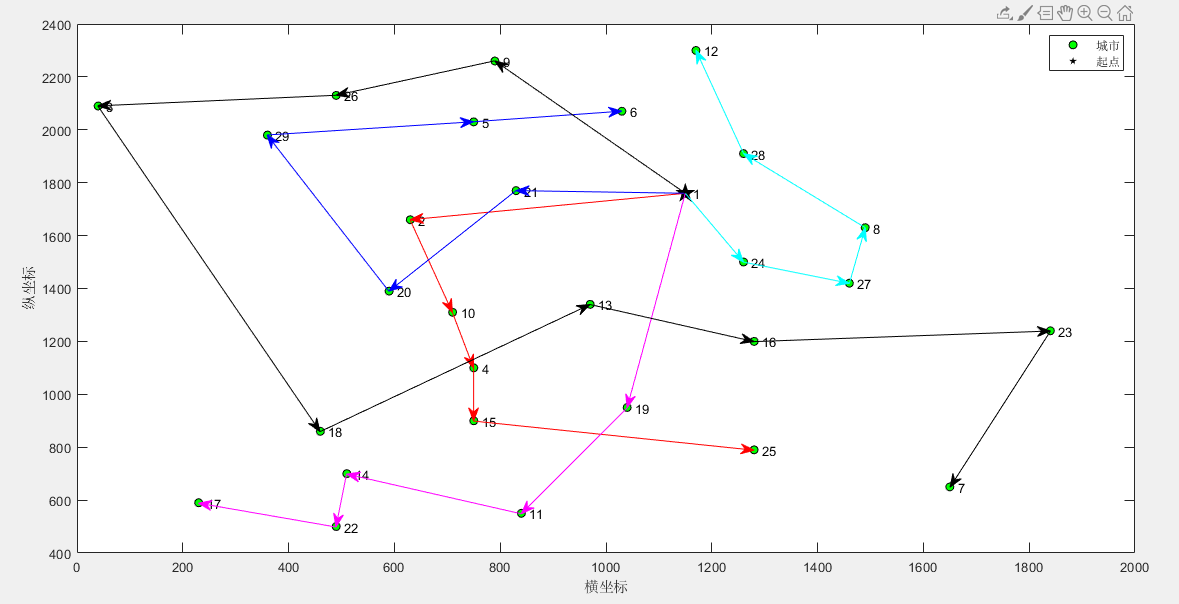
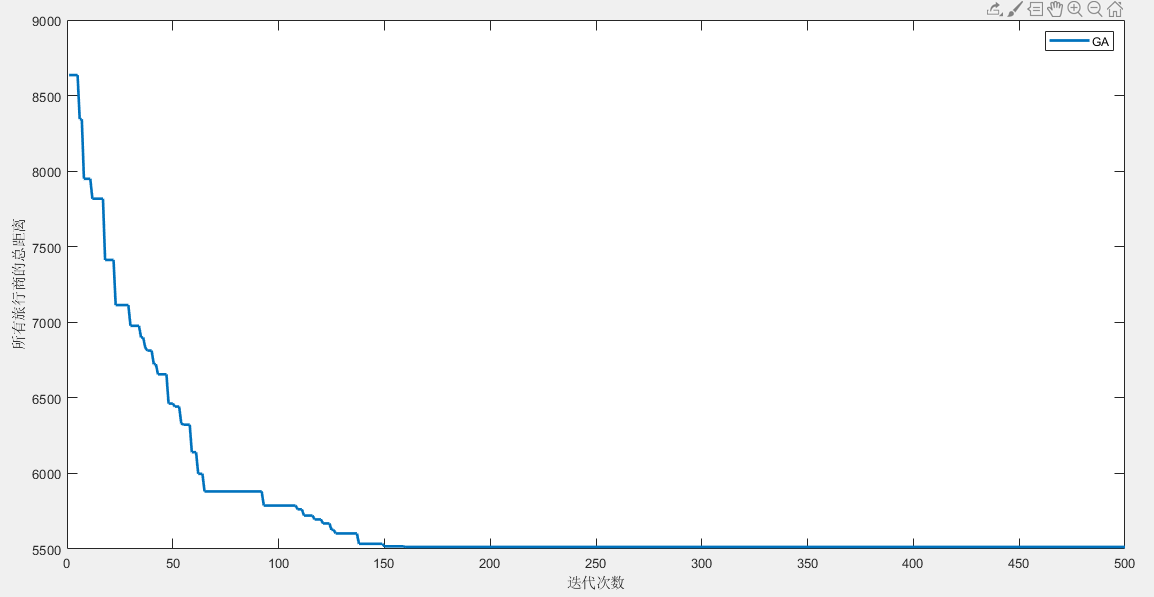
第1个旅行商的路径:1->2->10->4->15->25
第1个旅行商的总路径长度:887.693641
第2个旅行商的路径:1->19->11->14->22->17
第2个旅行商的总路径长度:1056.267012
第3个旅行商的路径:1->21->20->29->5->6
第3个旅行商的总路径长度:969.587541
第4个旅行商的路径:1->24->27->8->28->12
第4个旅行商的总路径长度:680.147043
第5个旅行商的路径:1->9->26->3->18->13->16->23->7
第5个旅行商的总路径长度:1919.765611
所有旅行商的总路径长度:5513.460847
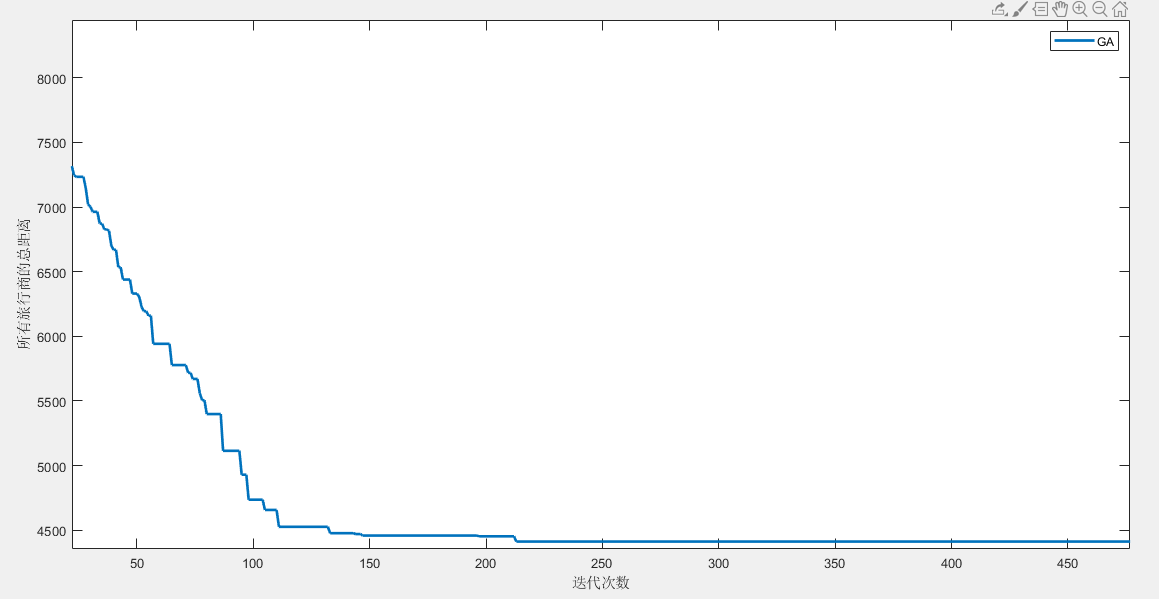
(3)4个旅行商
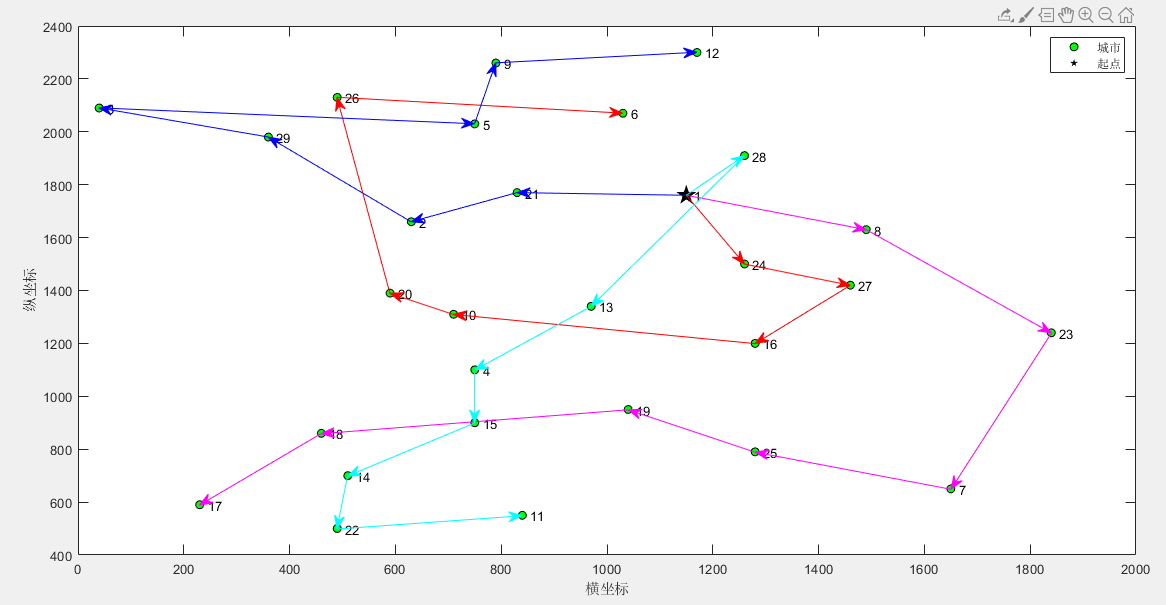
第1个旅行商的路径:1->24->27->16->10->20->26->6
第1个旅行商的总路径长度:1190.588090
第2个旅行商的路径:1->8->23->7->25->19->18->17
第2个旅行商的总路径长度:1225.275479
第3个旅行商的路径:1->21->2->29->3->5->9->12
第3个旅行商的总路径长度:1073.592101
第4个旅行商的路径:1->28->13->4->15->14->22->11
第4个旅行商的总路径长度:923.363417
所有旅行商的总路径长度:4412.819088
三、完整MATLAB代码
这篇关于遗传算法(Genetic Algorithm,GA)求解不闭合多旅行商问题(提供MATLAB代码)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





