本文主要是介绍计组原理 : 计算机可靠性概述和性能评价,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、 计算机可靠性概述
计算机系统的可靠性指它开始运行( t = 0 ) 到某时刻 t 这段时间内能正常运行的概率。 用 R(t) 表示。失效率即单位时间内失效的元件数与总数的比例。用λ表示
![]()
两次故障之间系统能正常工作的时间的平均值称为平均无故障时间(MTTF) 。是衡量一个产品(尤其是电器产品)的可靠性指标。可靠性可以定义为当用户访问服务时,服务按预期运行的可能性。通常用MTTF,来反映无失效运作的概率 即
MTTF = 1 / λ
可靠性 = MTTF/(1+MTTF)
MTBF “平均故障间隔时间”用来表示计算机的可用性。此度量描述服务运行的时间百分比,这也被称为服务的“正常运行时间”,
可用性 = MTBF/(1+MTBF)
通常用平均修复时间(MTTR)来表示计算机的可维修性(完成维护的概率)。指从故障发生到机器修复平均所需要的时间。因此在计算机任意时刻能正常工作的概率A,可表示为
A = MTTF / (MTTF + MTTR)
可维护性 = 1 /(1+MTTR)
可以看出:
MTBF = MTTF + MTTR
而 MTTR 远小于MTTF ,因此 MTTF 近似于MTBF。
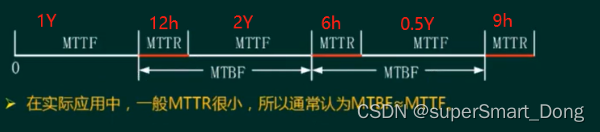
例如:在上图中,截止目前某个系统的运行情况如上图,从t0时刻上线起,共故障了3回。
那么 平均无故障时间MTTF = (1+2+0.5)/3 *365 *24 小时=10220 小时,
平均故障修复时间MTTR = (12+6+9)/3小时=9小时
平均故障间隔时间 MTBF = MTTF +MTTR = 10220 +9小时 =10229小时
如果一个系统有N个子系统,各个子系统的可靠性分别用 Rn 表示 。
对于 串联系统,该系统的可靠性R,可表示为
R = R1 × R2 × R3 ...× RN
失效率 λ 可表示为
λ = λ1 + λ2 + λ3 .... +λn
对于并联系统该系统的可靠性R,可表示为
R = 1- (1-R1)(1-R2)(1-R3).....(1-Rn)
失效率 λ 可表示为

对于 N模冗余系统 ,N=2n+1个子系统,和一个表决器组成,表决器把N个子系统中占大多数的输出多为系统的输出,因此只要有n+1 个子系统能正常工作。假设表决器完全可靠的,每个子系统可靠性为R0,则N模冗余系统的可靠性为
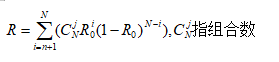
注:
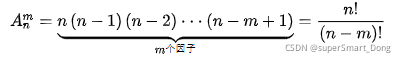
例1:一个系统由3个子系统并联构成,其可靠性为0.9,平均无故障时间为10000小时。求系统的可靠性和平均无故障时间
R1 =R2 =R3 =0.9;
并联系统的计算机可靠性:R = 1- (1-Ri)^3 = 1 - 0.1 ^3 =0.999
子系统失效率 λ1 = λ2= λ3=1/10000
系统失效率 λ = 1/(1/(1/10000) *(1/1 +1/2 +1/3))
系统平均无故障时间 MTBF = 1/λ = 1/(1/10000) *(1/1 +1/2 +1/3) ≈18333小时
例2:对于一个混合系统其可靠性如下:
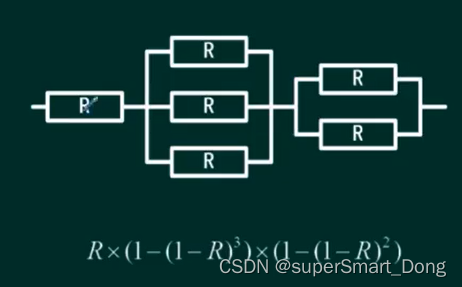
二、计算机的性能评测的常用方法
1)时钟频率。一般来讲主频越高,速度越快。但是对于频率相同,不同结构的机器,其速度可能差很多。
2)指令执行速度。即单位时间内执行指令的条数。对于不同的指令执行速率不同,但是在早期,通常用加法指令的运算速度来衡量计算机的速度,因为加法大体可以反映出乘法等其他运算速度。
3)等效指令速度法。统计各类指令在程序中所占比例,和各类指令的执行时间,那么等效指令的执行时间为
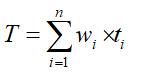
4)数据处理速率(PDR)法。在不同程序中的各类指令使用步履是不同的,而且数据长度与指令功能的强弱对解题速度影响极大。同时以上的方法不能反应出现代计算机中高速缓冲存储器、流水线和交叉存储等架构影响。因此,现代计算机不仅与指令的执行频率有关,而且与指令的执行顺序和地址分布有关。 PDR 值越大, 性能越好。
PDR = L / R
其中 L=0.85G + 0.15H+ 0.4J +0.15K ; R =0.85M +0.09N +0.06 P
G:每条定点指令位数 ; M:平均定点加法时间
H::每条浮点指令位数 N:平均浮点加法时间
J:定点操作数位数 N:平均浮点乘法时间
K:定点操作数位数
5)核心程序法:把应用程序中用的最频繁的核心不同在不同的机器上运行,测其执行时间。作为各类机器性能评价依据
这篇关于计组原理 : 计算机可靠性概述和性能评价的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






