VIO第4讲：基于滑动窗口法的vio系统可观性与一致性

本文主要是介绍VIO第4讲：基于滑动窗口法的vio系统可观性与一致性，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

VIO第4讲基于滑动窗口算法的 VIO 系统：可观性和一致性

1 从高斯分布到信息矩阵

1.1 SLAM和高斯分布

  考虑某个状态$\mathbf{\xi }$（如位姿T、路标点P），以及一次与该变量相关的观测$r_i$。由于噪声的存在，观测服从概率分布$p\left({\mathbf{r}}_i|\mathbf{\xi }\right)$

  多次观测时，各个测量值相互独立，则多个测量$\mathbf{r}={\left({\mathbf{r}}_1,\dots ,{\mathbf{r}}_n\right)}^{\top }$构建的似然概率为：
$$L(\xi )=L(r_1,r_2,\cdots ,r_n;\xi )=p(\mathbf{r}|\mathbf{\xi })=\prod _{i}p\left({\mathbf{r}}_i|\mathbf{\xi }\right)$$
  此时，观测r就是样本，而状态如位姿T就是待估计参数。$L(\xi )$就是样本的似然函数，也是事件{$R_1=r_1,R_2=r_2,\cdots ,R_n=r_n$}发生的概率.

  如果知道机器人状态的先验信息$p(\mathbf{\xi })$，即GPS，轮速计等提供了状态的初始值。利用贝叶斯法则，有后验概率分布：
$$p(\mathbf{\xi }|\mathbf{r})=\frac{p(\mathbf{r}|\mathbf{\xi })p(\mathbf{\xi })}{p(\mathbf{r})}$$
  但实际情况中很难具体求出这个后验概率分布，所以只能估计最大后验概率，就像下面图中绿色的点。
$${\mathbf{\xi }}_{\mathrm{MAP}}=\arg \underset{\mathbf{\xi }}{\max }p(\mathbf{\xi }|\mathbf{r})$$

$${\mathbf{\xi }}_{\mathrm{MAP}}=\arg \underset{\xi }{\max }\prod _{i}p\left({\mathbf{r}}_i|\mathbf{\xi }\right)p(\mathbf{\xi })$$
  进一步，在没有先验的情况下，最大后验估计MAP就是最大似然估计MLP，通俗讲，就是说在什么样的状态下，最可能产生现在观测状态到的数据。

  对上面式子取对数，再取负，那么求原函数最大也就是求下式最小！
$${\mathbf{\xi }}_{\mathrm{MAP}}=\arg \underset{\mathbf{\xi }}{\min }\left[-\sum _i\log p\left({\mathbf{r}}_i|\mathbf{\xi }\right)-\log p(\mathbf{\xi })\right]$$
  假设观测值r服从多元高斯分布，对应最大似然估计–参数估计—以位姿为例，估计位姿均值和协方差。（因为高斯分布的均值出概率最大！）
$$p\left({\mathbf{r}}_i|\mathbf{\xi }\right)=\mathcal{N}\left({\mathbf{\mu }}_i,{\mathbf{\Sigma }}_i\right),p\left(\mathbf{\xi }\right)=\mathcal{N}\left({\mathbf{\mu }}_{\xi },{\mathbf{\Sigma }}_{\xi }\right)$$
  对应到最小二乘里面，有如下形式
$${\mathbf{\xi }}_{\mathrm{MAP}}=\underset{\mathbf{\xi }}{\mathrm{argmin}}\sum _i\Vert {\mathbf{r}}_i-{\mathbf{\mu }}_i{\Vert }_{{\mathbf{\Sigma }}_i}^2+{\Vert \mathbf{\xi }-{\mathbf{\mu }}_{\xi }\Vert }_{{\mathbf{\Sigma }}_{\xi }}^2$$

1.2 协方差矩阵与信息矩阵

  十四讲中讲过协方差矩阵与信息矩阵的关系：由于观测之间应该是不相关的，那么相应的协方差矩阵就会“小”，对于的信息矩阵就会“大”，所以这个误差项会在问题中占有较高的权重。

参考论文：The humble Gaussian distribution里面的例子很形象

2 舒尔补应用：边际概率、条件概率

2.1 舒尔补

维基百科

给定任意的矩阵块 M，如下所示:

$$\mathbf{M}=\left[\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ \mathbf{C}& \mathbf{D}\end{array}\right]$$

1 如果，矩阵块 D 是可逆的，则$\mathbf{A}-\mathbf{B}{\mathbf{D}}^{-1}\mathbf{C}$称之为D关于M的舒尔补

2 如果，矩阵块 A 是可逆的，则$\mathbf{D}-{\mathbf{CA}}^{-1}\mathbf{B}$称之为A关于M的舒尔补

  舒尔补是用于把一个矩阵进行高斯消元，变为上三角或下三角矩阵

$$\begin{gathered} [\begin{array}{cc}\mathbf{I}& 0\\ -{\mathbf{CA}}^{-1}& \mathbf{I}\end{array}]\left[\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ \mathbf{C}& \mathbf{D}\end{array}\right]=\left[\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ 0& {\Delta }_{\mathbf{A}}\end{array}\right] \\ \left[\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ \mathbf{C}& \mathbf{D}\end{array}\right]\left[\begin{array}{cc}\mathbf{I}& -{\mathbf{A}}^{-1}\mathbf{B}\\ 0& \mathbf{I}\end{array}\right]=\left[\begin{array}{cc}\mathbf{A}& 0\\ \mathbf{C}& {\Delta }_{\mathbf{A}}\end{array}\right] \end{gathered}$$
  其中，${\Delta }_{\mathbf{A}}=\mathbf{D}-\mathbf{C}{\mathbf{A}}^{-1}\mathbf{B}$。联合起来就可以把矩阵变为对角矩阵：
$$[\begin{array}{cc}\mathbf{I}& 0\\ -\mathbf{C}{\mathbf{A}}^{-1}& \mathbf{I}\end{array}]\left[\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ \mathbf{C}& \mathbf{D}\end{array}\right]\left[\begin{array}{cc}\mathbf{I}& -{\mathbf{A}}^{-1}\mathbf{B}\\ 0& \mathbf{I}\end{array}\right]=\left[\begin{array}{cc}\mathbf{A}& 0\\ 0& {\Delta }_{\mathbf{A}}\end{array}\right]$$
  反之，也可以从对角矩阵恢复为矩阵M
$$[\begin{array}{cc}\mathbf{I}& 0\\ {\mathbf{CA}}^{-1}& \mathbf{I}\end{array}]\left[\begin{array}{cc}\mathbf{A}& 0\\ 0& {\Delta }_{\mathbf{A}}\end{array}\right]\left[\begin{array}{cc}\mathbf{I}& {\mathbf{A}}^{-1}\mathbf{B}\\ 0& \mathbf{I}\end{array}\right]=\left[\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ \mathbf{C}& \mathbf{D}\end{array}\right]$$
  利用这个舒尔补，也可以快速的求解矩阵M的逆：
$${[\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ \mathbf{C}& \mathbf{D}\end{array}]}^{-1}=\left[\begin{array}{cc}\mathbf{I}& -{\mathbf{A}}^{-1}\mathbf{B}\\ 0& \mathbf{I}\end{array}\right]\left[\begin{array}{cc}{\mathbf{A}}^{-1}& 0\\ 0& {\Delta }_{\mathbf{A}}^{-1}\end{array}\right]\left[\begin{array}{cc}\mathbf{I}& 0\\ -\mathbf{C}{\mathbf{A}}^{-1}& \mathbf{I}\end{array}\right]$$

2.2 舒尔补的应用

  假设多元变量 x 服从高斯分布，且由两部分组成$\mathbf{x}=[\begin{array}{c}a\\ b\end{array}]$，变量之间构成的协方差矩阵为：
$$\mathbf{K}=[\begin{array}{cc}A& C^{\top }\\ C& D\end{array}]$$
  其中，$A=\mathrm{cov}(a,a),D=\mathrm{cov}(b,b),C=\mathrm{cov}(a,b)$，由此变量x的概率分布为：
$${P(a,b)=P(a)P(b|a)\propto \exp (-\frac{1}{2}[\begin{array}{c}a\\ b\end{array}]}^{\top }{\left[\begin{array}{cc}A& C^{\top }\\ C& D\end{array}\right]}^{-1}\left[\begin{array}{c}a\\ b\end{array}\right])$$
  舒尔补对协方差的逆进行分解，得到边际概率$\mathsf{p}(\mathsf{a})$和条件概率$\mathrm{p}(b|a)$.
$$\begin{array}{rl}& P(a,b)\\ & {\propto \exp (-\frac{1}{2}[\begin{array}{c}a\\ b\end{array}]}^{\top }{\left[\begin{array}{cc}A& C^{\top }\\ C& D\end{array}\right]}^{-1}\left[\begin{array}{c}a\\ b\end{array}\right])\\ & {\propto \exp (-\frac{1}{2}[\begin{array}{c}a\\ b\end{array}]}^{\top }\left[\begin{array}{cc}I& -A^{-1}{C}^{\top }\\ 0& I\end{array}\right]\left[\begin{array}{cc}{A}^{-1}& 0\\ 0& {\Delta }_{\mathrm{A}}^{-1}\end{array}\right]\left[\begin{array}{cc}I& 0\\ -C{A}^{-1}& I\end{array}\right]\left[\begin{array}{c}a\\ b\end{array}\right])\\ & \propto \exp (-\frac{1}{2}[\begin{array}{cc}{a}^{\top }& (b-C{A}^{-1}a{)}^{\top }\end{array}]\left[\begin{array}{cc}{A}^{-1}& 0\\ 0& {\Delta }_{\mathbf{A}}^{-1}\end{array}\right]\left[\begin{array}{c}a\\ b-C{A}^{-1}a\end{array}\right])\\ & \propto \exp \left(-\frac{1}{2}\left(a^{\top }{A}^{-1}a\right)+{\left(b-C{A}^{-1}a\right)}^{\top }{\Delta }_{\mathbf{A}}^{-1}\left(b-C{A}^{-1}a\right)\right)\\ & \propto \underset{p(a)}{\underbrace{\exp \left(-\frac{1}{2}{a}^{\top }{A}^{-1}a\right)}}\underset{p(b|a)}{\underbrace{\exp \left(-\frac{1}{2}{\left(b-C{A}^{-1}a\right)}^{\top }{\Delta }_{\mathbf{A}}^{-1}\left(b-C{A}^{-1}a\right)\right)}}\end{array}$$

2.2.1 结论1

2.2.2 结论2

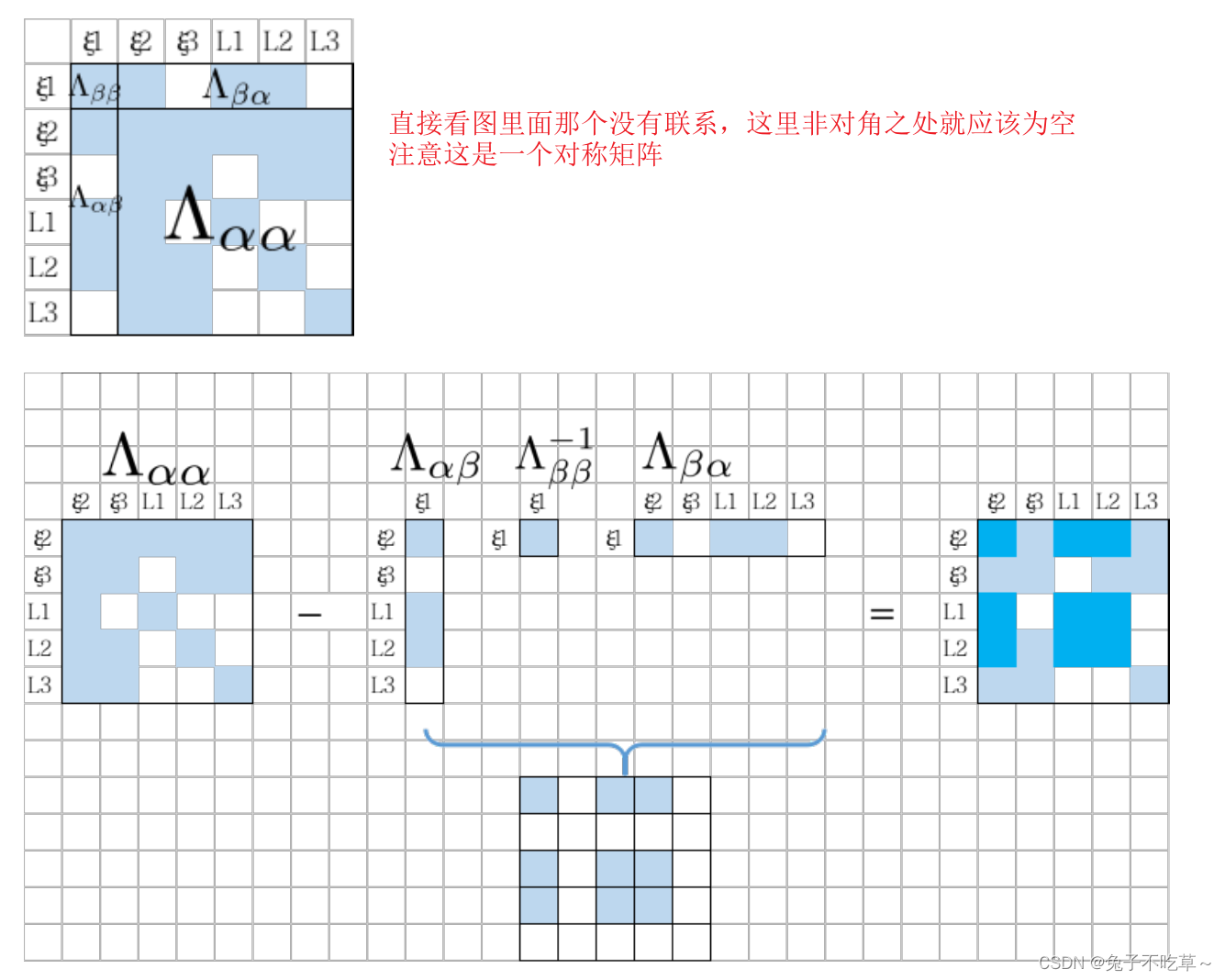
  就是说边际概率的协方差本来应该是A，它的信息矩阵就是$A^{-1}$。然后就是说，在两个变量的协方差矩阵的逆，信息矩阵的组成元素中，可以通过下面38式得到边际概率的信息矩阵。

  下面这个例子也能看出来，比如说，我们求变量x1x2的一个信息矩阵，利用x1x2x3的信息矩阵就可以直接求出来，相当于消除了变量x3！把左上角看作一个块，就可以代入上面的公式！代入公式刚好就是相应x1x2的信息矩阵！

2.2.3 总结

3 滑动窗口算法与边缘化 Marginalization

3.1 最小二乘的图表示

3.2 最小二乘问题信息矩阵的构成

  上面最小二乘的高斯牛顿解：
$$\underset{\text{H }or\mathbf{\Lambda }}{\underbrace{{\mathbf{J}}^{\top }{\mathbf{\Sigma }}^{-1}\mathbf{J}}}\delta \mathbf{\xi }=\underset{\mathbf{b}}{\underbrace{-{\mathbf{J}}^{\top }{\mathbf{\Sigma }}^{-1}\mathbf{r}}}$$
  其中，雅可比矩阵为：
$$\mathbf{J}=\frac{\partial \mathbf{r}}{\partial \mathbf{\xi }}=\left[\begin{array}{c}\frac{\partial {\mathbf{r}}_{12}}{\partial \mathbf{\xi }}\\ \frac{\partial {\mathbf{r}}_{13}}{\partial \mathbf{\xi }}\\ \frac{\partial {\mathbf{r}}_{14}}{\partial \mathbf{\xi }}\\ \frac{\partial {\mathbf{r}}_{15}}{\partial \mathbf{\xi }}\\ \frac{\partial {\mathbf{r}}_{56}}{\partial \mathbf{\xi }}\end{array}\right]=\left[\begin{array}{c}{\mathbf{J}}_1\\ {\mathbf{J}}_2\\ {\mathbf{J}}_3\\ {\mathbf{J}}_4\\ {\mathbf{J}}_5\end{array}\right],{\mathbf{J}}^{\top }=\left[\begin{array}{ccccc}{\mathbf{J}}_1^{\top }& {\mathbf{J}}_2^{\top }& {\mathbf{J}}_3^{\top }& {\mathbf{J}}_4^{\top }& {\mathbf{J}}_5^{\top }\end{array}\right]$$

  除了写为一个大的矩阵，还可以把矩阵写为连加求和的形式：
$$(\sum _{i=1}^5{\mathbf{J}}_i^{\top }{\mathbf{\Sigma }}_i^{-1}{\mathbf{J}}_i)\delta \mathbf{\xi }=-\sum _{i=1}^5{\mathbf{J}}^{\top }{\mathbf{\Sigma }}_i^{-1}\mathbf{r}$$
  矩阵乘法的分配率$(A+B)x=Ax+Bx=b_1+b_2=b$,所以求和形式相当于矩阵的加法，其并不会改变实际的结果。（因为优化变量x就是固定那几个，所以求和展开是等效的）。
  假设我有n个误差边，m个优化变量，n>>m，不论n是多大，雅可比矩阵也仍然是m*m，由n个叠加而成。(注意m是指多个优化变量雅可比的维度叠加，m=位姿6p+路标点3l)

3.3 信息矩阵的稀疏性

  很明显，不可能所有的状态之间都存在着关联，所以雅可比矩阵大概率是一个稀疏矩阵

3.4 信息矩阵组装过程的可视化

  上面我们已经得知，可以将残差的信息矩阵加起来得到最终的信息矩阵，其结果不变

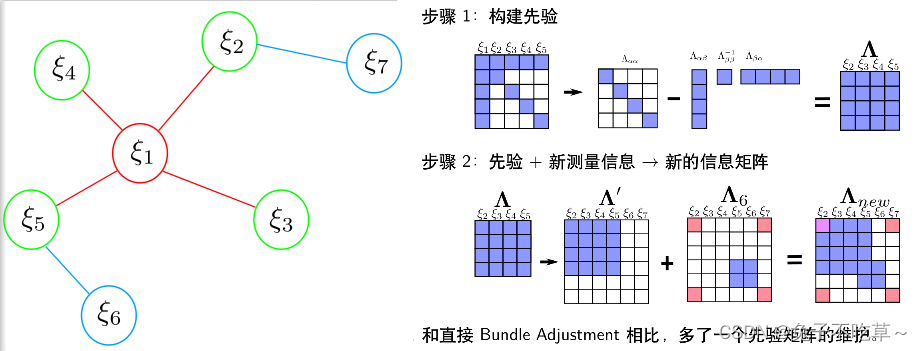
3.5 基于边际概率(Marginalization)的滑动窗口算法

这里可以看崔华坤推导vins里面的例子，滑动窗口的特点就是不能随意的抛弃某一帧，要通过舒尔补的方式将其转换为先验信息，加入到剔除这一帧的信息矩阵中！

  随着 VSLAM 系统不断往新环境探索，就会有新的相机姿态以及看到新的环境特征，最小二乘残差就会越来越多，信息矩阵越来越大，计算量将不断增加。
  为了保持优化变量的个数在一定范围内，需要使用滑动窗口算法动态增加或移除优化变量。

滑动窗口算法大致流程

1 增加新的变量进入最小二乘系统优化

2 如果变量数目达到了一定的维度，则利用边际概率移除老的变量

3 SLAM 系统不断循环前面两步

  论文Exactly sparse extended information filters for feature-based SLAM，如果直接丢弃，会损失那部分状态所带来的先验信息，不能保留状态直接按的约束关系。

marginalization边缘化使得信息矩阵变得稠密！

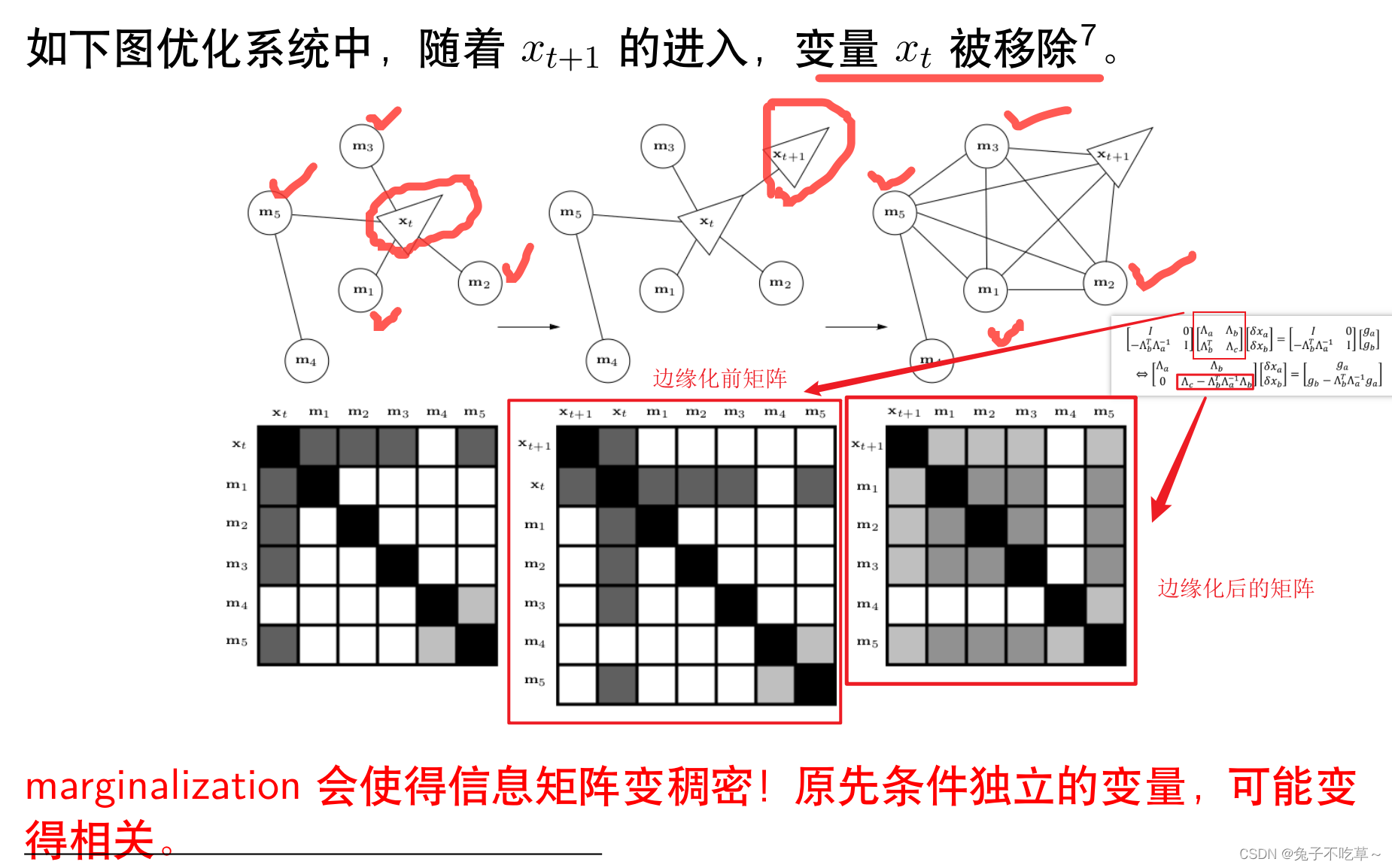
崔华坤VINS推导里面有一个很形象的例子，可以参考。下面这个图和上面例子基本一致

3.6 VINS中的滑动窗口算法

​ VINS 根据次新帧是否为关键帧，分为两种边缘化策略：通过对比次新帧和次次新帧的视差量，来决定 marg 掉次新帧或者最老帧

① 当次新帧为关键帧时，MARGIN_OLD，将 marg 掉最老帧，及其看到的路标点和相关联的 IMU 数据，将其转化为先验信息加到整体的目标函数中

② 当次新帧不是关键帧时，MARGIN_SECOND_NEW，我们将直接扔掉次新帧及它的视觉观测边，而不对次新帧进行 marg，因为我们认为当前帧和次新帧很相似，也就是说当前帧跟路标点之间的约束和次新帧与路标点的约束很接近，直接丢弃并不会造成整个约束关系丢失过多信息。但是值得注意的是，我们要保留次新帧的 IMU 数据，从而保证 IMU 预积分的连贯性。

直接扔掉不会保留相应的观测信息，边缘化则是将其转换为先验信息

4 滑动窗口中的FEJ算法

4.1 滑动窗口算法导致的问题

	边缘化marg会导致优化变量2自身的信息矩阵由两部分组成

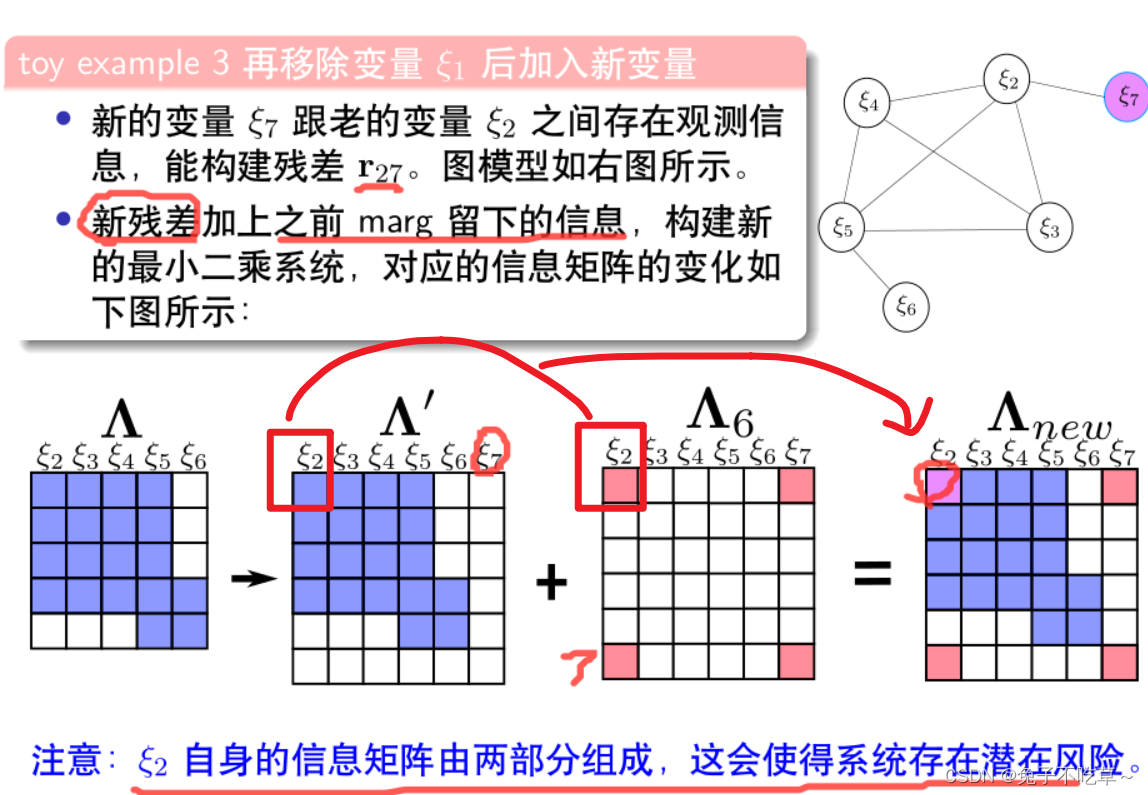
  滑动窗口算法中，对于同一个变量，不同残差对其计算雅克比矩阵时线性化点可能不一致，导致信息矩阵可以分成两部分，相当于在信息矩阵中多加了一些信息，使得其零空间出现了变化。进而多个解的问题，变成了一个确定解，不可观的变量，变成了可观。比如后续的纯视觉实验中，本来有7个自由度不可观，但因为增加了一些其它信息，只有5个自由度不可观。

4.2 可观性

4.2.1 什么是可观？

① 线性系统理论中的可观测性

  线性系统可观性是判断系统是否能由系统的观测得到的一种性质。

  一个线性系统是可观测的，当且仅当通过观测器可以从系统的输出推断出系统的全部状态信息。这意味着，如果系统的某些状态不能从输出中推断出来，那么该系统就是不可观测的。

  线性系统的可观测性可以通过判断系统的观测矩阵的秩来进行。具体而言，如果系统的观测矩阵（通常称为可观测矩阵）的秩等于系统状态的个数，则该系统是可观测的。反之，如果观测矩阵的秩小于状态的个数，则该系统是不可观测的。

  也可以通过下面的奇异值SVD分解来做这个事情，如果分解之后存在为0的奇异值，那么说明这个系统存在不可观的维度！因为矩阵H不满秩。

② SLAM系统中的可观测性

如果一个系统完全能观，其一定满秩，不会存在零空间。对于单目VO系统，我们要优化的是位姿、路标点等状态量，但是实际的测量值像素位置是不会发生变化的，也就是说，输出不能推断出系统的状态的全部可能性，这个系统是不可观测的！就是是对于的信息矩阵必然存在着零空间。

也可以从下面公式51理解，不同的状态，本来应该是不同的观测，但我们这里却是相同的观测，这个系统不然不可观。

每种系统都对应有着不可观的维度！

4.2.2 单目SLAM系统的可观性

单目SLAM姿态不可观是因为其绝对坐标系位置！我们给下面的旋转平移同时乘以一个变换矩阵T，它们之间的关系不会发生改变！我们不知道它具体再那个地方，也就是绝对坐标系未知！尺度就更好理解了，单目SLAM只能估计深度-尺度，不能得到准确的尺度信息！

关于IMU由于重力存在使得roll和pitch变得可观----以一个刚体为例，它垂直地面时候，重力垂直向下，没有其它方向的分力，但是它roll和pitch就会使得其它方向存在重力的分力！但是对于偏航角yaw来说，不管怎么转，重力都不会再这里有分力的存在，所以yaw也是不可观的！还有IMU是有尺度的，因为其可以测量加速度，就知道速度以及位移，只不过可能单独使用没那么准确

4.3 FEJ算法

  滑动窗口算法中，对于同一个变量，不同残差对其计算雅克比矩阵时线性化点可能不一致，导致信息矩阵可以分成两部分，相当于在信息矩阵中多加了一些信息，使得其零空间出现了变化。

  FEJ 算法：不同残差对同一个状态求雅克比时，线性化点必须一致。这样就能避免零空间退化而使得不可观变量变得可观。

注意VINS里面没有使用

5 滑动窗口算法中关键问题

如何更新先验残差？

目的：虽然先验信息矩阵固定不变，但随着迭代的推进，变量被不断优化，先验残差需要跟随变化。否则，求解系统可能奔溃。

——直白点说，如果残差不变化，意味着优化变量虽然在变，但对系统没啥效果，我们本来的目的就是找到一个让残差不断变小的方向去优化变量，但此时算法可能找到方向了，但残差不发生变化，导致算法认为方向错误，这样系统可能会崩溃！

——在滑动窗口算法中，当前还在窗口内的变量其残差肯定是可以计算的，但之前的信息、状态已经被丢弃了，也就是带来的先验残差应该如何更新？

$$\left[\begin{array}{cc}I& -H_{pm}{H}_{mm}^{-1}\\ 0& I\end{array}\right]\left[\begin{array}{cc}{H}_{pp}& H_{pm}\\ H_{mp}& H_{mm}\end{array}\right]\left[\begin{array}{c}\Delta x_{\mathrm{p}}^{\ast }\\ \Delta x_c^{\ast }\end{array}\right]=\left[\begin{array}{cc}I& -H_{pm}{H}_{mm}^{-1}\\ 0& I\end{array}\right]\left[\begin{array}{c}{b}_{pp}\\ b_{mm}\end{array}\right].$$

$$\left[\begin{array}{cc}\left(H_{pp}-H_{pm}{H}_{mm}^{-1}{H}_{mp}\right)& 0\\ H_{mp}& H_{mm}\end{array}\right]\left[\begin{array}{c}\Delta x_{\mathrm{p}}^{\ast }\\ \Delta x_c^{\ast }\end{array}\right]=\left[\begin{array}{c}{b}_{pp}-H_{pm}{H}_{mm}^{-1}{b}_{mm}\\ b_{mm}\end{array}\right]$$

​ 就是要注意到不仅信息矩阵中添加了之前变量的先验信息，残差中也带来了先验残差！

方法：先验残差的变化可以使用一阶泰勒近似。这样不断更新残差，使其呈现下降趋势

$$\begin{array}{rl}{\mathbf{b}}_{\mathrm{p}}^{\prime }& ={\mathbf{b}}_{\mathbf{p}}+\frac{\partial {\mathbf{b}}_{\mathbf{p}}}{\partial {\mathbf{x}}_{\mathbf{p}}}\delta {\mathbf{x}}_{\mathbf{p}}\\ & ={\mathbf{b}}_{\mathrm{p}}+\frac{\partial \left(-{\mathbf{J}}^{\top }{\mathbf{\Sigma }}^{-1}\mathbf{r}\right)}{\partial {\mathbf{x}}_{\mathrm{p}}}\delta {\mathbf{x}}_{\mathrm{p}}\\ & ={\mathbf{b}}_{\mathbf{p}}-{\mathbf{\Lambda }}_{\mathbf{p}}\delta {\mathbf{x}}_{\mathbf{p}}\end{array}$$

6 作业

6.1

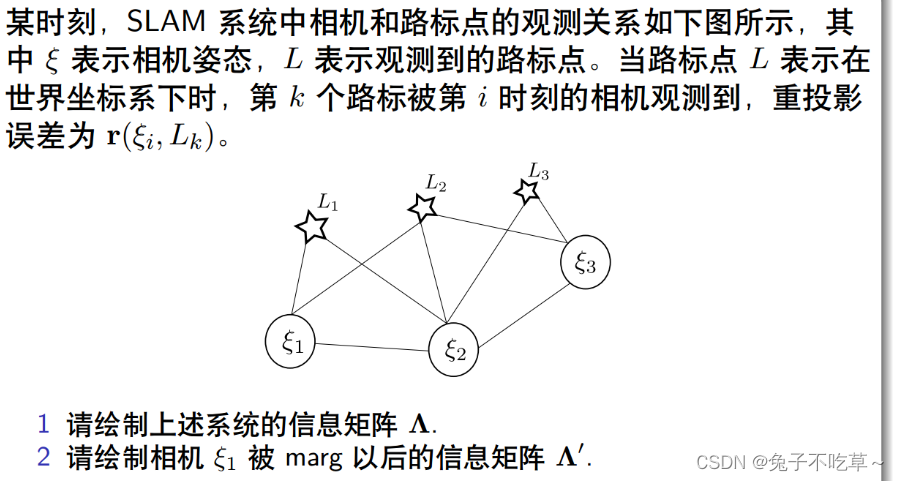
懒得画了，参考别人

6.2 补充程序

这里其实要证明的一件事情就是单目BA的信息矩阵H，其奇异值最后7维接近于0，也就是说明有7个维度是不可以观测的，零空间维度是7。----对应6自由度姿态+尺度

  奇异值分解（Singular Value Decomposition，SVD）可以用来分析矩阵的可观性和不可观性。

  对于一个线性系统，如果它的状态完全可以通过观测得到，那么称该系统是可观的。反之，如果存在一些状态无法被观测到，那么称该系统是不可观的。

  假设我们有一个线性系统的状态方程为x_dot = Ax + Bu，其中x表示状态向量，u表示控制输入。如果我们可以通过观测某些输出y来确定状态x，则该系统是可观的。这意味着我们可以找到一个观测矩阵C，使得y = Cx。

  现在，假设我们想要确定一个线性系统的可观性。我们可以使用奇异值分解来实现。具体地说，我们可以对矩阵C进行奇异值分解。如果矩阵C的奇异值中存在为0的奇异值，那么该系统是不可观的。反之，如果所有的奇异值都大于0，那么该系统是可观的。

  因此，奇异值分解可以用来分析线性系统的可观性和不可观性。

还有那个海瑟矩阵该怎么填

注意单目SLAM中只有对位姿和路标点的雅可比，所以就可以下为下面的形式----还有它这里相当于假设每个位姿都观测到所有的路标点

H.block(i*6,i*6,6,6) += jacobian_Ti.transpose() * jacobian_Ti;
/// 请补充完整作业信息矩阵块的计算
H.block(j*3 + 6*poseNums,j*3 + 6*poseNums,3,3) +=jacobian_Pj.transpose() * jacobian_Pj;
H.block(i*6,j*3 + 6*poseNums, 6,3) += jacobian_Ti.transpose() * jacobian_Pj;
H.block(j*3 + 6*poseNums,i*6 , 3,6) += jacobian_Pj.transpose() * jacobian_Ti;

HΔx=0实际验证了这件事情----奇异值从大到小进行排序！

     147.51129.146108.42...0.005023410.00484340.004510830.00426270.003862230.003516510.003029630.002534590.002302460.00172459
0.000422374
3.21708e-17
2.06732e-17
1.43188e-17
7.66992e-18
6.08423e-18
6.05715e-18
3.94363e-18

程序

#include <iostream>
#include <vector>
#include <random>  
#include <Eigen/Core>
#include <Eigen/Geometry>
#include <Eigen/Eigenvalues>struct Pose
{Pose(Eigen::Matrix3d R, Eigen::Vector3d t):Rwc(R),qwc(R),twc(t) {};Eigen::Matrix3d Rwc;Eigen::Quaterniond qwc;Eigen::Vector3d twc;
};int main()
{int featureNums = 20;       // 路标点数int poseNums = 10;          // 姿态数量// 对位姿的雅可比分为旋转和平移两部分，单目SLAM中是一个2*6的矩阵；对于路标点的雅可比是一个2*3的矩阵int diem = poseNums * 6 + featureNums * 3;      // 10*6+20*3=120double fx = 1.;     // 焦距f分别在x,y轴方向等价的像素个数double fy = 1.;Eigen::MatrixXd H(diem,diem);   // H = J^T*JH.setZero();std::vector<Pose> camera_pose;double radius = 8;// 这里就是模拟了10个姿态，旋转范围绕z轴旋转90°，平均到10个姿态里面，旋转矩阵Rwc,典型的绕动轴旋转。// 平移量xy肯定是负的，画个图就能看出来。以最开始为世界系，后面旋转为相机系for(int n = 0; n < poseNums; ++n ) {double theta = n * 2 * M_PI / ( poseNums * 4); // 1/4 圆弧// 绕 z轴 旋转Eigen::Matrix3d R;R = Eigen::AngleAxisd(theta, Eigen::Vector3d::UnitZ());// 每次还要进行一定量xyz上面的平移,Eigen::Vector3d t = Eigen::Vector3d(radius * cos(theta) - radius, radius * sin(theta), 1 * sin(2 * theta));camera_pose.push_back(Pose(R,t));}// 随机数生成20个三维特征点std::default_random_engine generator;std::vector<Eigen::Vector3d> points;for(int j = 0; j < featureNums; ++j){std::uniform_real_distribution<double> xy_rand(-4, 4.0);std::uniform_real_distribution<double> z_rand(8., 10.);double tx = xy_rand(generator);double ty = xy_rand(generator);double tz = z_rand(generator);Eigen::Vector3d Pw(tx, ty, tz);points.push_back(Pw);for (int i = 0; i < poseNums; ++i) {Eigen::Matrix3d Rcw = camera_pose[i].Rwc.transpose();Eigen::Vector3d Pc = Rcw * (Pw - camera_pose[i].twc);double x = Pc.x();double y = Pc.y();double z = Pc.z();double z_2 = z * z;Eigen::Matrix<double,2,3> jacobian_uv_Pc;jacobian_uv_Pc<< fx/z, 0 , -x * fx/z_2,0, fy/z, -y * fy/z_2;Eigen::Matrix<double,2,3> jacobian_Pj = jacobian_uv_Pc * Rcw;Eigen::Matrix<double,2,6> jacobian_Ti;jacobian_Ti << -x* y * fx/z_2, (1+ x*x/z_2)*fx, -y/z*fx, fx/z, 0 , -x * fx/z_2,-(1+y*y/z_2)*fy, x*y/z_2 * fy, x/z * fy, 0,fy/z, -y * fy/z_2;H.block(i*6,i*6,6,6) += jacobian_Ti.transpose() * jacobian_Ti;/// 请补充完整作业信息矩阵块的计算H.block(j*3 + 6*poseNums,j*3 + 6*poseNums,3,3) +=jacobian_Pj.transpose() * jacobian_Pj;H.block(i*6,j*3 + 6*poseNums, 6,3) += jacobian_Ti.transpose() * jacobian_Pj;H.block(j*3 + 6*poseNums,i*6 , 3,6) += jacobian_Pj.transpose() * jacobian_Ti;}}//    std::cout << H << std::endl;
//    Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes(H);
//    std::cout << saes.eigenvalues() <<std::endl;// 奇异值分解Eigen::JacobiSVD<Eigen::MatrixXd> svd(H, Eigen::ComputeThinU | Eigen::ComputeThinV);// 调用svd对象的singularValues()成员函数，矩阵H的奇异值std::cout << svd.singularValues() <<std::endl;// 于一个矩阵而言，它的奇异值越大，表示它的特征、结构和变换等信息越重要。// 而奇异值越小，则说明这部分信息对矩阵的影响越小return 0;
}

这篇关于VIO第4讲：基于滑动窗口法的vio系统可观性与一致性的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---