旷视low-level系列（三）：（NAFNet）Simple Baselines for Image Restoration

本文主要是介绍旷视low-level系列（三）：（NAFNet）Simple Baselines for Image Restoration，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目：Simple Baselines for Image Restoration
单位：旷视
收录：ECCV2022
论文：https://arxiv.org/abs/2204.04676
代码：https://github.com/megvii-research/NAFNet

1. Motivation

图像恢复领域的SOTA方法性能越来越高，但模型复杂度也随之水涨船高，对实时性要求较高的应用场景而言落地相当困难。对于业务导向的研究，自然而然就会将研究重点转向以较低的复杂度实现SOTA性能。在该篇论文中，旷视的研究员们提出了一个用于图像恢复任务的简单基线，性能超过SOTA方法，并且计算效率更高。

2. Contributions

• 通过对SOTA方法进行分解并提取它们的基本组件，形成了一个系统复杂度较低的基线，性能上超过以前的SOTA方法，并具有较低的计算成本；
• 通过去除或替换非线性激活函数进一步简化了基线，并提出了一个非线性无激活的网络–NAFNet，性能上匹配甚至超过基线；首次证明了非线性激活函数可能不是SOTA模型所必要的网络组件。
  

3. Methods

为了便于讨论，作者将模型的系统复杂度分解为块间复杂度（inter-block complexity）和块内复杂度（intra-block complexity），其中，块间复杂度指的是block之间的各种连接方式的复杂程度，例如下图展示的(a)多阶段架构和(b)多尺度融合架构，块内复杂度指的是block内部组件的复杂程度。为了降低块间复杂度，作者采用了单阶段的UNet，并着重研究如何降低块内复杂度。

Fig.1

如何设计block的内部结构使其具有较低复杂度呢？作者的思路大概如下：先设计一个简单的plain block，然后参考SOTA模型中成熟且切实有效的模块，在plain block中逐一添加或替换得到baseline block，并通过消融实验验证性能是否有提升；最后在保证性能不损失的情况下进一步简化结构，以最大程度地降低块内复杂度。

Fig.2

plain block
考虑到transformer架构对于部分SOTA方法来说不是必要的，并且其计算复杂度较高，与simple baseline的目标相悖，因此设计plain block的内部结构时抛弃了self-attention这样的复杂结构，只考虑使用卷积、激活和shortcut等简单组件，排列顺序参考Restormer中的block。

baseline block
基于plain block，从normalization，activation和attention三个方面进行改进。

• normalization
  BN不适用于low-level视觉任务应该是一种共识，网络中加入BN会导致性能下降。

BN导致性能下降的原因可能有：
1）小的batch-size带来不稳定的统计；
2）不同于high-level task倾向于寻找一致性表示，底层视觉的任务与之相反，往往是倾向于学习图片特定性以增强细节的恢复效果（比如之前有人通过捕获图像分布的sigma以增强边缘区域的效果），batchNorm由于是batch内做attention，其实很容易将其他图片的信息引入，忽略了恢复图像的特定信息，导致性能下降。

考虑到LN在transformer和众多SOTA图像恢复方法中广泛使用，作者推测LN是达到SOTA性能的一个必要组件，因此在plain block中添加了LN。由于LN的存在，即使学习率增加10倍训练过程仍然稳定，并且大的学习率能够带来显著的性能增益：SIDD+0.44dB，GoPro+3.39dB。

• activation
  ReLU被广泛应用于计算机视觉任务中，但是目前的SOTA方法中逐渐倾向于使用GELU（高斯误差线性单元激活函数）代替ReLU，例如transformer中主要使用GELU激活函数，因此作者也将plain block中的ReLU替换为GELU。替换结果：SIDD-0.02dB，GoPro+0.21dB，去噪性能相当，但是去模糊有提升，因此选择使用GELU作为激活函数。
• attention
  low-level任务的图像输入分辨率一般都很高，例如常用的1080p，self-attention的计算复杂度随着空间分辨率的增加而二次增长这一缺陷导致其实用性大大降低。Uformer中提出只在固定大小的窗口中应用self-attention以降低计算量，但缺点是丢失了全局信息；Restormer中提出的Multi-Dconv Head Transposed Attention模块将空间attention修改为通道attention，通过计算通道上的注意力来隐式编码全局上下文信息，可以视为SENet中所提出的通道注意力的一种变体。受Restormer启发，作者认为baseline中的通道注意力只需要满足两点要求：1）计算效率高；2）能够捕获全局信息。SENet中提出的通道注意力就能满足要求，将其添加到plain block中后，SIDD+0.14dB，GoPro+0.24dB。

经过normalization，activation和attention这三个方面的改进后，形成了Fig.2c所示的baseline block。

NAFNet's block
baseline block的结构已经很简单了，但是论文中进一步提出问题：是否有可能在确保简单的同时进一步提高性能？它能在不造成性能损失的情况下更简单吗？作者们试图通过寻找一些SOTA方法的共性来回答这些问题，发现SOTA方法中大多采用了门控线性单元（GLU），这意味着GLU可能是一个有效组件。

GLU的形式如下：

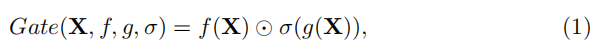
其中$X$表示特征图，$f$和$g$为线性变换器，$\sigma$为非线性激活函数，如Sigmoid，⊙表示元素级乘法。添加GLU到baseline中可能会提高性能，但块内的复杂性也在增加，与“更简单”的目标相悖。为了解决该问题，作者重新审视了baseline中的GELU，发现GLU与GELU在形式上存在可转换性。GELU的形式如下：

不难看出，当GLU中的$f$和$g$均为identity，$\sigma$为$\Phi$时，GLU与GELU是等价的。另外，GLU中的非线性不是仅由$\sigma$决定的，在移除$\sigma$的情况下，$f(X)\cdot g(X)$也能引入非线性。基于以上分析，作者提出了一种GLU的变体，直接在通道维度中将特征图分成两部分，并将它们相乘，形式如下：

Fig.3

将baseline block中的GELU替换为Simple Gate后，SIDD+0.08dB，GoPro+0.41dB，该结果表明在图像恢复任务中GELU可以被Simple Gate所取代。

至此，网络中只剩下少数几种非线性激活：通道注意模块中的Sigmoid和ReLU。图穷匕见呀，作者就是想将网络中的非线性激活全部干掉，设计首个无需非线性激活的图像恢复SOTA模型！

SENet中提出的channel attention的形式如下：

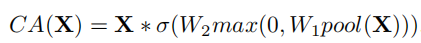
如果将attention的生成过程用函数表示，CA(x)可以简化为：

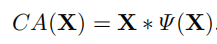
突然发现和GLU的形式惊人的相似呀，作者认为可以将channel attention视为GLU的一种特殊情况，通过保留channel attention的聚合全局信息和通道信息交互这两个最重要的作用，提出了simplified channel attention（SCA）：


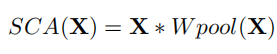
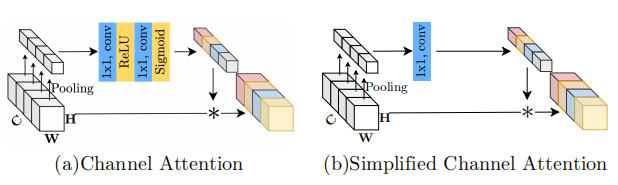
虽然SCA相比CA在形式上更为简单，但是性能没有损失，SIDD+0.03dB，GoPro+0.09dB。

由于最终的网络中没有非线性激活函数，作者将其命名为：Nonlinear Activation Free Network，NAFNet。

这篇关于旷视low-level系列（三）：（NAFNet）Simple Baselines for Image Restoration的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---