本文主要是介绍LAPACK xgeqr2.f 算法总结推导,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
以 DGEQR2 函数为例,其分为两步:
先计算Householder vector,调用了 DLARFG( )
然后实施了Householder 变换,调用了 DLARF( )
接下来先分析DLARFG( )的算法
源代码如下:
*> \brief \b DLARFG generates an elementary reflector (Householder matrix).
*
* =========== DOCUMENTATION ===========
*
* Online html documentation available at
* http://www.netlib.org/lapack/explore-html/
*
*> \htmlonly
*> Download DLARFG + dependencies
*> <a href="http://www.netlib.org/cgi-bin/netlibfiles.tgz?format=tgz&filename=/lapack/lapack_routine/dlarfg.f">
*> [TGZ]</a>
*> <a href="http://www.netlib.org/cgi-bin/netlibfiles.zip?format=zip&filename=/lapack/lapack_routine/dlarfg.f">
*> [ZIP]</a>
*> <a href="http://www.netlib.org/cgi-bin/netlibfiles.txt?format=txt&filename=/lapack/lapack_routine/dlarfg.f">
*> [TXT]</a>
*> \endhtmlonly
*
* Definition:
* ===========
*
* SUBROUTINE DLARFG( N, ALPHA, X, INCX, TAU )
*
* .. Scalar Arguments ..
* INTEGER INCX, N
* DOUBLE PRECISION ALPHA, TAU
* ..
* .. Array Arguments ..
* DOUBLE PRECISION X( * )
* ..
*
*
*> \par Purpose:
* =============
*>
*> \verbatim
*>
*> DLARFG generates a real elementary reflector H of order n, such
*> that
*>
*> H * ( alpha ) = ( beta ), H**T * H = I.
*> ( x ) ( 0 )
*>
*> where alpha and beta are scalars, and x is an (n-1)-element real
*> vector. H is represented in the form
*>
*> H = I - tau * ( 1 ) * ( 1 v**T ) ,
*> ( v )
*>
*> where tau is a real scalar and v is a real (n-1)-element
*> vector.
*>
*> If the elements of x are all zero, then tau = 0 and H is taken to be
*> the unit matrix.
*>
*> Otherwise 1 <= tau <= 2.
*> \endverbatim
*
* Arguments:
* ==========
*
*> \param[in] N
*> \verbatim
*> N is INTEGER
*> The order of the elementary reflector.
*> \endverbatim
*>
*> \param[in,out] ALPHA
*> \verbatim
*> ALPHA is DOUBLE PRECISION
*> On entry, the value alpha.
*> On exit, it is overwritten with the value beta.
*> \endverbatim
*>
*> \param[in,out] X
*> \verbatim
*> X is DOUBLE PRECISION array, dimension
*> (1+(N-2)*abs(INCX))
*> On entry, the vector x.
*> On exit, it is overwritten with the vector v.
*> \endverbatim
*>
*> \param[in] INCX
*> \verbatim
*> INCX is INTEGER
*> The increment between elements of X. INCX > 0.
*> \endverbatim
*>
*> \param[out] TAU
*> \verbatim
*> TAU is DOUBLE PRECISION
*> The value tau.
*> \endverbatim
*
* Authors:
* ========
*
*> \author Univ. of Tennessee
*> \author Univ. of California Berkeley
*> \author Univ. of Colorado Denver
*> \author NAG Ltd.
*
*> \ingroup doubleOTHERauxiliary
*
* =====================================================================SUBROUTINE DLARFG( N, ALPHA, X, INCX, TAU )
*
* -- LAPACK auxiliary routine --
* -- LAPACK is a software package provided by Univ. of Tennessee, --
* -- Univ. of California Berkeley, Univ. of Colorado Denver and NAG Ltd..--
*
* .. Scalar Arguments ..INTEGER INCX, NDOUBLE PRECISION ALPHA, TAU
* ..
* .. Array Arguments ..DOUBLE PRECISION X( * )
* ..
*
* =====================================================================
*
* .. Parameters ..DOUBLE PRECISION ONE, ZEROPARAMETER ( ONE = 1.0D+0, ZERO = 0.0D+0 )
* ..
* .. Local Scalars ..INTEGER J, KNTDOUBLE PRECISION BETA, RSAFMN, SAFMIN, XNORM
* ..
* .. External Functions ..DOUBLE PRECISION DLAMCH, DLAPY2, DNRM2EXTERNAL DLAMCH, DLAPY2, DNRM2
* ..
* .. Intrinsic Functions ..INTRINSIC ABS, SIGN
* ..
* .. External Subroutines ..EXTERNAL DSCAL
* ..
* .. Executable Statements ..
*IF( N.LE.1 ) THENTAU = ZERORETURNEND IF
*XNORM = DNRM2( N-1, X, INCX )
*IF( XNORM.EQ.ZERO ) THEN
*
* H = I
*TAU = ZEROELSE
*
* general case
*BETA = -SIGN( DLAPY2( ALPHA, XNORM ), ALPHA )SAFMIN = DLAMCH( 'S' ) / DLAMCH( 'E' )KNT = 0IF( ABS( BETA ).LT.SAFMIN ) THEN
*
* XNORM, BETA may be inaccurate; scale X and recompute them
*RSAFMN = ONE / SAFMIN10 CONTINUEKNT = KNT + 1CALL DSCAL( N-1, RSAFMN, X, INCX )BETA = BETA*RSAFMNALPHA = ALPHA*RSAFMNIF( (ABS( BETA ).LT.SAFMIN) .AND. (KNT .LT. 20) )$ GO TO 10
*
* New BETA is at most 1, at least SAFMIN
*XNORM = DNRM2( N-1, X, INCX )BETA = -SIGN( DLAPY2( ALPHA, XNORM ), ALPHA )END IFTAU = ( BETA-ALPHA ) / BETACALL DSCAL( N-1, ONE / ( ALPHA-BETA ), X, INCX )
*
* If ALPHA is subnormal, it may lose relative accuracy
*DO 20 J = 1, KNTBETA = BETA*SAFMIN20 CONTINUEALPHA = BETAEND IF
*RETURN
*
* End of DLARFG
*END
摘取将其常规运算部分归结如下,并加入了注释:
* 计算(x_1, x_2, ..., x_n-1)的模长norm,即 sqrt(x1*x1 + x2*x2 + ... xn-1*xn-1)XNORM = DNRM2( N-1, X, INCX )* 计算(x_0, x_1, x_2, ..., x_n-1)的模长,并且取符号正好与 x0 == ALPHA 的符号相反
* 其中的 DLAPY2(s, t) = sqrt(s*s + t*t);BETA = -SIGN( DLAPY2( ALPHA, XNORM ), ALPHA )* 按照Householder常规, TAU = 2.0/X^T*X = 2.0/( 1.0*1.0 + (x1/(ALPHA-BETA))**2 + (x2/(ALPHA-BETA))**2 + ... + (x_n-1/(ALPHA-BETA))**2 ) 然后就可以推导出 TAU = (BETA-ALPHA)/BETATAU = ( BETA-ALPHA ) / BETA
* 对 X 做缩放, st. 理念中的 X(0) == 1.0 ,但是下面语句中的 X 中只包含了从X(1) 到 X(n-1)CALL DSCAL( N-1, ONE / ( ALPHA-BETA ), X, INCX )
* ALPHA 即 Y(0) = (Px)(0) = ((I - beta*V*V^T)x)(0) = Y(0)ALPHA = BETA
至此,这个Householder vector 就计算出来了。
效果相当于给定
计算出其Householder vector:
同时计算出了 Y=PX:
其中 存储在变量
中了。
然后又利用 DLARF( )将Householder vector 应用到了 A矩阵的剩余部分。
接下来分析 DLARF( ) 的算法实现。

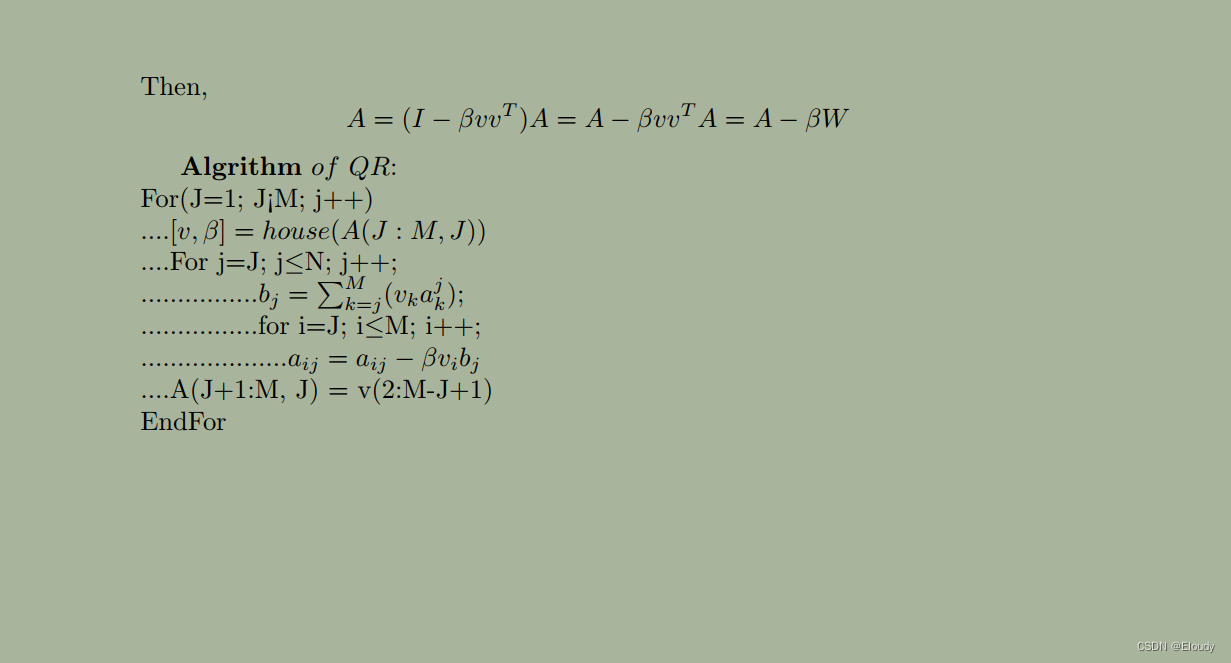
\documentclass{article}
\title{House}\begin{document}
\maketitle
After we calculated $v$ and $\beta$:
$$[v,\beta]= house(A(j:m, j))$$
we should update A by:
$$A = (I-\beta vv^T)A$$Let
$$v=
\left[\begin{array}{c}v_1\\v_2\\\vdots\\v_m\end{array}
\right]
$$
then,
$$vv^T=
\left[\begin{array}{cccc}v_1v_1 & v_1v_2 & \cdots & v_1v_m\\v_2v_1 & v_2v_2 & \cdots & v_2v_m\\\vdots & \vdots & \ddots & \vdots\\v_mv_1 & v_mv_2 & \cdots & v_mv_m\end{array}
\right]
$$As
$$
A = (I-\beta vv^T)A=A - \beta vv^TA
$$
to calculat $(vv^TA)$,
$$
vv^TA=v(v^TA)=
\left[\begin{array}{c}v_1\\v_2\\\vdots\\v_m\end{array}
\right]
\left[ \sum_{k=1}^m(v_ka_{k1}) \,\, \sum_{k=1}^m(v_ka_{k2}) \cdots \sum_{k=1}^m(v_ka_{kn})\right]
$$Let $b_j=\sum_{k=1}^m(v_ka_{kj})$$$
W=vv^TA=v(v^TA)=
\left[\begin{array}{c}v_1\\v_2\\\vdots\\v_m\end{array}
\right]
\left[b_1\,\,b_2 \cdots b_n\right]
=
\left[\begin{array}{cccc}v_1b_1 & v_1b_2 & \cdots & v_1b_n\\v_2b_1 & v_2b_2 & \cdots & v_2b_n\\\vdots & \vdots & \ddots & \vdots\\v_mb_1 & v_mb_2 & \cdots & v_mb_n\\\end{array}
\right]
$$
Then,
$$
A=(I-\beta vv^T)A = A-\beta vv^TA = A-\beta W
$$$\mathbf{Algrithm}\,\, of\,\, QR$:\\
For(J=1; J<M; j++)\\
....$[v, \beta] = house(A(J:M, J))$\\
....For j=J; j$\le$N; j++;\\
................$b_j=\sum_{k=j}^M(v_ka_k^j)$;\\
................for i=J; i$\le$M; i++;\\
....................$a_{ij} = a_{ij}-\beta v_ib_j$\\
....A(J+1:M, J) = v(2:M-J+1)\\
EndFor
\end{document}
这篇关于LAPACK xgeqr2.f 算法总结推导的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







