机器学习Day2-机器学习算法过程没有免费午餐定理

一、机器学习算法过程

大部分人认为随着大数据和深度学习的发展，只要将网上的数据随意的放进模型中，就可以实现了，其实这是一个错误的观点【笔者一开始也是这样想的】，确实有时候能得到正确的结论，但是大部分是错的

1.特征提取【Feature Extraction】

• 通过训练样本获得的，对机器学习任务有帮助的多维度数据

• 机器学习的重点不是为了研究如何去提取特征

• 机器学习的重点：假设在已经提取好特征的前提下，去如何构造算法获得更好的性能

• 当然也不是说提取特征不重要，如果我们提取了好的特征，那么我们机器就能获得不错的性能，相反，如果我们提取的特征很差，即使我们有非常大的机器学习的算法，也是不可能获得好的性能的，

2.为什么不以特征提取为重点？

这是因为不同的任务提取特征的方式是不同的，针对不同的煤质不同的任务，提取特征的方式是千变万化的，【例如语音、图像、视频等】，要是以此为重点，即使花费几门课也讲不完，因此机器学习注重于在假设已经获得特征的前提下，去研究合理的算法，去让学习系统获得更好的性能。

3.特征选择【Feature Selection】

1. • 例子

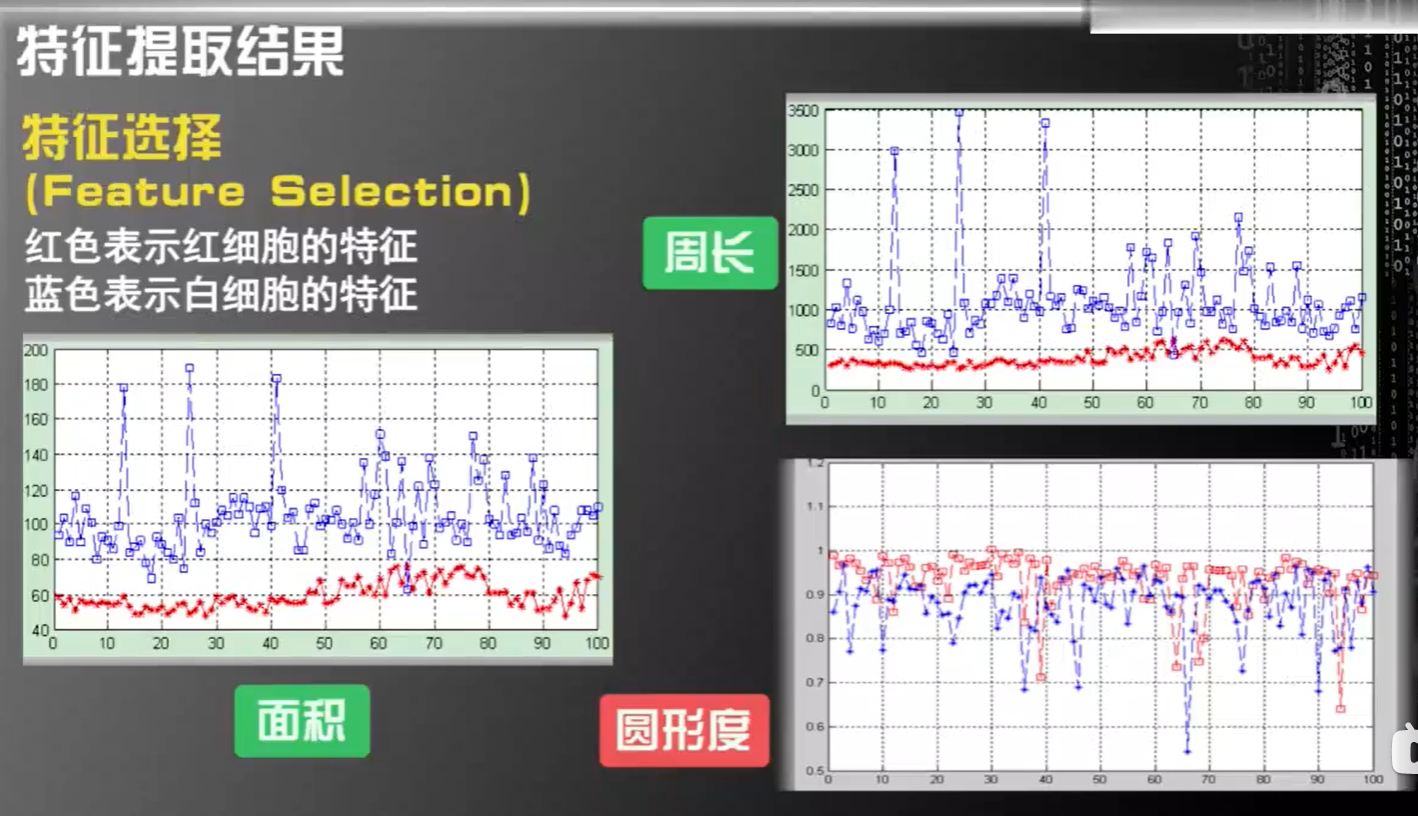
• 我们可以发现，白细胞和红细胞在周长和面积这两个特征中的重合度很少，而其圆形度，虽然红细胞在白细胞的上方,但是重合度很大，因此如果我们采用圆形度作为区分白细胞和红细胞的特征，那么其识别率并不会很高，这两种在其他方面的重合度也很大，因此，我们会采取重合度少的周长和面积，作为区分白细胞和红细胞的特征，以此来构建机器学习的系统。

4.算法构建

那么如何以这两种特征来构建算法呢？他们采取了支持向量机【Support Vector Machine】，一共有三种内核，可以把下列的三种看做三种算法模式

1. 线性内核

2. 多项式内核

3. 高斯径向基函数核

5.特征空间【Feature Space】

• 基于上述两种特征，研究者将白细胞和红细胞画到了同一个二维空间中，其中横坐标代表面积，纵坐标代表周长，以此去描点，并做了一定程度的归一，将这两个特征的值归一化到【-1,1】,在这个例子中，我们把这个二维空间成为特征空间【Feature Space】，如果在其他方面，有多个特征，那么特征空间可以是多维的。

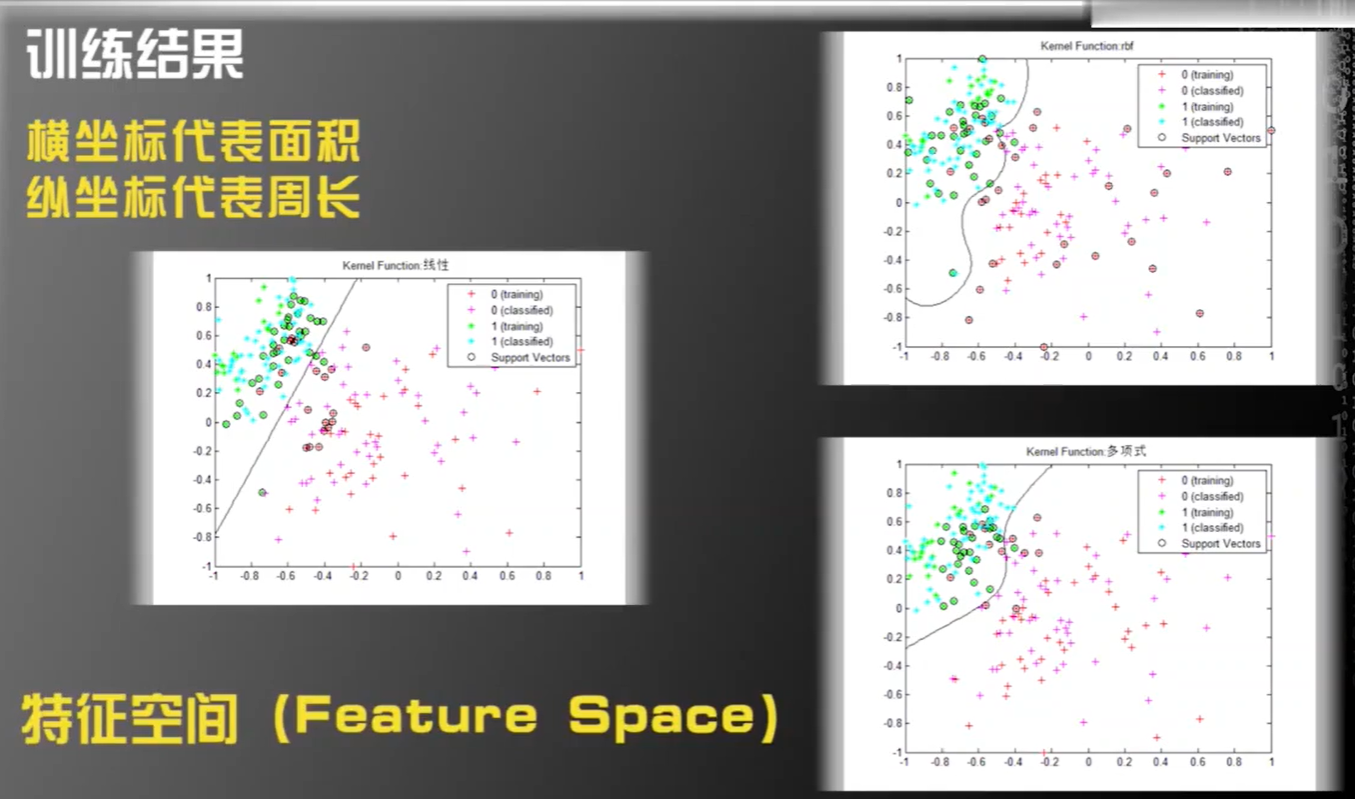
• 那么基于之前提到的三种算法，我们在图纸上画出了三条不同的分界线，一旦我们画出这一线条，那么就代表我们机器学习的过程就已经结束了。

• 为何这么说呢，例如，这时候来了一个新的样本，我们计算它的周长和面积，再进行一定程度上的归一，再画到这张图上，看是在这一条线的那一侧，就可以进行分类了

• 在此有两个概念【维度和标准】，【维度】有人说，我一眼就能画出这条线，那是因为这里的维度是二维的，那么如果，维度是上万维，那么你还能看出来吗？人眼对于多维是缺乏想象力的。【标准】上述基于三种算法，画出的线，对于某些区域的划分是不一样的，例如，第二张图片和第三张图片的左下侧

• 那么哪种算法更好呢，我们针对于不同的情况，需要去采取不同的方法，这个没有绝对意义的好和坏的标准，因为我们采取的数据是有限的，当然我们也不可能穷尽所有的样本数据，如何针对不同的应用场景，选择不同的机器学习算法，构造新的机器学习算法，解决目前无法解决的应用场景，这是一个理论和实践的科学过程

二、没有免费午餐定理【No Free Lunch Theorem】

• 针对于之前提出的哪种算法更好，我们在这给出一个初步的回答，1995年，D.H.Wolpert等人提出了没有免费午餐定理【No Free Lunch Theorem】

• 定理概述：任何一个预测函数，如果在一些训练样本上表现好，那么必然在另一些训练样本表现不好，如果不对数据在特征空间的先验分布有一定的假设，那么表现好与表现不好的情况一样多，因此不存在，在任何情况下都是非常完美的机器学习算法

• 对于先验分布概率，有如下要求

那么，这一假设有道理吗？有道理，但是也可能出错

基于没有免费午餐定理，我们如果不对特征空间的先验分布有要求，那么所以算法的表现概率都是一样的，我们不能片面的去夸大这一定理的作用，从而对开发新的算法丧失信心，但是我们要时刻牢记这一定理的提醒，

因此，再好的算法，也会有犯错的可能，【没有免费午餐定理】告诉我们，没有放之四海皆准的算法，没有人能知道先验样本的假设【就像，明天的太阳一定会升起吗】