本文主要是介绍《DSAA》 10.1.2 Huffman 编码,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Huffman 编码是高大上的压缩算法,基本原理却出乎意料地简单,大致可分为以下步:
1)扫描压缩的缓存或文件,搜集每个字符出现的频率
2)根据扫描结果构造Huffman 树,得到每个字符的 Huffman 代码
3)用 Huffman 代码重新对缓存或文件进行编码
这里关键是第二步Huffman 树的构造,Huffman 树是一颗满的二叉树,用一个值为0的bit 代表树根,每下一层增加一个bit,如果是左儿子该bit值为0,右儿子该bit为1。字符都放在树叶上,频率越高的字符所在的树叶离树根越近,这也就意味着其代码越短,注意这些字符代码的长度不同并不要紧,只要没有字符代码是别的字符代码的前缀即可,这也是为什么所有字符不能放在非树叶节点上。
原理搞清后,具体实现就比较简单(同时也很巧妙)了:
1)为每个字符创建一颗 Huffman 树,一颗树的权就是该字符的频率,然后把这些树全部插入一个优先队列(我用的是一个二叉堆)
2)出队具有最小权的两颗树,合并之,使新树的权等于原来两颗树的权之和,然后将新树插回优先队列
3)反复执行第二步,直到只剩下一棵树,这就是最优 Huffman 编码树
4)最后计算并输出代码表
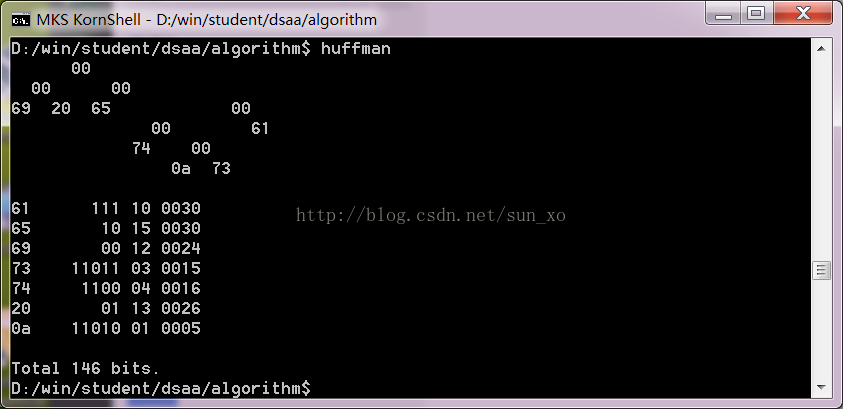
下面是对原书中示例的求解,运行结果如下 (前面是 Huffman树,后面的代码表):
这篇关于《DSAA》 10.1.2 Huffman 编码的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!