当初自学围棋的时候背过一些定式，一般定式都比较容易，从开始到结束用不了几个回合。直到有一天遇到了像妖刀，大雪崩，大斜这样的大型定式，变化极为繁复，一个定式摆下去能占满1/4个棋盘，这个要掌握就非常困难了。 如果把算法类比为围棋的布局，数据结构类比为定式的话，红黑树无疑就是一个大型定式。个人感觉它的搜索和插入什么的还算简单，而且原书也给出了实现。但难就难在删除，偏偏书里只讲了 大致思路，看着非

在许多应用中，当一个节点被访问后，马上就很可能再次被访问到，研究表明这种情况比人们预料的要频繁的多。所以伸展树的基本想法是：当一个节点被访问后，它就要通过一系列的旋转被放到根上。 自顶向下伸展树的搜索方式非常独特，它实际上是一个拆了又装的过程,这个过程被称为伸展： 最开始先新建两颗空树：L树和R树，用于缓存。在从原树自顶向下搜索时，每一次迭代都将父节点以上的部分拆除，视情况接到两旁的L

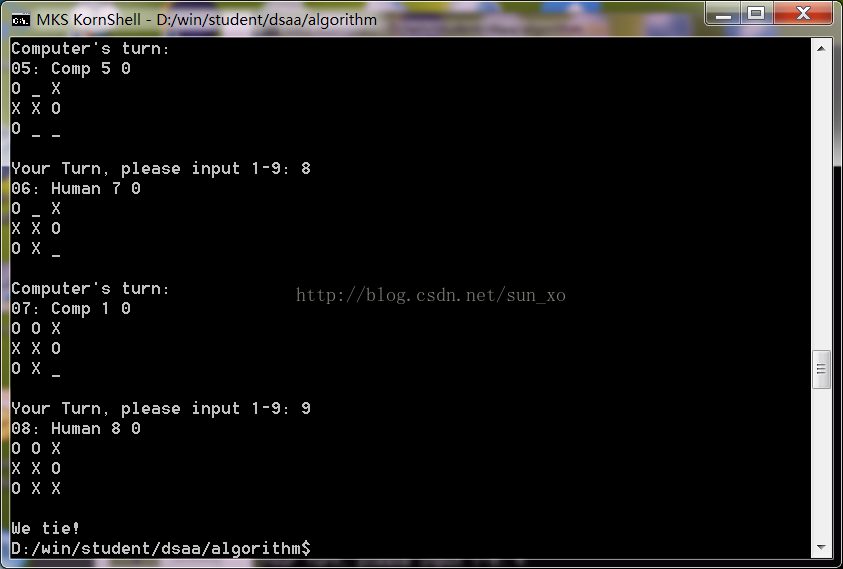
这里的博弈就是指下棋，脑海中立刻闪现出了深蓝，阿尔法狗等等光辉形象，当然那些太高大上了，超出我的智商范围，这里讨论的是最简单的三连棋（tic-tac-toe），也许基本原理和深蓝阿尔法狗都差不多吧。三连棋的玩法是：一个 3 × 3 的棋盘，一方执黑一方执白轮流落子，先在横或竖或斜三个方向上连成3个的一方获胜。 这里我们采用的策略被称为极大极小策略，它根据当前的局势给棋盘上的位置打分，如果占据某个

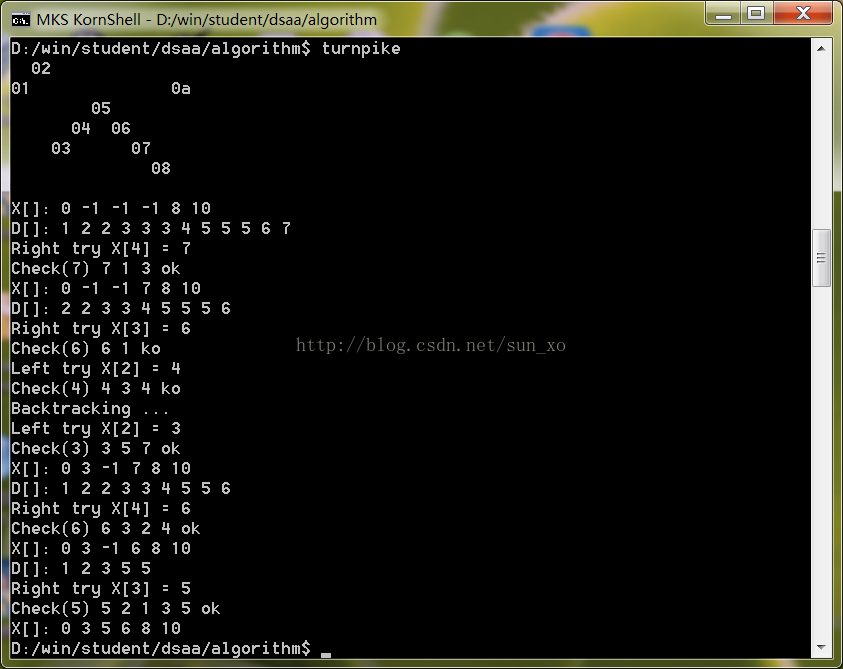
收费公路重建问题得名于对美国西海岸公路上那些收税公路出口的模拟：设一条高速公路从起点到终点之间有若干出入口（包括起点和终点），每个出入口设有一个收费站，每两个出入口的距离已知，收费站根据这些距离收费。某天不知发生了什么灾难，这些出入口及其收费站居然消失了，只有起点和各点之间的距离保存下来，现在要重建收费站，则需要求出这些出入口的位置。也就是说要根据距离的集合 D[ ]，反过来求出点的集合 X[ ]

设平面上有N个点，要找出其中两个相距最近的点，被称为最近点问题。如果简单地用蛮力解决：N个点存在N × (N - 1) / 2 条边，我们可以检查所有的边找出其中最短者，但是这样的时间界是O(N ^ 2)，比较浪费时间，还应该有更巧妙的办法，比如分治算法。 我们在平面中间画一条竖线，则点集p也被分成两半pL和pR，那么最近的一对点将会： 1）都在pL中，设其距离为dL 2）都在pR中，设其距

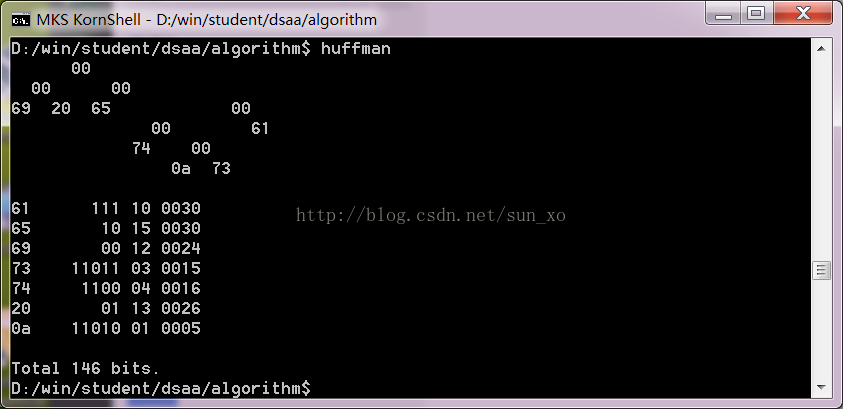
Huffman 编码是高大上的压缩算法，基本原理却出乎意料地简单，大致可分为以下步： 1）扫描压缩的缓存或文件，搜集每个字符出现的频率 2）根据扫描结果构造Huffman 树，得到每个字符的 Huffman 代码 3）用 Huffman 代码重新对缓存或文件进行编码 这里关键是第二步Huffman 树的构造，Huffman 树是一颗满的二叉树，用一个值为0的bit 代表树根，每下一层增加一

如何用最少的电线给一所房子安装电路？本质上就是如何从一个无向图中找出一颗最小生成树。一个无向图中的最小生成树由该图的那些连接所有顶点的边构成的树，且其总价值最小。 有两个解决此问题的算法：Prim 和 Kruskal，这里只讨论后者，因为它比较简明有趣。 和一般处理图的算法不同，Kruskal 实际上是在处理森林，即树的集合，开始时每个顶点是一颗单节点树，添加一条边则意味着将两颗树合并成一棵树