LeetCode 0106.从中序与后序遍历序列构造二叉树：分治（递归）——五彩斑斓的题解（若不是彩色的可以点击原文链接查看）

本文主要是介绍LeetCode 0106.从中序与后序遍历序列构造二叉树：分治（递归）——五彩斑斓的题解（若不是彩色的可以点击原文链接查看），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【LetMeFly】106.从中序与后序遍历序列构造二叉树：分治（递归）——五彩斑斓的题解（若不是彩色的可以点击原文链接查看）

力扣题目链接：https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

 

示例 1:

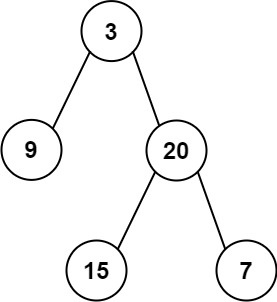
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

 

提示:

• 1 <= inorder.length <= 3000
• postorder.length == inorder.length
• -3000 <= inorder[i], postorder[i] <= 3000
• inorder 和 postorder 都由 不同 的值组成
• postorder 中每一个值都在 inorder 中
• inorder 保证是树的中序遍历
• postorder 保证是树的后序遍历

方法一：分治（递归）

类似于从前序与中序建树，我们知道：

• 中序遍历：左子树 根 右子树
• 后序遍历：左子树 右子树 根

写一个函数dfs接收中序遍历数组和后序遍历数组作为参数：

1. 根据后序遍历数组的最后一个元素为根节点建立节点
2. 找到根节点在中序遍历数组中的位置

   以此可得到左子树和右子树的长度信息

   以此可确定左子树和右子树在两个数组中的位置

3. 递归建立左子树和右子树

递归的终止条件为“中序遍历数组为空”，此时返回空节点。

Tips: 可以在预处理时建立一个哈希表，以便能快速地找到根节点在中序遍历数组中的位置。

• 时间复杂度$O(N)$，其中$N$是节点个数
• 空间复杂度$O(N)$

AC代码

C++

class Solution {
private:unordered_map<int, vector<int>::iterator> ma;TreeNode* dfs(vector<int>::iterator inLeft, vector<int>::iterator inRight, vector<int>::iterator postLeft, vector<int>::iterator postRight) {if (inLeft >= inRight) {return nullptr;}TreeNode* thisNode = new TreeNode(*(postRight - 1));vector<int>::iterator loc = ma[*(postRight - 1)];thisNode->left = dfs(inLeft, loc, postLeft, postLeft + (loc - inLeft));thisNode->right = dfs(loc + 1, inRight, postLeft + (loc - inLeft), postRight - 1);return thisNode;}
public:TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {for (vector<int>::iterator it = inorder.begin(); it != inorder.end(); it++) {ma[*it] = it;}return dfs(inorder.begin(), inorder.end(), postorder.begin(), postorder.end());}
};

Python

# from typing import List, Optional# # Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = rightclass Solution:def dfs(self, inorder: List[int], inLeft: int, inRight: int, postorder: List[int], postLeft: int, postRight: int) -> Optional[TreeNode]:if inLeft >= inRight:return NonethisNode = TreeNode(postorder[postRight - 1])loc = self.ma[postorder[postRight - 1]]thisNode.left = self.dfs(inorder, inLeft, loc, postorder, postLeft, postLeft + (loc - inLeft))thisNode.right = self.dfs(inorder, loc + 1, inRight, postorder, postLeft + (loc - inLeft), postRight - 1)return thisNodedef buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:self.ma = dict()for i in range(len(inorder)):self.ma[inorder[i]] = ireturn self.dfs(inorder, 0, len(inorder), postorder, 0, len(postorder))

同步发文于CSDN，原创不易，转载经作者同意后请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/136204741

这篇关于LeetCode 0106.从中序与后序遍历序列构造二叉树：分治（递归）——五彩斑斓的题解（若不是彩色的可以点击原文链接查看）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---