【算法与数据结构】200、695、LeetCode岛屿数量（深搜+广搜） 岛屿的最大面积

2024-02-22 09:52
文章标签 leetcode 算法 数量 数据结构 200 最大 面积 岛屿 695

本文主要是介绍【算法与数据结构】200、695、LeetCode岛屿数量（深搜+广搜） 岛屿的最大面积，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

  • 一、200、岛屿数量
    • 1.1 深度优先搜索DFS
    • 1.2 广度优先搜索BFS
  • 二、695、岛屿的最大面积
    • 2.1 深度优先搜索DFS
    • 2.2 广度优先搜索BFS
  • 三、完整代码

所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。

一、200、岛屿数量

在这里插入图片描述

1.1 深度优先搜索DFS

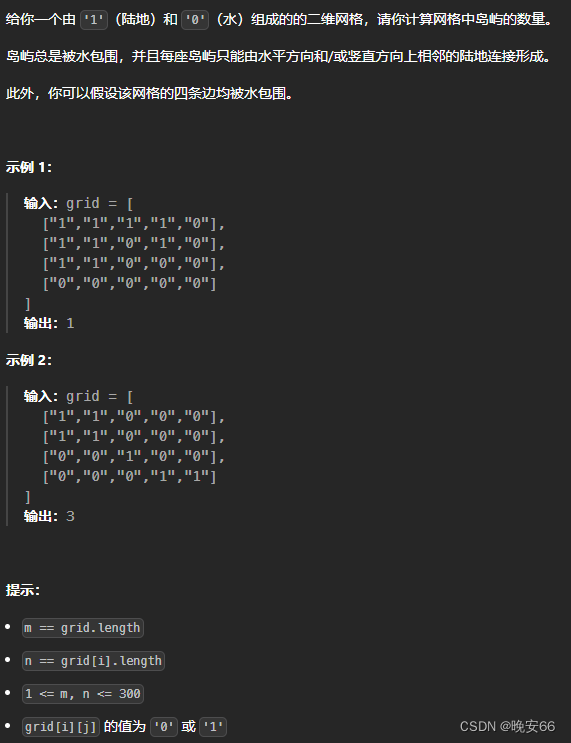
  思路分析：本题当中1代表的是陆地，0代表海洋，我们需要计算连接在一起的陆地（岛屿）数量，而上下左右这种才算连接在一起，对角线和反对角线上的元素不算。例如下图算三个岛屿：
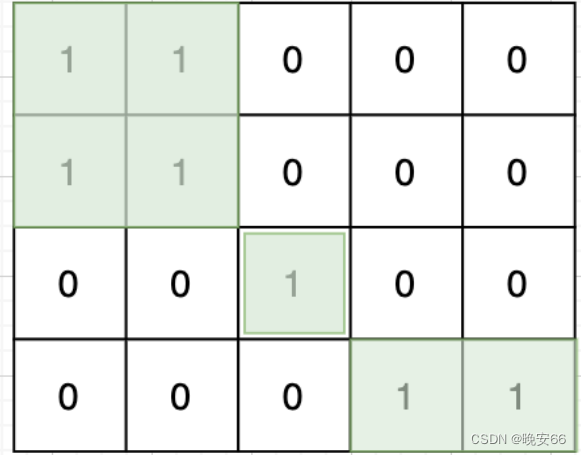
在这里插入图片描述

  基本思路是遇到一个没有遍历过的陆地，计数器++，然后把该节点陆地连接的陆地全部标记上。遇到标记过的陆地节点和海洋节点全部跳过，最终计数器就是岛屿的数量。因为要标价节点是否遍历过，所以我们创建一个visited布尔数组，false代表未遍历过，true代表遍历过。遍历二维数组采用两个for循环。节点的连接节点遍历通过偏移量数组delta_x_y。终止条件和越界参数处理的if语句相同。

  程序如下：

// 200、岛屿数量-深度优先搜索
class Solution {
private:int result = 0;vector<vector<int>> delta_x_y = { {0, -1}, {0, 1}, {-1, 0}, {1, 0} };	// 上下左右四个方向的偏移量void dfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {	// 1、递归输入参数// 3、单层递归逻辑for (int i = 0; i < 4; i++) {int nextx = x + delta_x_y[i][0];int nexty = y + delta_x_y[i][1];if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 越界了，直接跳过 2、终止条件if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') { // 没有访问过的，同时是陆地的visited[nextx][nexty] = true;dfs(grid, visited, nextx, nexty);}}		}
public:int numIslands(vector<vector<char>>& grid) {vector<vector<bool>> visited = vector<vector<bool>>(grid.size(), vector<bool>(grid[0].size(), false));	// 遍历过的坐标for (int i = 0; i < grid.size(); i++) {	// 遍历行for (int j = 0; j < grid[0].size(); j++) {	// 遍历列if (!visited[i][j] && grid[i][j] == '1') {visited[i][j] = true;	// 遍历的陆地标记改为trueresult++;		// 遇到没访问过的陆地，岛屿数量++dfs(grid, visited, i, j);	// 深度优先搜索，将连接的陆地都标记上true}}}return result;}
};

复杂度分析：

  • 时间复杂度： O ( m × n ) O(m \times n) O(m×n)，其中 m m m和 n n n分别是岛屿数组的行数和列数。
  • 空间复杂度： O ( m × n ) O(m \times n) O(m×n)，主要是栈的调用，最坏情况下，网格全是陆地，深度优先搜索的深度达到 m × n m \times n m×n。

1.2 广度优先搜索BFS

  思路分析：广度优先搜索是一圈一圈的搜索过程，而模拟这样的搜索过程可以用队列来实现。每当我们将坐标加入队列时，就代表该左边已经遍历过了，将visited数组标记为true。
  程序如下：

// 200、岛屿数量-广度优先搜索
class Solution2 {
private:int result = 0;vector<vector<int>> delta_x_y = { {0, -1}, {0, 1}, {-1, 0}, {1, 0} };	// 上下左右四个方向的偏移量void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {queue<pair<int, int>> que; // 定义队列，队列中的元素是对组 pair<int, int>que.push({ x, y }); // 起始节点加入队列visited[x][y] = true; // 只要加入队列，立刻标记为访问过的节点while (!que.empty()) { // 开始遍历队列里的元素pair<int, int> cur = que.front(); que.pop(); // 从队列取元素int curx = cur.first;int cury = cur.second; // 当前节点坐标for (int i = 0; i < 4; i++) { // 开始想当前节点的四个方向左右上下去遍历int nextx = curx + delta_x_y[i][0]; int nexty = cury + delta_x_y[i][1]; // 获取周边四个方向的坐标if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 坐标越界了，直接跳过if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') { // 如果节点没被访问过que.push({ nextx, nexty });  // 队列添加该节点为下一轮要遍历的节点visited[nextx][nexty] = true; // 只要加入队列立刻标记，避免重复访问}}}}
public:int numIslands(vector<vector<char>>& grid) {vector<vector<bool>> visited = vector<vector<bool>>(grid.size(), vector<bool>(grid[0].size(), false));	// 遍历过的坐标for (int i = 0; i < grid.size(); i++) {	// 遍历行for (int j = 0; j < grid[0].size(); j++) {	// 遍历列if (!visited[i][j] && grid[i][j] == '1') {visited[i][j] = true;	// 遍历的陆地标记改为trueresult++;		// 遇到没访问过的陆地，岛屿数量++bfs(grid, visited, i, j);	// 深度优先搜索，将连接的陆地都标记上true}}}return result;}
};

复杂度分析：

  • 时间复杂度： O ( m × n ) O(m \times n) O(m×n)，其中 m m m和 n n n分别是岛屿数组的行数和列数。
  • 空间复杂度： O ( m i n ( m , n ) ) O(min(m, n)) O(min(m,n))，在最坏情况下，整个网格均为陆地，队列的大小可以达到 m i n ( m , n ) min(m, n) min(m,n)。

二、695、岛屿的最大面积

在这里插入图片描述

2.1 深度优先搜索DFS

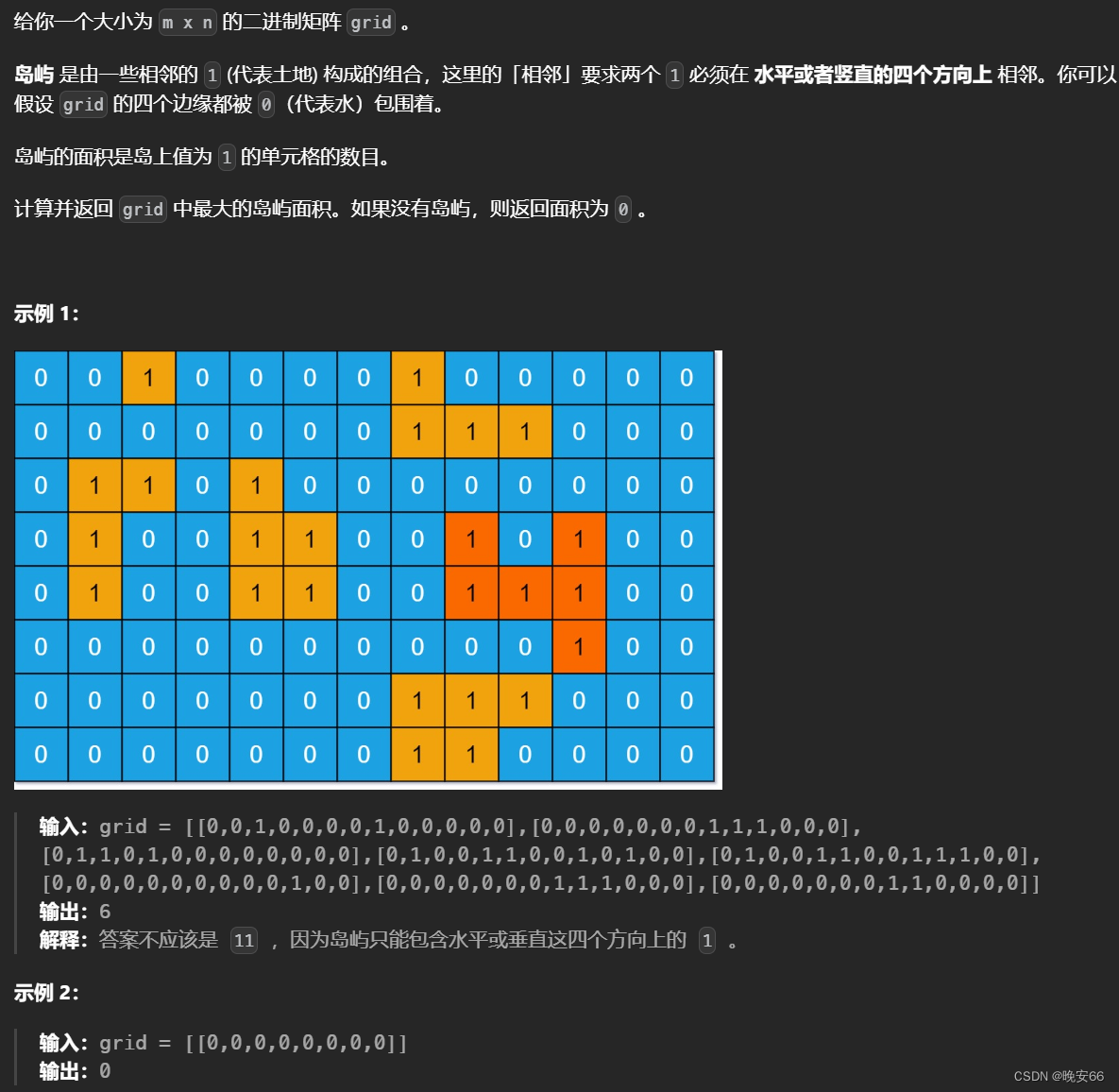
  思路分析：在200题岛屿数量的基础之上，题目要求我们求岛屿的最大面积，单块陆地的面积为1。思路很简单，每次遍历之后面积计数器++，然后在不同陆地的面积之中取最大值。
  程序如下：

// 695、岛屿的最大面积-深度优先搜索
class Solution3 {
private:int maxArea = 0;int Area = 0;vector<vector<int>> delta_x_y = { {0, -1}, {0, 1}, {-1, 0}, {1, 0} };	// 上下左右四个方向的偏移量void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {	// 1、递归输入参数// 2、终止条件 访问过或者遇到海水if (visited[x][y] || grid[x][y] == 0) return;	visited[x][y] = true;Area++;// 3、单层递归逻辑for (int i = 0; i < 4; i++) {int nextx = x + delta_x_y[i][0];int nexty = y + delta_x_y[i][1];if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 越界了，直接跳过 dfs(grid, visited, nextx, nexty);}}
public:int maxAreaOfIsland(vector<vector<int>>& grid) {vector<vector<bool>> visited = vector<vector<bool>>(grid.size(), vector<bool>(grid[0].size(), false));	// 遍历过的坐标for (int i = 0; i < grid.size(); i++) {	// 遍历行for (int j = 0; j < grid[0].size(); j++) {	// 遍历列if (!visited[i][j] && grid[i][j] == 1) {Area = 0;dfs(grid, visited, i, j);	// 深度优先搜索，将连接的陆地都标记上truemaxArea = max(Area, maxArea);					}}}return maxArea;}
};
  • 时间复杂度： O ( m × n ) O(m \times n) O(m×n)，其中 m m m和 n n n分别是岛屿数组的行数和列数。
  • 空间复杂度： O ( m × n ) O(m \times n) O(m×n)，主要是栈的调用，最坏情况下，网格全是陆地，深度优先搜索的深度达到 m × n m \times n m×n。

2.2 广度优先搜索BFS

  思路分析：思路和深度优先搜索一样。
  程序如下：

// 695、岛屿的最大面积-广度优先搜索
class Solution4 {
private:int maxArea = 0;int Area = 0;vector<vector<int>> delta_x_y = { {0, -1}, {0, 1}, {-1, 0}, {1, 0} };	// 上下左右四个方向的偏移量void bfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {queue<pair<int, int>> que; // 定义队列，队列中的元素是对组 pair<int, int>que.push({ x, y }); // 起始节点加入队列visited[x][y] = true; // 只要加入队列，立刻标记为访问过的节点Area++;while (!que.empty()) { // 开始遍历队列里的元素pair<int, int> cur = que.front(); que.pop(); // 从队列取元素int curx = cur.first;int cury = cur.second; // 当前节点坐标for (int i = 0; i < 4; i++) { // 开始想当前节点的四个方向左右上下去遍历int nextx = curx + delta_x_y[i][0];int nexty = cury + delta_x_y[i][1]; // 获取周边四个方向的坐标if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 坐标越界了，直接跳过if (!visited[nextx][nexty] && grid[nextx][nexty] == 1) { // 如果节点没被访问过que.push({ nextx, nexty });  // 队列添加该节点为下一轮要遍历的节点visited[nextx][nexty] = true; // 只要加入队列立刻标记，避免重复访问Area++;}}}}
public:int maxAreaOfIsland(vector<vector<int>>& grid) {vector<vector<bool>> visited = vector<vector<bool>>(grid.size(), vector<bool>(grid[0].size(), false));	// 遍历过的坐标for (int i = 0; i < grid.size(); i++) {	// 遍历行for (int j = 0; j < grid[0].size(); j++) {	// 遍历列if (!visited[i][j] && grid[i][j] == 1) {Area = 0;bfs(grid, visited, i, j);	// 深度优先搜索，将连接的陆地都标记上truemaxArea = max(Area, maxArea);}}}return maxArea;}
};

复杂度分析：

  • 时间复杂度： O ( m × n ) O(m \times n) O(m×n)，其中 m m m和 n n n分别是岛屿数组的行数和列数。
  • 空间复杂度： O ( m i n ( m , n ) ) O(min(m, n)) O(min(m,n))，在最坏情况下，整个网格均为陆地，队列的大小可以达到 m i n ( m , n ) min(m, n) min(m,n)。

三、完整代码

# include <iostream>
# include <vector>
# include <queue>
using namespace std;// 200、岛屿数量-深度优先搜索
class Solution {
private:int result = 0;vector<vector<int>> delta_x_y = { {0, -1}, {0, 1}, {-1, 0}, {1, 0} };	// 上下左右四个方向的偏移量void dfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {	// 1、递归输入参数// 3、单层递归逻辑for (int i = 0; i < 4; i++) {int nextx = x + delta_x_y[i][0];int nexty = y + delta_x_y[i][1];if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 越界了，直接跳过 2、终止条件if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') { // 没有访问过的，同时是陆地的visited[nextx][nexty] = true;dfs(grid, visited, nextx, nexty);}}		}
public:int numIslands(vector<vector<char>>& grid) {vector<vector<bool>> visited = vector<vector<bool>>(grid.size(), vector<bool>(grid[0].size(), false));	// 遍历过的坐标for (int i = 0; i < grid.size(); i++) {	// 遍历行for (int j = 0; j < grid[0].size(); j++) {	// 遍历列if (!visited[i][j] && grid[i][j] == '1') {visited[i][j] = true;	// 遍历的陆地标记改为trueresult++;		// 遇到没访问过的陆地，岛屿数量++dfs(grid, visited, i, j);	// 深度优先搜索，将连接的陆地都标记上true}}}return result;}
};// 200、岛屿数量-广度优先搜索
class Solution2 {
private:int result = 0;vector<vector<int>> delta_x_y = { {0, -1}, {0, 1}, {-1, 0}, {1, 0} };	// 上下左右四个方向的偏移量void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {queue<pair<int, int>> que; // 定义队列，队列中的元素是对组 pair<int, int>que.push({ x, y }); // 起始节点加入队列visited[x][y] = true; // 只要加入队列，立刻标记为访问过的节点while (!que.empty()) { // 开始遍历队列里的元素pair<int, int> cur = que.front(); que.pop(); // 从队列取元素int curx = cur.first;int cury = cur.second; // 当前节点坐标for (int i = 0; i < 4; i++) { // 开始想当前节点的四个方向左右上下去遍历int nextx = curx + delta_x_y[i][0]; int nexty = cury + delta_x_y[i][1]; // 获取周边四个方向的坐标if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 坐标越界了，直接跳过if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') { // 如果节点没被访问过que.push({ nextx, nexty });  // 队列添加该节点为下一轮要遍历的节点visited[nextx][nexty] = true; // 只要加入队列立刻标记，避免重复访问}}}}
public:int numIslands(vector<vector<char>>& grid) {vector<vector<bool>> visited = vector<vector<bool>>(grid.size(), vector<bool>(grid[0].size(), false));	// 遍历过的坐标for (int i = 0; i < grid.size(); i++) {	// 遍历行for (int j = 0; j < grid[0].size(); j++) {	// 遍历列if (!visited[i][j] && grid[i][j] == '1') {visited[i][j] = true;	// 遍历的陆地标记改为trueresult++;		// 遇到没访问过的陆地，岛屿数量++bfs(grid, visited, i, j);	// 深度优先搜索，将连接的陆地都标记上true}}}return result;}
};// 695、岛屿的最大面积-深度优先搜索
class Solution3 {
private:int maxArea = 0;int Area = 0;vector<vector<int>> delta_x_y = { {0, -1}, {0, 1}, {-1, 0}, {1, 0} };	// 上下左右四个方向的偏移量void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {	// 1、递归输入参数// 2、终止条件 访问过或者遇到海水if (visited[x][y] || grid[x][y] == 0) return;	visited[x][y] = true;Area++;// 3、单层递归逻辑for (int i = 0; i < 4; i++) {int nextx = x + delta_x_y[i][0];int nexty = y + delta_x_y[i][1];if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 越界了，直接跳过 dfs(grid, visited, nextx, nexty);}}
public:int maxAreaOfIsland(vector<vector<int>>& grid) {vector<vector<bool>> visited = vector<vector<bool>>(grid.size(), vector<bool>(grid[0].size(), false));	// 遍历过的坐标for (int i = 0; i < grid.size(); i++) {	// 遍历行for (int j = 0; j < grid[0].size(); j++) {	// 遍历列if (!visited[i][j] && grid[i][j] == 1) {Area = 0;dfs(grid, visited, i, j);	// 深度优先搜索，将连接的陆地都标记上truemaxArea = max(Area, maxArea);					}}}return maxArea;}
};// 695、岛屿的最大面积-广度优先搜索
class Solution4 {
private:int maxArea = 0;int Area = 0;vector<vector<int>> delta_x_y = { {0, -1}, {0, 1}, {-1, 0}, {1, 0} };	// 上下左右四个方向的偏移量void bfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {queue<pair<int, int>> que; // 定义队列，队列中的元素是对组 pair<int, int>que.push({ x, y }); // 起始节点加入队列visited[x][y] = true; // 只要加入队列，立刻标记为访问过的节点Area++;while (!que.empty()) { // 开始遍历队列里的元素pair<int, int> cur = que.front(); que.pop(); // 从队列取元素int curx = cur.first;int cury = cur.second; // 当前节点坐标for (int i = 0; i < 4; i++) { // 开始想当前节点的四个方向左右上下去遍历int nextx = curx + delta_x_y[i][0];int nexty = cury + delta_x_y[i][1]; // 获取周边四个方向的坐标if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 坐标越界了，直接跳过if (!visited[nextx][nexty] && grid[nextx][nexty] == 1) { // 如果节点没被访问过que.push({ nextx, nexty });  // 队列添加该节点为下一轮要遍历的节点visited[nextx][nexty] = true; // 只要加入队列立刻标记，避免重复访问Area++;}}}}
public:int maxAreaOfIsland(vector<vector<int>>& grid) {vector<vector<bool>> visited = vector<vector<bool>>(grid.size(), vector<bool>(grid[0].size(), false));	// 遍历过的坐标for (int i = 0; i < grid.size(); i++) {	// 遍历行for (int j = 0; j < grid[0].size(); j++) {	// 遍历列if (!visited[i][j] && grid[i][j] == 1) {Area = 0;bfs(grid, visited, i, j);	// 深度优先搜索，将连接的陆地都标记上truemaxArea = max(Area, maxArea);}}}return maxArea;}
};int main() {// // 200、岛屿数量测试案例//vector<vector<char>> grid = { {'1', '1', '1', '1', '0'} ,{'1', '1', '0', '1', '0'}, {'1', '1', '0', '0', '0'}, {'0', '0', '0', '0', '0'} };	//Solution s1;//int result = s1.numIslands(grid);// 695、岛屿的最大面积测试案例vector<vector<int>> grid = { {0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0}, { 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0 }, { 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0 }, { 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0 }, { 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0 }, { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0 }, { 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0 }, { 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0 } };Solution4 s1;int result = s1.maxAreaOfIsland(grid);cout << result << endl;system("pause");return 0;
}

end

这篇关于【算法与数据结构】200、695、LeetCode岛屿数量（深搜+广搜） 岛屿的最大面积的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/734883。

相关文章

openCV中KNN算法的实现

openCV中KNN算法的实现

《openCV中KNN算法的实现》KNN算法是一种简单且常用的分类算法,本文主要介绍了openCV中KNN算法的实现,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的... 目录KNN算法流程使用OpenCV实现KNNOpenCV 是一个开源的跨平台计算机视觉库，它提供了各
阅读更多...
springboot+dubbo实现时间轮算法

springboot+dubbo实现时间轮算法

《springboot+dubbo实现时间轮算法》时间轮是一种高效利用线程资源进行批量化调度的算法,本文主要介绍了springboot+dubbo实现时间轮算法,文中通过示例代码介绍的非常详细,对大家... 目录前言一、参数说明二、具体实现1、HashedwheelTimer2、createWheel3、n
阅读更多...
C#数据结构之字符串(string)详解

C#数据结构之字符串(string)详解

《C#数据结构之字符串(string)详解》：本文主要介绍C#数据结构之字符串(string),具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录转义字符序列字符串的创建字符串的声明null字符串与空字符串重复单字符字符串的构造字符串的属性和常用方法属性常用方法总结摘
阅读更多...
SpringBoot实现MD5加盐算法的示例代码

SpringBoot实现MD5加盐算法的示例代码

《SpringBoot实现MD5加盐算法的示例代码》加盐算法是一种用于增强密码安全性的技术,本文主要介绍了SpringBoot实现MD5加盐算法的示例代码,文中通过示例代码介绍的非常详细,对大家的学习... 目录一、什么是加盐算法二、如何实现加盐算法2.1 加盐算法代码实现2.2 注册页面中进行密码加盐2.
阅读更多...
Java时间轮调度算法的代码实现

Java时间轮调度算法的代码实现

《Java时间轮调度算法的代码实现》时间轮是一种高效的定时调度算法,主要用于管理延时任务或周期性任务,它通过一个环形数组（时间轮）和指针来实现,将大量定时任务分摊到固定的时间槽中,极大地降低了时间复杂... 目录1、简述2、时间轮的原理3. 时间轮的实现步骤3.1 定义时间槽3.2 定义时间轮3.3 使用时
阅读更多...
如何通过Golang的container/list实现LRU缓存算法

如何通过Golang的container/list实现LRU缓存算法

《如何通过Golang的container/list实现LRU缓存算法》文章介绍了Go语言中container/list包实现的双向链表,并探讨了如何使用链表实现LRU缓存,LRU缓存通过维护一个双向... 目录力扣：146. LRU 缓存主要结构 List 和 Element常用方法1. 初始化链表2.
阅读更多...
golang字符串匹配算法解读

golang字符串匹配算法解读

《golang字符串匹配算法解读》文章介绍了字符串匹配算法的原理,特别是Knuth-Morris-Pratt（KMP）算法,该算法通过构建模式串的前缀表来减少匹配时的不必要的字符比较,从而提高效率,在... 目录简介KMP实现代码总结简介字符串匹配算法主要用于在一个较长的文本串中查找一个较短的字符串（称为
阅读更多...
通俗易懂的Java常见限流算法具体实现

通俗易懂的Java常见限流算法具体实现

《通俗易懂的Java常见限流算法具体实现》：本文主要介绍Java常见限流算法具体实现的相关资料,包括漏桶算法、令牌桶算法、Nginx限流和Redis+Lua限流的实现原理和具体步骤,并比较了它们的... 目录一、漏桶算法1.漏桶算法的思想和原理2.具体实现二、令牌桶算法1.令牌桶算法流程:2.具体实现2.1
阅读更多...
Go语言中三种容器类型的数据结构详解

Go语言中三种容器类型的数据结构详解

《Go语言中三种容器类型的数据结构详解》在Go语言中,有三种主要的容器类型用于存储和操作集合数据：本文主要介绍三者的使用与区别,感兴趣的小伙伴可以跟随小编一起学习一下... 目录基本概念1. 数组（Array）2. 切片（Slice）3. 映射（Map）对比总结注意事项基本概念在 Go 语言中，有三种主要
阅读更多...
Python中的随机森林算法与实战

Python中的随机森林算法与实战

《Python中的随机森林算法与实战》本文详细介绍了随机森林算法,包括其原理、实现步骤、分类和回归案例,并讨论了其优点和缺点,通过面向对象编程实现了一个简单的随机森林模型,并应用于鸢尾花分类和波士顿房... 目录1、随机森林算法概述2、随机森林的原理3、实现步骤4、分类案例：使用随机森林预测鸢尾花品种4.1
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2