本文主要是介绍静态时序分析：SDC约束命令set_drive详解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
相关阅读
静态时序分析
https://blog.csdn.net/weixin_45791458/category_12567571.html
本章将讨论使用set_drive命令，它用于对输入端口的驱动能力建模。首先需要说明的是，默认情况下，DC在STA时默认输入端口的转换时间是0，这对于大多数情况来说过于理想。
set_drive命令设置了驱动端口的上拉/下拉电阻，因此电阻值越大，意味着驱动能力越弱；电阻值越小，意味着驱动能力越强。
该指令的BNF范式（有关BNF范式，可以参考以往文章）为：
set_drive resistance port_list[-rise] [-fall] [-min] [-max]//注：该命令的port_list参数一定要放在resistance参数后
指定电阻值
resistance是一个非负的电阻值，代表了驱动输入端口的单元的输出电阻，它的单位要与工艺库中指定的电阻单位一致。
指定端口列表
指定一个端口列表，包含输入端口或输入输出双向端口，如果有多于一个端口，需要使用引号或大括号包围。
简单使用
以图1所示的电路图为例，首先在输入端口clk定义一个时钟。
create_clock -period 10 [get_port clk]
图1 一个简单的例子
接着在输入端口d、c上分别定义两个输入延迟，参考时钟为clk。
set_input_delay 0.5 -clock clk [get_port d]
set_input_delay 0.5 -clock clk [get_port c]下面的set_drive命令在输入端口d上设置了驱动电阻。
set_drive 1 [get_port d]最后使用report_timing命令分别报告输入端口d、c到触发器的时序路径，记得使用-transition_time选项，结果如图2、图3所示。
图2 输入端口d的建立时间时序报告
图3 输入端口c的建立时间时序报告
从对比图4、图5可以看到，设置了驱动电阻的输入端口d的输入转换时间不再是0，而是0.001494，这实际上是电阻乘以输入端口电容（与输入端口连接的线网的总电容）的结果，可以使用report_net -significant_digits 7 [get_nets d]命
set_drive -rise 1 [get_port d]令查看输入端口d的电容，如图4所示。
图4 输入端口电容报告
同时我们可以发现，输入端口的驱动电阻同时带来了新的输入延迟（这个延迟虽然是外部延迟，但没有归为input external delay），延迟值同样是0.001494，计算方法与上面的转换时间一致。
指定上升、下降沿
-rise选项用于指定驱动作用于端口的上升沿、-fall选项用于指定驱动作用于端口的下降沿。如果这两个选项都没有指定，延迟同时作用于时钟的上升沿和下降沿（相当于它们同时指定）。
下面的命令指定了端口d的上升沿驱动电阻为1。
set_drive -rise 1 [get_port d]可以使用report_port -drive命令报告端口的驱动设置情况，如图5所示。
图5 端口驱动报告
从图中我们可以发现，上面的命令只设置了最大条件的输入端口d的上升沿驱动电阻，并没有设置最小条件，这个原因在下一节会说明。
指定最大最小、条件
-max选项用于指定驱动作用于最大条件（建立时间分析），-max选项用于指定驱动作用于最小条件（保持时间分析）。如果这两个选项都没有指定，延迟只作用于最大条件，这点和以前的很多命令不一样，需要特别注意。
下面的命令设置最小条件的输入端口d的上升沿驱动电阻为1，如图6所示。
set_drive -rise -min 1 [get_port d]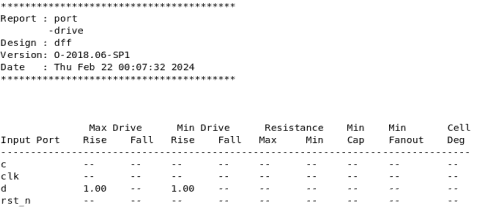
图6 端口驱动报告
写在最后
这个命令已经逐渐过时，不推荐使用，建议使用set_driving_cell命令或set_input_transition命令。
这篇关于静态时序分析：SDC约束命令set_drive详解的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
