本文主要是介绍【hoare基础版】快速排序算法(1),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
交换排序
QuickSort快速排序
Hoare整体思路
图解分析
Hoare版本代码
总代码
时间复杂度
交换排序
基本思想:所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。
QuickSort快速排序
快速排序:是Hoare于1962年提出的一种二叉树结构的交换排序方法。我们今天学习的就是基于Hoare思想的一种排序方式。
单趟基本思想(选取分界线位置keyi):
- 任取待排序元素序列中的某元素(最左边/最右边的数)作为基准值a[keyi]
- 按照该排序码将待排序集合分割成两子序列
- 左子序列中所有元素均小于基准值
- 右子序列中所有元素均大于基准值
整体基本思想:
- 然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
简单来说,整体思路是比较简单的,单趟基本思路有3中方式去实现:
- hoare版本1
- 挖坑版本2
- 前后指针版3
//有n个数----[0 , n-1]
//假设按照升序对array数组中[begin, end]区间中的元素进行排序0 n-1
void QuickSort(int array[], int begin, int end)
{//区间只有一个值/没有值(区间)返回if (begin >= end)return;// 按照keyi基准值对array数组的 [begin, end]区间中的元素进行划分// 有三种方式去找到keyi//PartSort1 PartSort2 PartSort3int keyi = PartSort1/2/3(array, begin, end);// 划分成功后以div为边界形成了左中右三部分//[begin, keyi-1] keyi [keyi+1, end)//keyi的位置的值 已经排好了// 递归排[begin, keyi-1]QuickSort(array, begin, keyi - 1);// 递归排[keyi+1, right]QuickSort(array, keyi + 1, end);
}上述为快速排序递归实现的主框架,发现与二叉树前序遍历规则非常像,大家在写递归框架时可想想二叉树前序遍历规则即可快速写出来,后序只需分析如何按照基准值来对区间中数据进行划分的方式即可。
Hoare整体思路
单趟基本思想(选取分界线位置keyi):
- 任取待排序元素序列中的某元素(最左边/最右边的数)作为基准值a[keyi]
- 按照该排序码将待排序集合分割成两子序列
- 左子序列中所有元素均小于基准值
- 右子序列中所有元素均大于基准值
- 目的:让keyi对应位置的值排到该排到的位置
值的设置
- 区间是[begin,end] (注意是下标)
选取关键字的下标keyi a[keyi]=key
设置两个下标用来值得比较:left right
循环放值
若left所对应的值小于<keyi所对应的值,符合要求,过掉
若left所对应的值大于>keyi所对应的值,不符合要求,停下
若right所对应的值大于>keyi所对应的值,符合要求,过掉
若right所对应的值小于<keyi所对应的值,不符合要求,停下
循环之后left 和 right找到各自符合的值,交换即可
把比a[keyi]小的值放到左边,比a[keyi]大的值放到右边
相遇中线
left和right相遇,停止循环
相遇的位置,即使中线位置
与a[keyi]交换即可,则a[keyi]放到该放到的位置,a[keyi]已经排好了
整体基本思想:
- 然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
- 返回条件
- 递归到只有一个元素的区间
- 没有元素的区间。
重点突破:
- left和right相遇的位置对应的数值总是比keyi所对应的值小
- 相遇的三种情况分析
- 选key值三种方式
- 直接选取最左边/右边
- 选取序列中的随机值key,和最左边/最右边的交换
- 三数取中法选key,和最左边/最右边的交换
易错点突破:
- 比较起始位置从begin // begin+1 (顺序结构)
- 相遇点的处理(错位)
- 等于=的问题
- 局部变量的问题
图解分析 
Hoare版本代码
// 0 n-1
int PartSort1(int* a, int begin, int end)//返回分割线
{int left = begin;int right = end;int keyi = begin;while (left < right){//找小while (left < right && a[right] >= a[keyi]){right--;}//找大while (left<right && a[left] <= a[keyi]){left++;}//找到了Swap(&a[right], &a[left]);}Swap(&a[left], &a[keyi]);keyi = left;return keyi;//分割 [begin,keyi-1] keyi [keyi+1,end]
}总代码
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void QuickSort(int* a, int begin,int end)
{if (begin >= end)//只有1个元素 没有区间{return;}int keyi = PartSort1(a, begin, end);QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}// 0 n-1
int PartSort1(int* a, int begin, int end)//返回分割线
{int left = begin;int right = end;int keyi = begin;while (left < right){//找小while (left < right && a[right] >= a[keyi]){right--;}//找大while (left<right && a[left] <= a[keyi]){left++;}//找到了Swap(&a[right], &a[left]);}Swap(&a[left], &a[keyi]);keyi = left;return keyi;//分割 [begin,keyi-1] keyi [keyi+1,end]
}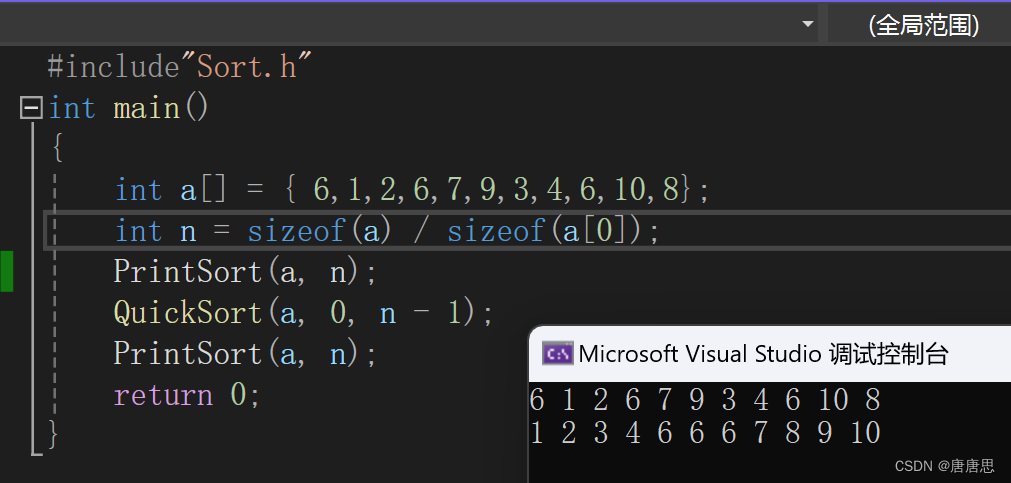
时间复杂度
- 最好情况:O(N*logN)
- 最坏情况:O(N^2)
- >>>>>>>>解决方法1:随机数选key
- >>>>>>>>解决方法2:三数取中选key
🙂感谢大家的阅读,若有错误和不足,欢迎指正。
这篇关于【hoare基础版】快速排序算法(1)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







