【halcon知识】：共生矩阵

本文主要是介绍【halcon知识】：共生矩阵，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、共生矩阵基本概念

二、以上看不懂吗？请看下面举例后再回头看就懂了

2.1 分级（scales）

2.2 求规定偏移的共生矩阵

2.2.1 水平偏移（度）

2.2.2 垂直方向的偏移（9度）

2.2.3 1-3象限方向的偏移（45度）

2.2.4 2-4象限方向的偏移（135度）

三、参考代码

3.1 原图：

3.2 锁定区域

3.3 求出共生矩阵代码

3.4 结果：

一、说明

共生矩阵是一种用于图像分析和特征提取的工具，常用于纹理分析。它是由二维灰度图像中像素对之间的空间关系和灰度级别共同定义的矩阵。共生矩阵可以描述图像中不同方向上像素之间的灰度值对比关系，并通过统计这些关系的频率来提取纹理特征。共生矩阵通常包括四个性质：方向、距离、灰度级和共生概率。

二、共生矩阵基本概念

共现矩阵或共现分布（也称为：灰度共现矩阵 GLCM）是在图像上定义为同时出现的像素值（灰度值或颜色）的分布的矩阵) 在给定的偏移量处。它被用作具有各种应用的纹理分析方法，特别是在医学图像分析中。

给定灰度图像 $I$ ，共生矩阵计算图像中具有特定值和偏移量组成一个偶对的像素对出现的频率（这是不是类似直方图？对的，就是二维图内两个相对位置像素序偶对的直方统计）。

灰度级别化（scales）：指灰度按照对数取划分等级，如0-255灰度可写成 $2^0-1\rightarrow 2^8-1$ ，共8个等级
偏移量： $(\Delta x,\Delta y)$ 是一个位置算子，可以应用于图像中的任何像素（忽略边缘效应）：例如， $(1,2)$ 可以表示“向下一格，向右两格”。

取图像(N×N)中任意一点（x，y）及偏离它的另一点（x+a，y+b），设该点序的灰度值为（g1，g2）和（g2，g1）。令点（x，y）在整个画面上移动，则会得到各种（g1，g2）和（g2，g1）值。

对于给定的偏移量，具有 $p$ 不同像素的图像将产生一个 $p\times p$ 维度的共现矩阵。
共现矩阵的 $(i,j)^{\text{th}}$ 值给出了图像中出现的次数 $i^{\text{th}}$ 和 $j^{\text{th}}$ 像素值出现在偏移量给出的关系中。

对于具有 $p$ 个不同像素值的图像， $p\times p$ 共现矩阵 C 定义在 $n\times m$ 图像 $I$ ，由偏移量 $(\Delta x,\Delta y)$ 参数化，如：

$C_{\Delta x,\Delta y}(i,j)=\sum _{x=1}^{n}\sum _{y=1}^{m}{\begin{cases}1,&{\text{if }}I(x,y)=i{\text{ and }}I(x+\Delta x,y+\Delta y)=j\\0,&{\text{otherwise}}\end{cases}}$

其中： $i$ 和 $j$ 是像素值； $x$ 和 $y$ 是图像 $I$ 中的空间位置；偏移量 $(\Delta x,\Delta y)$ 定义了计算该矩阵的空间关系； $I(x,y)$ 表示像素 $(x,y)$ 处的像素值。

对于8bit的图像，灰度共生矩阵为 $8\times 8$ 矩阵。

图像的“值”最初指的是指定像素的灰度值，但可以推广成任何值，从二进制开/关值到32位整数等等。（请注意，32位颜色将生成232×232共生矩阵！）

共现矩阵也可以根据距离 $d$ 和角度 ${\displaystyle\theta}$ 来参数化，而不是偏移量 $(\Delta x,\Delta y)$ 。

任何矩阵或矩阵对都可以用来生成共生矩阵，尽管它们最常见的应用是测量图像中的纹理，因此如上所述的典型定义假定矩阵是图像。

也可以跨两个不同的图像定义矩阵。这样的矩阵可以用于颜色映射。

三、以上看不懂吗？请看下面举例后再回头看就懂了

3.1 分级的图例

这里有 $3\times 3$ 的灰度图像，试看我们如何对灰度分级处理：

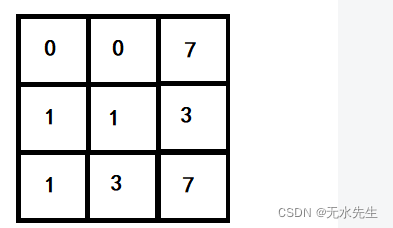
分级后（scales）

$0 = 2^0-1$ ; $\\1 = 2^1-1;$ $3=2^2-1;$ $7=2^3-1$ 因此，原图被分成四级，转化成：

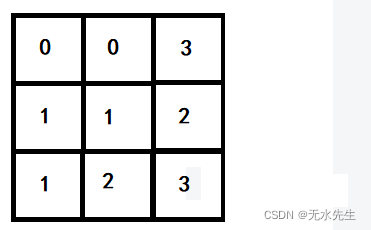
3.2 求规定偏移的共生矩阵

关于0，90，45，135度的偏移（向右向下为正方向）：

3.2.1 水平偏移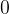（ $0$ 度）

$(\Delta x,\Delta y)}={\displaystyle (1,0)$

对 $\begin{Bmatrix} 0 & 0 &3 \\ 1& 1 & 2\\ 1& 2& 3 \end{Bmatrix}$ 的每个像素进行 $offset = {\displaystyle (\Delta x,\Delta y)}={\displaystyle (1,0)}$ 的偶对采集，如下：

（0，0），（0，0），（0，3），（3，0）

（1，1），（1，1），（1，2），（2，1）

（1，2），（2，1），（2，3），（3，2）

统计以上偶对，形成下表：

	0	1	2	3
0	2	0	0	1
1	0	2	2	0
2	0	2	0	1
3	1	0	1	0

这就是 $offset = {\displaystyle (\Delta x,\Delta y)}={\displaystyle (1,0)}$ 的共生矩阵：

$\begin{Bmatrix} 2 & 0 & 0& 1\\ 0 & 2&2& 0\\ 0& 2& 0&1 \\ 1&0 & 1& 0\end{Bmatrix}$

3.2.2 垂直方向的偏移（9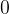 $0$ 度）

$(\Delta x,\Delta y)}={\displaystyle (0,1)$

对 $\begin{Bmatrix} 0 & 0 &3 \\ 1& 1 & 2\\ 1& 2& 3 \end{Bmatrix}$ 的每个像素进行 $offset = {\displaystyle (\Delta x,\Delta y)}={\displaystyle (0,1)}$ 的偶对采集，如下：

（0，1），（1，0），（1，1），（1，1）

（0，1），（1，0），（1，2），（2，1）

（3，2），（2，3），（2，3），（3，2）

统计以上偶对，形成下表：

	0	1	2	3
0	0	2	0	0
1	2	2	1	0
2	0	1	0	2
3	0	0	2	0

$\begin{Bmatrix} 0 & 2 & 0& 0\\ 2 & 2&1& 0\\ 1& 2& 0&2 \\ 0&0 & 2& 0\end{Bmatrix}$

3.2.3 1-3象限方向的偏移（45度）

$(\Delta x,\Delta y)}={\displaystyle ( 1,-1)$ （此处表示向下一格，向右-1格，别搞错了！）

对 $\begin{Bmatrix} 0 & 0 &3 \\ 1& 1 & 2\\ 1& 2& 3 \end{Bmatrix}$ 的每个像素进行 $offset = {\displaystyle (\Delta x,\Delta y)}={\displaystyle (1,-1)}$ 的偶对采集，如下：

（1，1），（1，1），（2，2），（2，2）

（1，0），（0，1），（1，3），（3，1）

统计以上偶对，形成下表：

	0	1	2	3
0	0	1	0	0
1	1	2	0	1
2	0	0	2	0
3	0	1	0	0

$\begin{Bmatrix} 0 & 1 & 0& 0\\ 1 & 2&0& 1\\ 0& 0& 2&0 \\ 0&1 & 0& 0\end{Bmatrix}$

2.2.4 2-4象限方向的偏移（135度）

$(\Delta x,\Delta y)}={\displaystyle ( 1,1)$

对 $\begin{Bmatrix} 0 & 0 &3 \\ 1& 1 & 2\\ 1& 2& 3 \end{Bmatrix}$ 的每个像素进行 $offset = {\displaystyle (\Delta x,\Delta y)}={\displaystyle (1,1)}$ 的偶对采集，如下：

（0，1），（1，0），（0，2），（2，0）

（1，2），（2，1），（1，3），（3，1）

统计以上偶对，形成下表：

	0	1	2	3
0	0	1	1	0
1	1	0	1	1
2	1	1	0	0
3	0	1	0	0

$\begin{Bmatrix} 0 & 1 & 1& 0\\ 1 & 0&1& 1\\ 1& 1& 0&0 \\ 0&1 & 0& 0\end{Bmatrix}$

至此，图像的四个方向共生矩阵都求出了。

四、参考代码

以下代码求两个区域的共生矩阵，并用热图打印出来。

4.1 原图：

4.2 锁定区域

4.3 求出共生矩阵代码

* Calculate the co-occurrence matrices of two regions in an image
* 
read_image (Image, 'mreut')
dev_close_window ()
get_image_size (Image, Width, Height)
dev_open_window (0, 0, Width, Height, 'black', WindowID)
dev_display (Image)
dev_set_draw ('margin')
* Create two rectangles parallel to the coordinate axes
gen_rectangle1 (Rectangle1, 350, 100, 450, 200)
gen_rectangle1 (Rectangle2, 100, 200, 200, 300)
* set look-up-table of the output window
dev_set_lut ('temperature')
gen_cooc_matrix (Rectangle1, Image, Matrix1, 6, 0)
gen_cooc_matrix (Rectangle2, Image, Matrix2, 6, 0)
dev_set_lut ('default')