本文主要是介绍天上掉下来的FFT,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
FFT
本文学习借鉴 Link 董晓算法
说实话董老师讲的太好了
前言
闲来无事,点了一下随机跳题。
LUOGU 4461 [CQOI2018] 九连环
读完题随便一写, O ( n ) O(n) O(n) 的转移(当时很激动,毕竟以为秒了紫题)。反手一交 30 p t s 30pts 30pts 仔细一看,这题居然没有让去模!?!(开始发癫。
FFT 前置芝士
虚数的意义
我们将坐标系上的点可以这样理解:
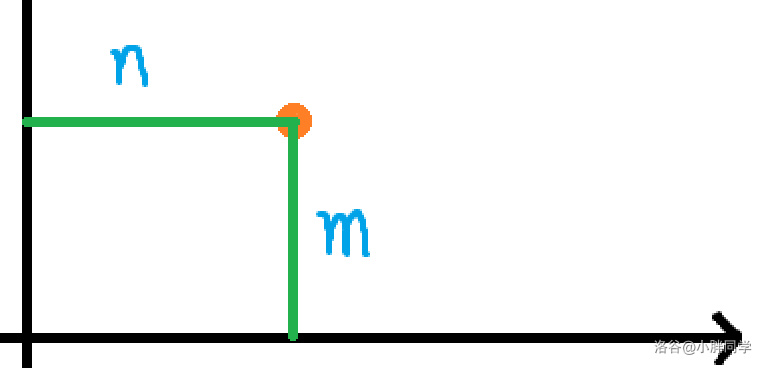
将 n n n 看作实部 m m m 看作虚部,即点 A = n + i m A = n + im A=n+im 。
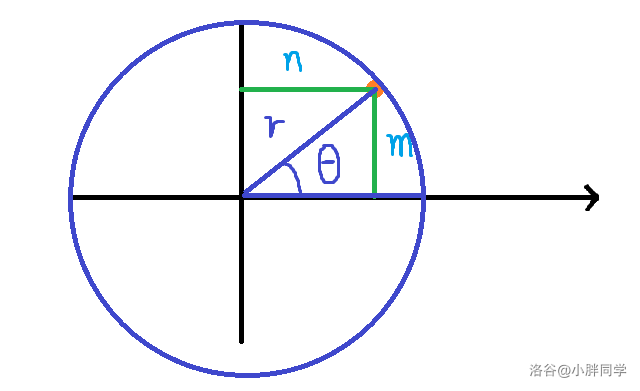
呢我们就可以用半径和角度表示一个圆上的点。
如点 A = cos θ ⋅ r + i ⋅ sin θ ⋅ r A = \cos \theta \cdot r + i \cdot \sin \theta \cdot r A=cosθ⋅r+i⋅sinθ⋅r
则利用 π \pi π 来表示角度,钦定将圆分成 n n n 份这个角度占 k k k 份,再钦定 r = 1 r = 1 r=1 就出现了一个神奇的表示:
单位根 ω n k = cos 2 π k n + i ⋅ sin 2 π k n \omega ^ k _ n = \cos \frac {2 \pi k} {n} + i \cdot \sin \frac {2 \pi k}{n} ωnk=cosn2πk+i⋅sinn2πk
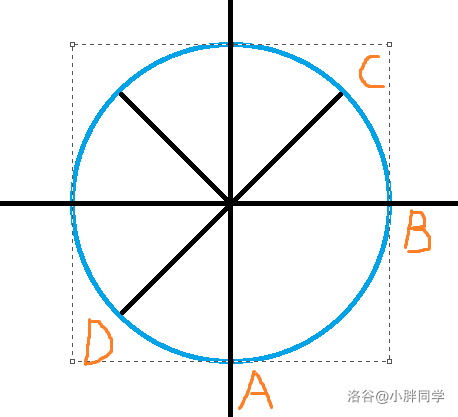
其有一些神奇且具象的性质:
周期性 : ω n k = ω n k + n \omega ^ {k} _ {n} = \omega ^ {k + n} _ {n} ωnk=ωnk+n
很好理解就是转一圈回到原点.
对称性 : ω n k + n 2 = − ω n k \omega ^ {k + \frac{n}{2}} _ {n} = - \omega ^ {k} _ {n} ωnk+2n=−ωnk
形如上图点 C 和点 D,转了 180 度相当于原数取反.
折半性 : ω 2 n 2 k = ω n k \omega ^ {2k} _ {2n} = \omega ^ {k} _ {n} ω2n2k=ωnk
相当于分子分母化简,也很好理解 你在分成 8 份时取 4 份和在 4 份中去 2 份意义相同.
虚数乘
设 A = a 1 + i ⋅ a 2 , B = b 1 + i ⋅ b 2 A = a_1 + i \cdot a_2 , B = b_1 + i \cdot b_2 A=a1+i⋅a2,B=b1+i⋅b2
A × B = ( a 1 + i ⋅ a 2 ) × ( b 1 + i ⋅ b 2 ) A \times B = ( a_1 + i \cdot a_2 ) \times(b_1 + i \cdot b_2) A×B=(a1+i⋅a2)×(b1+i⋅b2)
= a 1 b 1 + i 2 a 2 b 2 + i ( a 2 b 1 + a 1 b 2 ) = a_1b_1 + i^2a_2b_2 + i(a_2b_1 + a_1b_2) =a1b1+i2a2b2+i(a2b1+a1b2)
= a 1 b 1 − a 2 b 2 + i ( a 2 b 1 + a 1 b 2 ) = a_1b_1 - a_2b_2 + i(a_2b_1 + a_1b_2) =a1b1−a2b2+i(a2b1+a1b2)
开始正题
众所周知 , 一个 n n n 阶多项式可以用 n n n 个点来唯一确定.
对于长度为 n n n 的多项式
A ( x ) = a 1 + a 2 x + a 3 x 2 ⋯ a n + 1 x n A(x) = a_1 + a_2x + a_3x^2 \cdots a_{n+ 1}x^n A(x)=a1+a2x+a3x2⋯an+1xn
我们可以间其奇数次幂和偶数次幂分离(别问为什么这样做,我感觉 FFT 的思路就是天上掉下来的)
奇数次幂 : ( a 1 x + a 3 x 3 ⋯ a n − 1 x n − 2 ) = ( a 2 + a 4 x 2 ⋯ a n x n ) ⋅ x (a_1x + a_3x^3 \cdots a_{n - 1}x^{n - 2}) = (a_2 + a_4x^2 \cdots a_{n}x^{n}) \cdot x (a1x+a3x3⋯an−1xn−2)=(a2+a4x2⋯anxn)⋅x
偶数次幂 : ( a 0 + a 2 x 2 ⋯ a n − 2 x n − 2 ) (a_0 + a_2x^2 \cdots a_{n - 2}x^{n - 2}) (a0+a2x2⋯an−2xn−2)
设:
A 1 ( x ) = ( a 0 + a 2 x 2 ⋯ a n − 2 x n 2 − 1 ) A_1(x) = (a_0 + a_2x^2 \cdots a_{n - 2}x^{\frac n 2 - 1}) A1(x)=(a0+a2x2⋯an−2x2n−1)
A 2 ( x ) = ( a 1 + a 3 x 2 ⋯ a n − 1 x n 2 − 1 ) A_2(x) = (a_1 + a_3x^2 \cdots a_{n - 1}x^{\frac n 2 -1}) A2(x)=(a1+a3x2⋯an−1x2n−1)
A ( x ) = A 1 ( x 2 ) + A 2 ( x 2 ) ⋅ x A(x) = A_1(x ^ 2) + A_2(x ^ 2) \cdot x A(x)=A1(x2)+A2(x2)⋅x
用前面的单位根往里带(评价为天上掉下来的)
图片来自董老师 Link 董晓算法

发现如果 n = 2 k n = 2 ^ k n=2k 就可以直接二分到底,所有我们钦定 n = 2 k n = 2 ^ k n=2k .
可以直接递归到底然后再反推回来.
我们就可以得到 n 个点
求出 多项式 A 和 B 把每个点乘起来,再把单位根的倒数带入将点值转话为 z i = a i ⋅ n z_i = a_i \cdot n zi=ai⋅n
图片来自董老师 Link 董晓算法

所有 a i = z i n a_i = \frac {z_i} n ai=nzi 就得到答案了!
优化
递归显然是不优雅的
我们观察最终搜索到的序列,
图片来自董老师 Link 董晓算法

观察发现每个数字的结果其实就是将原数的二进制倒过来
称之为蝴蝶变化.
这时候 zxc 大佬就要开始发癫了
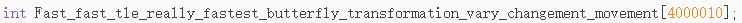
如何求呢?
观察发现 f[i] = f[i / 2] / 2 + [i & 1] * n / 2;
所有我们就可以 O ( n ) O(n) O(n) 推出变化 O ( n log n ) O(n \log n) O(nlogn) 得到答案.
这篇关于天上掉下来的FFT的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




