本文主要是介绍代码随想录算法训练营第三十六天|435. 无重叠区间 763.划分字母区间 56. 合并区间,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
435. 无重叠区间
链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
细节:
1. 这道题目和 452.用最少数量的箭引爆气球 ,452中的弓箭数量其实就是 无重叠区间的数量,用总的区间数减去 无重叠区间的数量 就是我们要移除的元素数量。
所以得出方法一:使用总区间数减去无重叠区间的数量
这个方法是根据左边界进行排序,记录弓箭的数量,其实就是在记录 无重叠区间的数量,那么总的区间的数量减去无重叠区间的数量就是要移除的区间的数量
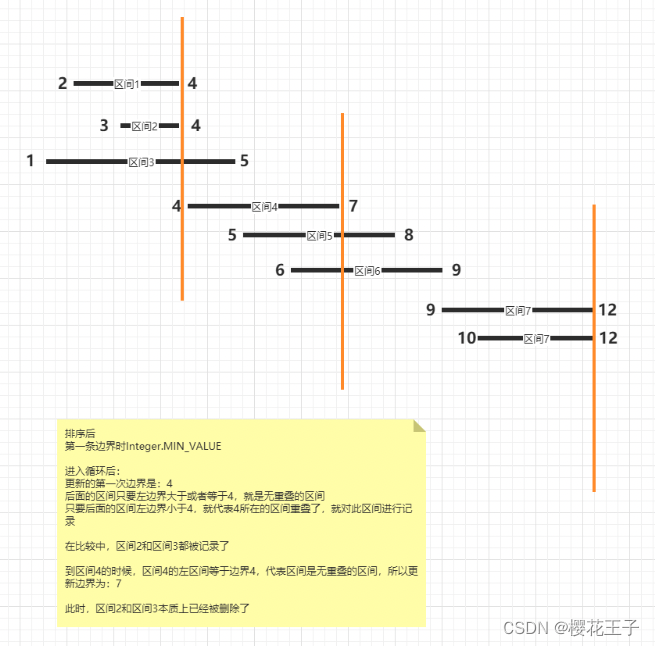
2. 还有一种思路是根据右边界进行排序
如果本区间的左区间大于或者等于上一个区间的右边界,就说明是 无重叠的区间 ,此时需要更新最新的 无重叠右边界。
如果本区间的左区间小于上一个区间的右边界,说明 区间重叠了,是要删除的区间,就进行记录
所以得出了方法二:根据右区间进行排序,记录重叠区间的数量
这个方法根据右边界进行排序,不断记录重叠区间的数量,如果遇到不重叠的区间,就对重叠边界的条件进行改变
无重叠区间
根据左边界排序,使用总区间数减去无重叠区间的数量
class Solution {public int eraseOverlapIntervals(int[][] intervals) {Arrays.sort(intervals, (a, b) -> {return Integer.compare(a[0], b[0]);});int count = 1;for (int i = 1; i < intervals.length; i++){if (intervals[i][0] >=intervals[i - 1][1] ){count++;}else{intervals[i][1] = Math.min(intervals[i][1], intervals[i - 1][1]);}}return intervals.length - count;}
}根据右边界排序,记录重叠区间的数量
class Solution {public int eraseOverlapIntervals(int[][] intervals) {Arrays.sort(intervals,(a,b) -> {// 按照区间右边界升序排序return a[1] - b[1];});int count = 0;int edge = Integer.MIN_VALUE;for (int i = 0; i < intervals.length; i++) {// 如果一个区间的右边界小于当前区间的左边界,说明无交集if (intervals[i][0] >= edge) {edge = intervals[i][1];} else {count++;}}return count;}
}763.划分字母区间
链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
细节:
在遍历的过程中相当于是要找每一个字母的边界,如果找到之前遍历过的所有字母的最远边界,说明这个边界就是分割点了。此时前面出现过所有字母,最远也就到这个边界了
1、首先统计每一个字符最后出现的位置
2、从头遍历字符,并更新字符的最远出现下标,如果找到字符最远出现位置下标和当前下标相等了,则找到了分割点直接在字符串上进行切割的话,切割点是原字符串的坐标,比如结果应该是[9,7,8],最后的结果确是[9,16,24],想出现这种情况的时候,应该想到使用滑动窗口
直接在字符串上操作滑动窗口的话,执行时间比较长,所以将字符串转换成数组进行滑动窗口的操作会更快
划分字母区间
使用边界的思路写判断条件看不懂这个思路就看下面滑动窗口的思路,比较明显class Solution {public List<Integer> partitionLabels(String s) {List<Integer> list = new LinkedList<>();int[] edge = new int[26];char[] chars = s.toCharArray();for ( int i = 0; i < chars.length; i++) {edge[chars[i] - 'a'] = i;}int index = 0;int last = -1;for (int i = 0; i < chars.length; i++) {index = Math.max(index,edge[chars[i] - 'a']);if (i == index) {list.add(i - last);last = i;}}return list;}
}
使用滑动窗口的思路写判断条件(直接在字符串上进行滑动)
class Solution {public List<Integer> partitionLabels(String s) {// 结果集List<Integer> result = new LinkedList<>();// 统计每个字符出现的最后下标int[] edge = new int[26];char[] chars = s.toCharArray();for ( int i = 0; i < chars.length; i++) {edge[chars[i] - 'a'] = i;}// 滑动窗口int left = 0;int right = 0;for (int i = 0; i < chars.length; i++) {// 找出字符出现的最远位置right = Math.max(right,edge[chars[i] - 'a']);// 当遍历到最远最远位置的下标的时候,就说明该裁剪了if (i == right) {result.add(right - left + 1);left = right + 1;}}return result;}
}
使用滑动窗口的思路写判断条件(直接在字符串上进行滑动)
class Solution {public List<Integer> partitionLabels(String s) {// 结果集List<Integer> result = new LinkedList<>();// 滑动窗口int left = 0;int right = 0;for (int i = 0; i < s.length(); i++) {// 找出当前字符的最远边界right = Math.max(right,s.lastIndexOf(s.charAt(i)));// 如果到达边界,就进行移动和记录if (right == i) {result.add(right - left + 1);left = right + 1;}}return result;}
}
56. 合并区间
链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
细节:
这几道重叠区间的问题做下来,对重叠区间的问题有了一定的感觉
首先要了解清楚题意是要干什么,然后再选择正确的排序,这是成功的开始
然后再根据排序进行一定的操作,是计数还是合并,还是删除……重叠区间的思路并不难,难得是对代码的驾驭程度
重叠区间的题目总结:
452.用最少数量的箭引爆气球 求的是不重叠的区间数量,与 435 形成对比。(计数,不用构建新数组)
435.无重叠区间 求得是删除几个区间就可以使数组形成无重叠区间,与 452 对比》(计数,不用构建新数组)
763.划分字母区间 求得是分割字符串,这道题目更像是滑动窗口,但是也是不断判断某个最大区间内的内容
56.合并区间 前面的几道题目做出来之后,就会对这道题目很有感觉了,就是一些代码的细节上需要多加注意。(构建新数组,需要借助结合,这一点和 406.根据身高重建队列 比较相似)
class Solution {public int[][] merge(int[][] intervals) {// 将区间按照从小到大的顺序进行排列Arrays.sort(intervals,(a,b) -> Integer.compare(a[0],b[0]));// 使用一个linkedList集合便于重建数组LinkedList<int[]> result = new LinkedList<>();int left = intervals[0][0];int right = intervals[0][1];// 遍历排序后的数组,如果数组重叠就进行合并for (int i = 1; i < intervals.length; i++) {if (intervals[i][0] > right) {// 这种情况区间不重叠,收集结果result.add(new int[]{left,right});// 重新定义下一个区间的左右left = intervals[i][0];right = intervals[i][1];} else {// 这种情况区间重叠了。更新右边界right = Math.max(intervals[i][1],right);}}// 最后剩余一个区间再添加到集合中result.add(new int[]{left,right});// 将结果集转换成数组进行输出return result.toArray(new int[result.size()][]);}
}这篇关于代码随想录算法训练营第三十六天|435. 无重叠区间 763.划分字母区间 56. 合并区间的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!