经典白话算法之中缀表达式和后缀表达式

本文主要是介绍经典白话算法之中缀表达式和后缀表达式，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、后缀表达式求值

后缀表达式也叫逆波兰表达式，其求值过程可以用到栈来辅助存储。

假定待求值的后缀表达式为：6 5 2 3 + 8 * + 3 + *，则其求值过程如下：

（1）遍历表达式，遇到的数字首先放入栈中，依次读入6 5 2 3 此时栈如下所示：

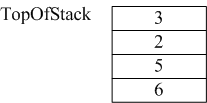
（2）接着读到“+”，则从栈中弹出3和2，执行3+2，计算结果等于5，并将5压入到栈中。

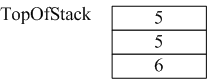
（3）然后读到8（数字入栈），将其直接放入栈中。

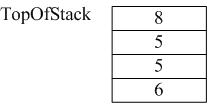
（4）读到“*”，弹出8和5，执行8*5，并将结果40压入栈中。

而后过程类似，读到“+”，将40和5弹出，将40+5的结果45压入栈...以此类推。最后求的值288。

代码：

[cpp]  view plain copy  
 #include<iostream>  
 #include<stack>  
 #include<stdio.h>  
 #include<string.h>  
 using namespace std;  
   
 int main(){  
     string PostArray;  
     int len,i,a,b;  
     while(cin>>PostArray){  
         stack<int> Stack;  
         len = PostArray.length();  
         for(i = 0;i < len;i++){  
             //跳过空格  
             if(PostArray[i] == ' '){  
                 continue;  
             }  
             //如果是数字则入栈  
             if(PostArray[i] >= '0' && PostArray[i] <= '9'){  
                 Stack.push(PostArray[i] - '0');  
             }  
             //如果是字符则从栈读出两个数进行运算  
             else{  
                 //算数a出栈  
                 a = Stack.top();  
                 Stack.pop();  
                 //算法b出栈  
                 b = Stack.top();  
                 Stack.pop();  
                 //进行运算（+ - * /）  
                 if(PostArray[i] == '+'){  
                     Stack.push(a + b);  
                 }  
                 else if(PostArray[i] == '-'){  
                     Stack.push(a - b);  
                 }  
                 else if(PostArray[i] == '*'){  
                     Stack.push(a * b);  
                 }  
                 else if(PostArray[i] == '/'){  
                     Stack.push(a / b);  
                 }  
             }  
         }//for  
         printf("%d\n",Stack.top());  
     }//while  
     return 0;  
 }  