本文主要是介绍[算法系列之十六]数据压缩之游程编码,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
简介
无论现在计算机和网络的速度有多快,用户始终要求更快速的体验。为了降低传输数据的容量,我们通常会对数据进行压缩。这就是计算机科学领域一直是研究和发展的焦点的原因。
数据压缩算法有很多,有些是无损的,有些是有损的,但是它们的主要目标都是降低存储空间和传输量。对于两个远距离节点之间的数据传输,这些压缩算法非常有用。也许最直观的例子就是web服务器和浏览器之间的数据传输。
在过去的几年里做了很多关于文件压缩的研究,这些研究基于客户端实现的。这样的文件有javascript、css、html和图像。实际上,服务器和客户端都具备一些数据压缩技术,例如GZIP的使用极大地降低了数据传输量。此外,还有很多的工具和技巧能够降低数据大小。
事实上,当文件在客户的虚拟机上执行时,程序员不必理会文件的具体格式如何。如此一来空格、水平制表符和换行符对于文件上下文的理解没有任何意义。这就是YUI Compressor、Google Closure Compiler等压缩工具移除那些符号的原因。当然,为了提高压缩率文件还能被进一步压缩。本篇文章暂不讨论这一点,但这表明了数据压缩算法的重要性。
如果我们使用一些数据压缩工具,效果会更好。不幸的是,事实并非如此,压缩率通常取决于数据本身。很明显,数据压缩算法的选择主要取决于数据,我们必须首先对数据进行研究。
这里我将讨论“游程编码”(run-length encoding),它是一种十分简单的无损数据压缩算法,在某些情况下非常有用。
概述
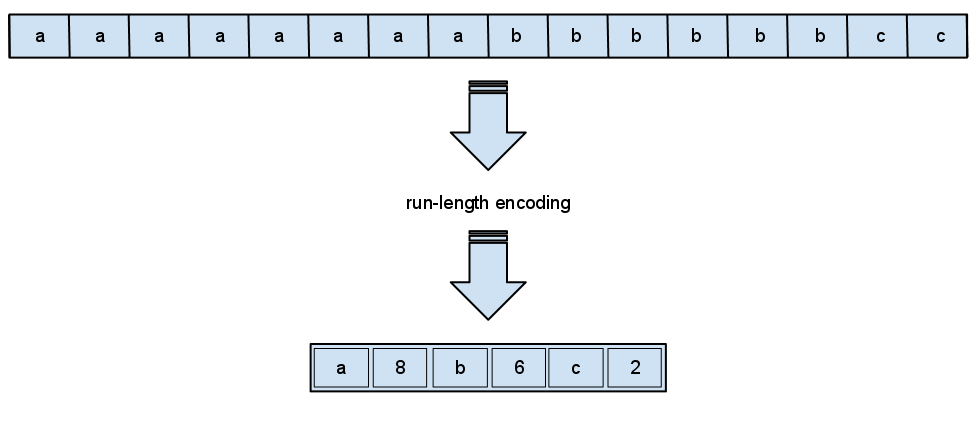
该算法的实现是用当前数据元素以及该元素连续出现的次数来取代字符串中连续出现的数据部分。具体实现我们通过一个字符串实例来说明。
aaaaaaaaaabbbaxxxxyyyzyx
字符串长度为24,我们可以看到字符串中有很多的重复部分。使用游程算法,我们用较短的字符串后加一个计数值来替换游程对象。
a10b3a1x4y3z1y1x1
此时字符串长度为17,大约是初始字符串长度的70%。很明显,这并不是压缩给定字符串的最佳方式。例如当字符仅出现一次时,我们并不需要其后添加“1”。在某些情况下,这种方式会增加初始字符串的长度,而这违反了我们的初衷。这样我们得到的字符串如下。
a10b3ax4y3zyx
此时字符串长度为13,是初始长度的54%!上面例子的一个变种是不对字符保持计数,而是对位置进行计数。这样原始字符串可以被压缩成下面这样。
a0b10a13x14y18z21y22x23
使用这两种方式中的哪一个取决于我们的目标。第二种情况下,我们能够实现二分查找的优化。
显然,这个算法不仅适用于字符串。对数组也能取得很好的结果。一个典型的例子是服务器和客户机之间字符对象(JSON)的传输。特别是如果有大量重复数据序列的存在,我们能获取很好的压缩结果。
实现
下面的实现是假设我们要使用c++(原文使用PHP实现)编写程序对字符串进行压缩。但是这个算法本质上并没有限制我们只能压缩字符串。正如我前面所说,只要略微修改,我们就能将其用于其他数据结构。游程算法适用于大量重复元素序列非常重要,不管是字符元素还是数组元素。
/*--------------------------------
* 日期:2015-02-07
* 作者:SJF0115
* 题目: 数据压缩之Run-Length Encoding
* 博客:
------------------------------------*/
#include <iostream>
using namespace std;string RunLengthEncoding(string str){int size = str.size();if(size <= 0){return "";}//ifchar pre = ' ';string result;int count = 0;for(int i = 0;i < size;++i){if(str[i] != pre){if(i > 0){result += to_string(count);}//ifresult += str[i];count = 0;pre = str[i];}//if++count;}//forresult += to_string(count);return result;
}int main(){//string str("aaaaaaaaaabbbaxxxxyyzyx");//string str("abbbb");string str("a");string result = RunLengthEncoding(str);cout<<"压缩后数据->"<<result<<endl;return 0;
}
或者
/*--------------------------------
* 日期:2015-02-07
* 作者:SJF0115
* 题目: 数据压缩之Run-Length Encoding
* 博客:
------------------------------------*/
string RunLengthEncoding(string str){int size = str.size();if(size <= 0){return "";}//ifstring result(str.substr(0,1));int count = 0;for(int i = 0;i < size;++i){if(i > 0 && str[i] != str[i-1]){result += to_string(count);result += str[i];count = 0;}//if++count;}//forresult += to_string(count);return result;
}略微优化。
/*--------------------------------
* 日期:2015-02-07
* 作者:SJF0115
* 题目: 数据压缩之Run-Length Encoding
* 博客:
------------------------------------*/
string RunLengthEncoding(string str){int size = str.size();if(size <= 0){return "";}//ifstring result(str.substr(0,1));int count = 0;for(int i = 0;i < size;++i){if(i > 0 && str[i] != str[i-1]){if(count > 1){result += to_string(count);}//ifresult += str[i];count = 0;}//if++count;}//forif(count > 1){result += to_string(count);}//ifreturn result;
}aaaaaaaaaabbbaxxxxyyzyx ----> a10b3ax4y2zyx
最后一个小变化——现在我们存储字符位置。
/*--------------------------------
* 日期:2015-02-07
* 作者:SJF0115
* 题目: 数据压缩之Run-Length Encoding
* 博客:
------------------------------------*/
string RunLengthEncoding(string str){int size = str.size();if(size <= 0){return "";}//ifstring result;for(int i = 0;i < size;++i){if(i == 0){result += str[i]+to_string(i);}//ifelse if(i > 0 && str[i] != str[i-1]){result += str[i] + to_string(i);}//if}//forreturn result;
}aaaaaaaaaabbbaxxxxyyzyx ----> a0b10a13x14y18z20y21x22
复杂性和数据压缩
我们习惯使用时间复杂度来衡量时间,通常希望能找到最快的实现方式,比如查找算法。在这里快速压缩数据并不特别重要,重要的是尽可能的无损压缩,使得输出尽可能的小。游程编码的优点在于该算法容易实现。
应用程序
在很多情况下,我们可以使用游程编码。它常用于图像压缩,特别是用于黑白图片处理时是效果非常好。这里,我将介绍上面提及的另一种应用情况。假设我们要使用JSON将大量数组数据传给我们的Ajax程序。假设这些传输数据是一些年份,例如电影首映的年份。一年内有很多电影首映,虽然数据已被排序,但实际上我们没有得到任何好处。更要命的是有大量的数据序列。这里我们可以使用游程编码。
$data = array(0 => 1991,1 => 1991,...2223 => 1991,2224 => 1992,...19298 => 1995,19299 => 1996,...
);正如你看到的,传输整个数组将会是一个噩梦,特别是如果网络的速度很慢。最好对数据进行压缩(例如使用PHP的json_encode)。
// {"0":1991,"1":1991, ..., "2223":1991,"2224":1992, ..., "19298":1995,"19299":1996, ...}
echo json_encode($data);运行游程编码之后,我们得到结果像以下数组一样(注意这些只是样本数据,最佳存储数据格式取决于你)
$data = array(0 => array(1991, 2224),1 => array(1992, 3948),2 => array(1995, 2398),3 => array(1996, 3489),
);JSON输出
// [[1991,2224],[1992,3948],[1995,2398],[1996,3489]]
echo json_encode($data);注意如果是已排序数据,我们能够获得更好的压缩结果!!!这种方式能够用于图像,图形或者地图坐标的压缩。
这是数据压缩在日常工作中有用的唯一例子。尽管服务器和客户机之间的通信可以优化和压缩,我们能够改善它。换句话说我们不能够保证对方是否支持压缩。
那么,相应的客户端必须对数据进行解压,这个过程很缓慢。
在第一种情况下,我们只是用时间去传输,如下面的流程图所示。

未压缩数据传输时间!
第二种情况,我们应该累加压缩,传输和解压的时间。

压缩数据传输时间!
所有这些都很重要,但总的来说数据压缩在我们日常生活中的多数情况下都很方便。
原文链接
Computer Algorithms: Data Compression with Run-length Encoding
这篇关于[算法系列之十六]数据压缩之游程编码的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!