本文主要是介绍(AtCoder Beginner Contest 341)(A - D),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
比赛地址 :
Tasks - Toyota Programming Contest 2024#2(AtCoder Beginner Contest 341)
A . Print 341
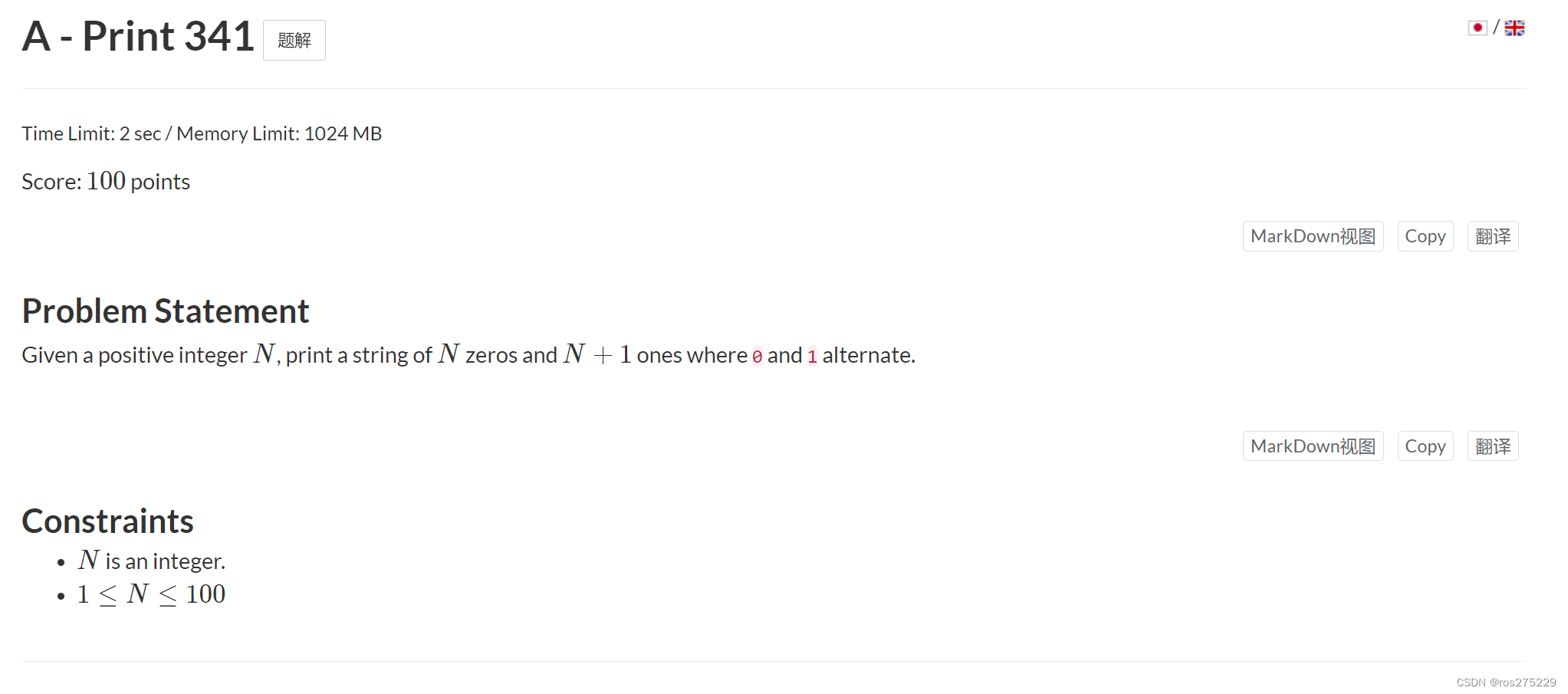
模拟就好了 , 先放一个 1 , 然后放 n 个 01 ;
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
#define lowbit(x) (x&(-x))
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define int long long
typedef long long LL;
const int mod = 1e9+7;
const int N = 2e5+10;using namespace std;inline void solve(){int n ; cin >> n ;cout << 1 ;for(int i=0;i<n;i++){cout << "01";}
}signed main()
{IOSint _ = 1;// cin >> _;while(_ --) solve();return 0;
}B . Foreign Exchange
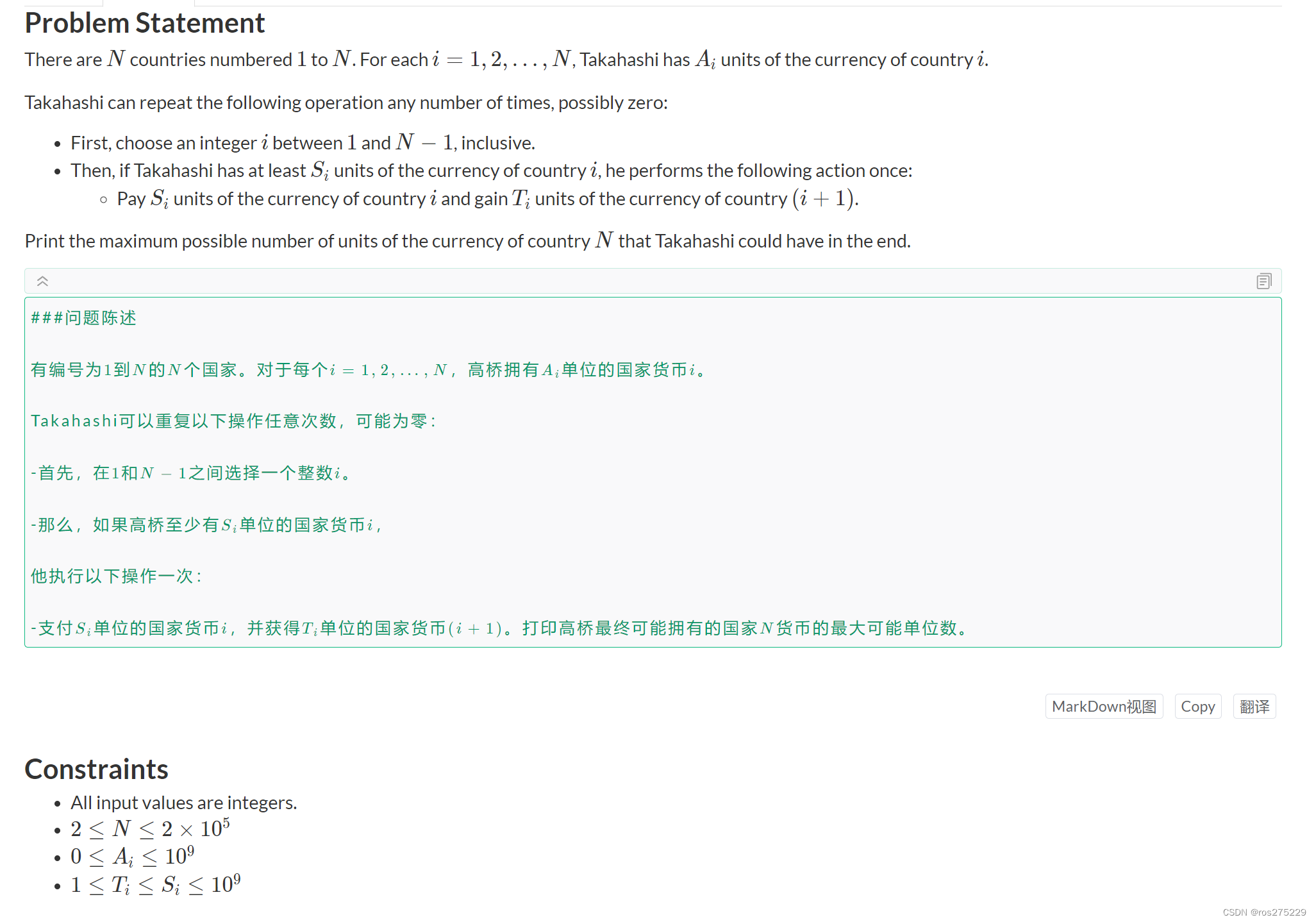
贪心, 因为后面操作不会影响前面的,前面的会使后面的变大,而题目要求使最后一个最大,那么 , 直接从前往后遍历就好了 ;
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
#define lowbit(x) (x&(-x))
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define int long long
typedef long long LL;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;using namespace std;inline void solve() {int n ; cin >> n ;vector<int> a(n+1) ,s(n) , t(n) ;for(int i=1;i<=n;i++) cin >> a[i] ;for(int i=1;i<n;i++) cin >> s[i] >> t[i] ;// 第i个-si ,i+1就+tifor(int i=1;i<n;i++){if(a[i] >= s[i]){int k = a[i] / s[i] ;a[i] -= k * s[i] ;a[i+1] += k * t[i] ; }}cout << a[n] << endl;
} signed main()
{IOSint _ = 1;// cin >> _;while (_--) solve();return 0;
}C . TaKahashi Gets Lost
暴力 , 对于每一个点,找它是否满足题意,如果满足,则ans++;
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
#define lowbit(x) (x&(-x))
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define int long long
typedef long long LL;
const int mod = 1e9+7;
const int N = 510;char c[N][N] ;using namespace std;inline void solve(){int h,w,n;cin>>h>>w>>n ;string t ; cin >> t ;for(int i=1;i<=h;i++){for(int j=1;j<=w;j++){cin >> c[i][j] ;}}int ans = 0 ;for(int i=1;i<=h;i++){for(int j=1;j<=w;j++){if(c[i][j]=='#') continue ;int a = i , b = j ;bool tag = true;for(int k=0;k<n;k++){if(t[k]=='L'){if(b==1){tag = false;break ; }b-=1;if(c[a][b]=='#'){tag = false;break;}}else if(t[k]=='U'){if(a==1){tag = false;break ; }a-=1;if(c[a][b]=='#'){tag = false;break;}}else if(t[k]=='R'){if(b==w){tag = false;break ; }b+=1;if(c[a][b]=='#'){tag = false;break;}}else{// "D"if(a==h){tag = false;break ; }a+=1;if(c[a][b]=='#'){tag = false;break;}}}if(tag){ans ++ ;}}}cout << ans << endl ;
}signed main()
{IOSint _ = 1;// cin >> _;while(_ --) solve();return 0;
}D . Only one of two
先找到n,m的最小公倍数l,那么对于一个数x,能被n整除且<=x的数的个数就是[x/n],所以可以得到下面式子(因为可能同时能被n,m整除,要删掉能被l整除的数字个数):
[x/n] + [x/m] - 2 * [x/l] >= k;
这样就可以使用二分来进行查找 ;
#include <bits/stdc++.h>
using namespace std;
typedef long long LL ;
LL gcd(LL a , LL b){return b ? gcd(b, a % b) : a;
}// 设 l 是 m,n的最小公倍数 int main() {long long n,m,x,k;cin>>n>>m>>k;x=(n*m)/gcd(n,m);// 求出最小公倍数 long long l=0,r=(long long)2e+18,mid,y;while((l+1)<r){// 二分查找 t/n+t/m-2*t/x>=k的最佳答案 mid=(l+r)/2;y=(mid/n)+(mid/m)-2*(mid/x);if(y<k)l=mid;else r=mid;}cout<<r<<endl;return 0;
}
这篇关于(AtCoder Beginner Contest 341)(A - D)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




